Dans les exercices d’évaluation de fin d’année, on retrouve la trigonométrie dans des questions dans les QCM notées chacune sur un point.
Remarque : en général, aucune justification n’est demandée.
Exercice n°1
Soit f la fonction définie sur \mathbf{R} par f(x)=cos(x)+x^2.
Parmi les propositions suivantes, laquelle est vraie ?
a) f est paire | b) f est impaire | c) f(x+2\pi)=f(x) | d) f(x+\pi)=-f(x) |
Exercice n°2
Dans l’intervalle ]-\pi;\pi] l’équation 2sin(x)-1=0 a pour solutions :
a) -\frac{\pi}{3} et \frac{\pi}{3} | b) \frac{\pi}{3} et \frac{2\pi}{3} | c) -\frac{\pi}{6} et \frac{\pi}{6} | d) \frac{\pi}{6} et \frac{5\pi}{6} |
Exercice n°3
Dans l’intervalle ]0;2\pi] l’équation 2cos(x)+\sqrt{2}=0 a pour solutions :
a) -\frac{\pi}{4} et \frac{\pi}{4} | b) \frac{\pi}{4} et \frac{3\pi}{4} | c) -\frac{3\pi}{4} et \frac{3\pi}{4} | d) \frac{3\pi}{4} et \frac{5\pi}{4} |
Exercice n°4
Le nombre réel -\frac{\pi}{4} est associé au même point sur le cercle trigonométrique que le réel :
a) -\frac{20\pi}{4} | b) \frac{23\pi}{4} | c) -\frac{22\pi}{4} | d) -\frac{21\pi}{4} |
Exercice n°5
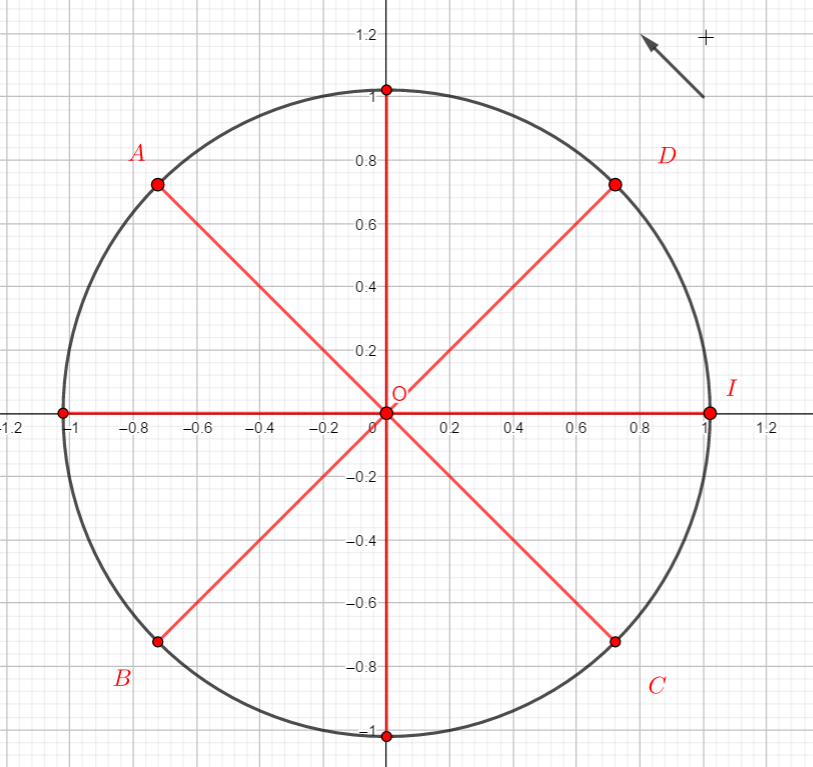
Le nombre réel \frac{16\pi}{3} a pour image sur le cercle trigonométrique le point :
a) A | b) B | c) C | d) D |
Exercice n°6
Le nombre réel x appartient à ]-\frac{\pi}{2};0] et cos(x)=0.8 :
a) sin(x)=0.2 | b) sin(x)=-0.2 | c) sin(x)=0.6 | d) sin(x)=-0.6 |
Exercice n°7
On considère l’équation sin(x)=-1 pour x réel.
a) Cette équation a une unique solution dans \mathbf{R} | b) Cette équation a une infinité de solutions dans \mathbf{R} | c) -\pi est la solution de cette équation. | d) -\pi+2k\pi sont les solutions de cette équation. |
Exercice n°8
Pour x réel, sin(35\pi+x) est égal à
a) sin(x) | b) -sin(x) | c) cos(x) | d) -cos(x) |
Exercice n°9
Pour x réel, cos(15\pi-x) est égal à
a) sin(x) | b) -sin(x) | c) cos(x) | d) -cos(x) |
Exercice n°10
Dans l’intervalle ]-\pi;\pi] l’équation sin(x)=\frac{\sqrt{3}}{2} a pour solutions :
a) -\frac{\pi}{3} et \frac{\pi}{3} | b) \frac{\pi}{3} et \frac{2\pi}{3} | c) -\frac{\pi}{3} et -\frac{2\pi}{3} | d) \frac{\pi}{6} et \frac{5\pi}{6} |
Exercice n°11
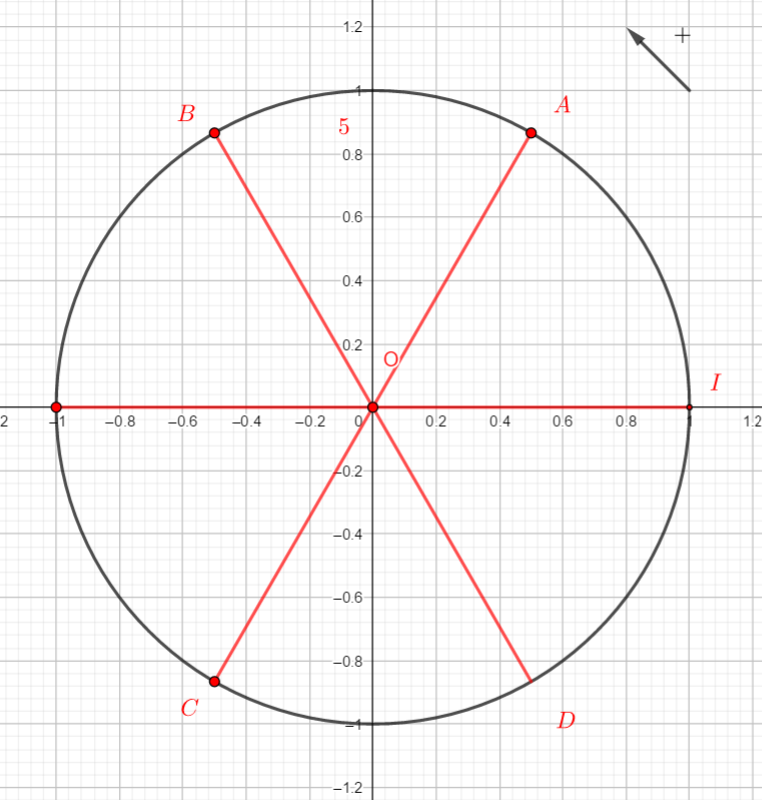
Le nombre réel \frac{35\pi}{4} a pour image sur le cercle trigonométrique le point :
a) A | b) B | c) C | d) D |