Exercice n°1
L’axe de symétrie de la parabole d’équation y=x^2-2x+6 est :
a) y=-x | b) x=1 | c) x=-1 | d) y=1 |
Exercice n°2
Soit f la fonction définie sur \mathbf{R} par f(x)=x^2-5x+6.
L’abscisse du minimum est :
a) 5 | b) \frac{5}{2} | c) -5 | d) \frac{6}{5} |
Exercice n°3
Quelle est la forme factorisée de f(x)=2(x-1)^2-18?
a) 2x^2-4x-16 | b) 2(x-10)(x+8) | c) 2(x+10)(x-8) | d) 2(x-4)(x+2) |
Exercice n°4
Soit a, b, c trois réels tels que a\ne 0 et soit f la
fonction définie sur \mathbf{R} par : f(x)=ax^2+bx+c
Soit \Deltason discriminant.
La représentation graphique de la fonction f dans un repère orthonormé est donnée ci-contre.
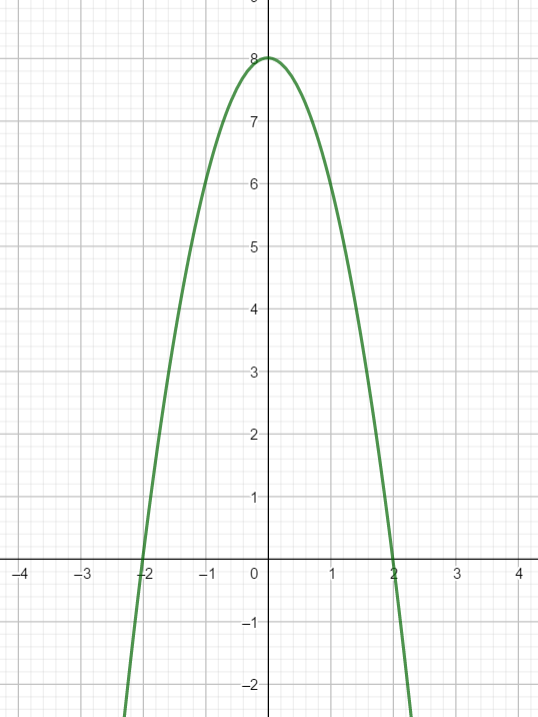
a) a>0 et \Delta>0 | b) a>0 et \Delta<0 | c) a<0 et \Delta>0 | d) a<0 et \Delta<0 |
Exercice n°5
L’inéquation x^2+x+1>0
a) n’a pas de solution. | b) a une seule solution | c) a pour solution [-1;1] | d) a pour solution l’ensemble \mathbf{R} |
Exercice n°6
L’inéquation x^2-3x+2>0 a pour ensemble solution :
a) ]-\infty;1[ \cup ]2;+\infty[ | b) ]-2;-1[ | c) ]1;2[ | d) ]-\infty;-2[ \cup ]-1;+\infty[ |
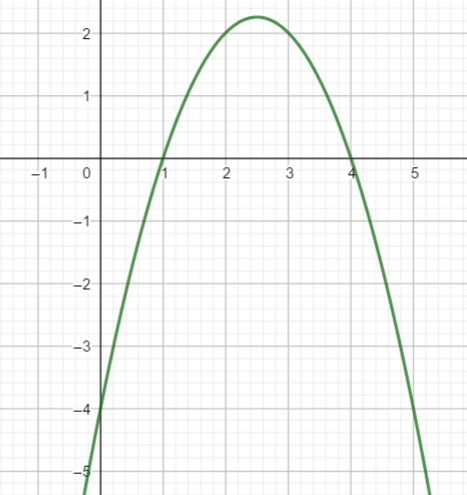
Exercice n°7
Soit f une fonction polynôme du second degré dont la courbe représentative dans un repère orthonormé est donnée ci-contre.
Une expression de f(x) est :
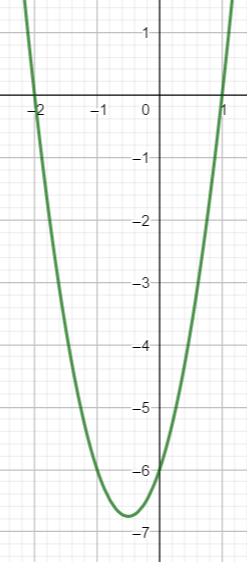
a) x^2+x-2 | b) 3x^2-6 | c) 3x^2+3x-6 | d) 2x^2+2x+6 |
Exercice n°8
On considère la fonction définie sur \mathbf{R} par f(x)=2x^2+2x-4. On admet que l’une des quatre courbes ci-dessous représente la fonction f. Laquelle ?
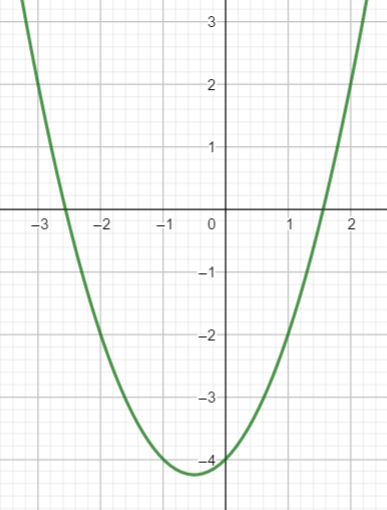
Réponse a
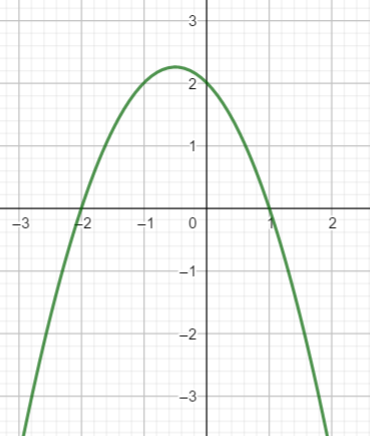
Réponse b
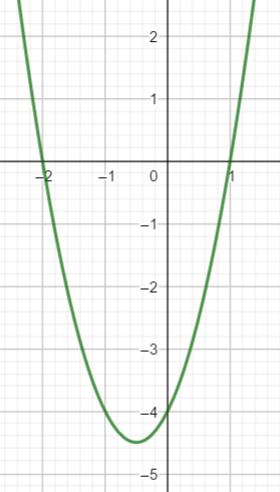
Réponse c
Réponse d
Exercice n°9
Soit f une fonction polynôme du second degré dont la courbe représentative dans un repère orthonormé est donnée ci-contre.
Une expression factorisée de f(x) est :
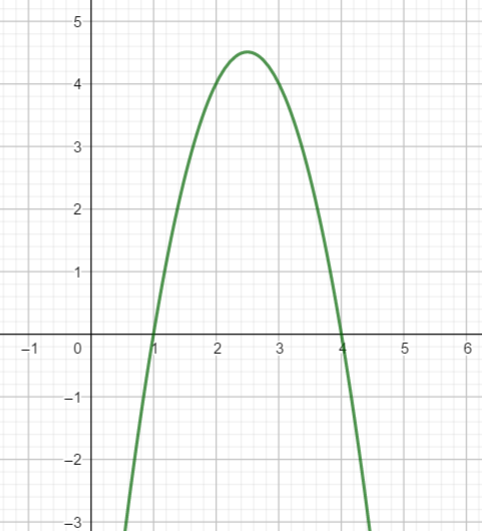
a) 2(x-1)(x-4) | b) 2(x+1)(x+4) | c) -2(x-1)(x-4) | d) -2(x+1)(x+4) |
Exercice n°10
L’équation x^2=8x-7
a) n’a pas de solution. | b) a une seule solution 8 | c) a pour solution S=\{-7;-1\} | d) a pour solution S=\{1;7\} |



