Quelques rappels de seconde
Exemple n°1 (fonctions en Python et boucles bornées)
On veut calculer des termes de la suite définie par récurrence, u_0=1 et u_{n+1}=2u_n.
Voici une fonction Python qui va calculer le terme de la suite de notre choix.
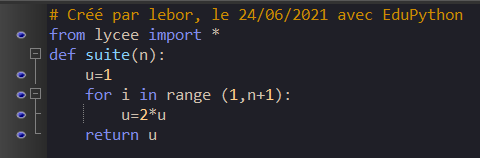
Quelques commentaires :
On crée une fonction que l’on nomme suite. On rappelle que le nom de la fonction est toujours suivi de parenthèses. Ici on rajoute un paramètre dans les parenthèses, c’est une variable que la fonction a besoin de connaître pour pouvoir s’exécuter. Ici cela correspond au rang du terme de la suite qu’on veut déterminer.
On a choisit range (1, n+1) , cela signifie que i prend les valeurs de 1 à (n+1)-1 c’est-à-dire de 1 à n.
Le mot-clé return a deux rôles : stopper l’exécution de la fonction et indiquer la valeur à renvoyer par la fonction.
Question : quelle valeur est renvoyée par la fonction si on écrit suite(4) dans la console ?
Exemple n°2 (fonctions en Python et boucles non bornées)
On veut déterminer à partir de quel rang, les termes de la suite définie par, u_0=2 et u_{n+1}=3u_n-1 deviennent supérieurs ou égaux à 10000.
Voici une fonction Python qui va calculer le terme de la suite de notre choix.
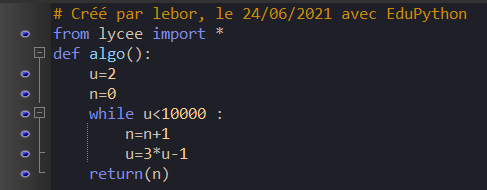
Commentaire :
On crée une fonction que l’on nomme algo. On rappelle que le nom de la fonction est toujours suivi de parenthèses. Ici on ne rajoute pas de paramètre.
Question : quelle valeur est renvoyée par la fonction ?
Exemple n°3 (fonctions)
On veut calculer des termes de la suite définie par formule explicite u_{n}=n^2-2n+1.
Voici une fonction Python qui va calculer le terme de la suite de notre choix.

Quelques commentaires :
On crée une fonction que l’on nomme encore suite.
On rappelle que n^2 se code n**2.
Question : quelle valeur est renvoyée par la fonction si on écrit suite(3) dans la console ?
Exemple n°4 (fonctions et instruction conditionnelle)
On veut déterminer si deux vecteurs \overrightarrow{u} et \overrightarrow{v} sont orthogonaux en calculant leur produit scalaire.
Voici un programme Python qui va calculer le produit scalaire et le comparer à zéro.
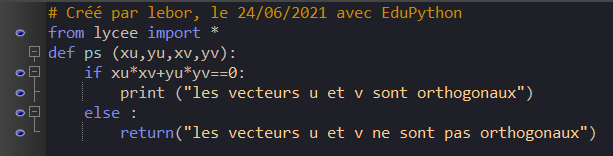
Quelques commentaires :
On crée une fonction que l’on nomme ps.
On utilise la strucure conditionnelle suivante : la condition if…else (“si…sinon”)
On rappelle que pour tester une égalité, on utilise le symbole ==.
Question : quelle valeur est renvoyée par la fonction si on écrit ps (2,3,6,-4) dans la console ?
Exemple n°5 (fonctions et instruction conditionnelle)
On veut résoudre une équation du second degré
Voici un programme Python qui va calculer \Delta…
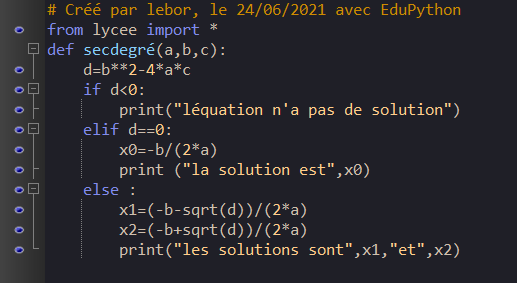
Quelques commentaires :
On crée une fonction que l’on nomme secdegré.
On utilise la structure conditionnelle suivante : la condition if…elif…else (“si…sinon si… sinon”).
On rappelle que pour tester une égalité, on utilise le symbole ==.
Question : quelle valeur est renvoyée par la fonction si on écrit secdegré (1,2,1) dans la console ?



