Exercice n°1
Voici un programme écrit en langage Python.
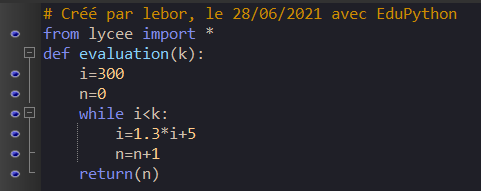
Parmi les phrases qu’on pourrait lire dans la console Python, laquelle est vraie ?
a)>>>évaluation(500) 1 | b)>>>évaluation(500) 2 | c)>>>évaluation(500) 3 | d)>>>évaluation(500) 1 |
Exercice n°2
On considère l’algorithme suivant, écrit en langage usuel :
Suite(N)
A\leftarrow 10
Pour k de 1 à N
A\leftarrow 3*A-10
Fin Pour
Renvoyer A
Pour N=4, la valeur renvoyée est
a) 140 | b) 410 | c) 4 | d) 1220 |
Exercice n°3
Soit (u_n) la suite définie par u_0=2 et par u_{n+1}=2u_n-3. On souhaite qu’à la fin de l’exécution de l’algorithme, la valeur contenue dans la variable u soit celle de u_5 . Quel algorithme doit-on choisir ?
a)
u=2
n=0
For k in range( 5) :
u=2*n-3
n=n+1
b)
u=2
n=0
For k in range( 5) :
u_{n+1}=2*u_n-3
n=n+1
c)
u=2
For k in range( 5) :
u=2*u-3
d)
u=4
n=0
While \leq 5 :
u=2*u-3
n=n+1
Exercice n°4
On considère la suite (u_n) définie par u_0=3 et par u_{n+1}=2u_n+2
Un algorithme permettant de calculer la somme S=u_0+u_1+…+u_{30} est :
a) U=3\\S=0Pour k de 1 à 29 S\leftarrow S+U | b) U=3\\S=0Pour k de 1 à 30 S\leftarrow S+U | c) U=3 S=3 Pour k de 1 à 30 S\leftarrow S+U | d) U=3 S=3 Pour k de 1 à 29 S\leftarrow S+U |
Exercice n°5
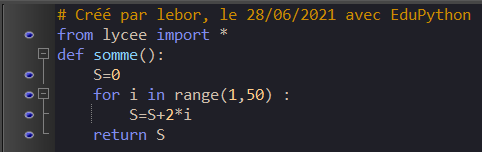
Voici un programme écrit en langage Python.
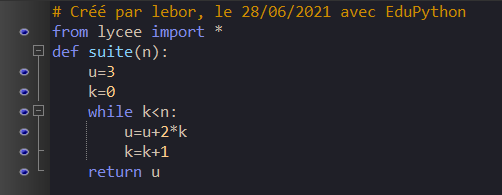
Quelle valeur obtient-on en tapant suite(4) dans la console Python ?
a)9 | b)15 | c)23 | d)33 |
Exercice n°6
On considère la suite (u_n) définie par u_0=5 et par u_{n+1}=4u_n-5
On veut déterminer la plus petite valeur de n telle que u_n soit supérieur ou égal à 10 000. On réalise pour cela le programme incomplet ci-dessous écrit en langage Python. Compléter les pointillés.
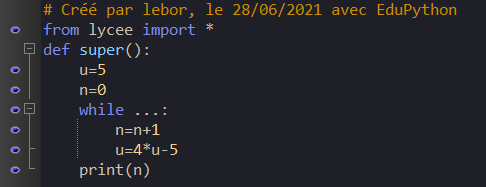
a)u\geq 10000 | b)u<10000 | c)n\geq 10000 | d)n<10000 |
Exercice n°7
Voici un programme écrit en langage Python.
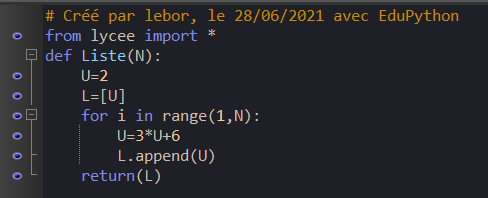
Si on tape Liste(4) dans la console, qu’obtient-on?
a)132 | b)42 | c)[2,12,42,132] | d)[2,12,42] |
Exercice n°8
On considère la suite (u_n) définie par u_0=200 et par u_{n+1}=0.7u_n-1
Quelle valeur renvoie ce programme écrit en langage Python ?
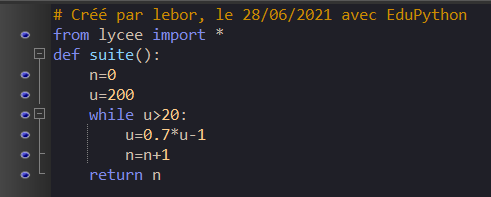
a) Le plus petit entier n tel que u_n>20. | b) Le plus petit entier n tel que u_n\leq 20. | c) Le premier terme de la suite tel que u_n>20. | d) Le premier terme de la suite tel que u_n\leq 20 |
Exercice n°9
Quel programme permet de calculer la somme des nombres entiers pairs de 2 à 100 ?
a)
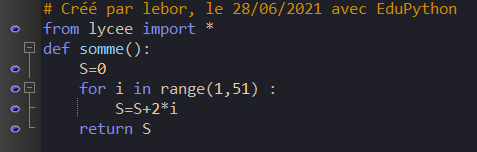
b)
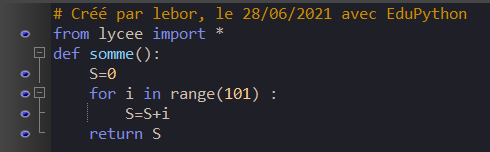
c)
d)