L’inéquation x^2-3x+2>0 a pour ensemble solution :
a) ]-\infty;1[ \cup ]2;+\infty[ | b) ]-2;-1[ | c) ]1;2[ | d) ]-\infty;-2[ \cup ]-1;+\infty[ |
Comment utiliser la TI 83 Premium CE
Tout ce qui est proposé est réalisable même si la calculatrice est en mode examen.
On programme la fonction f(x)=x^2-3x+2
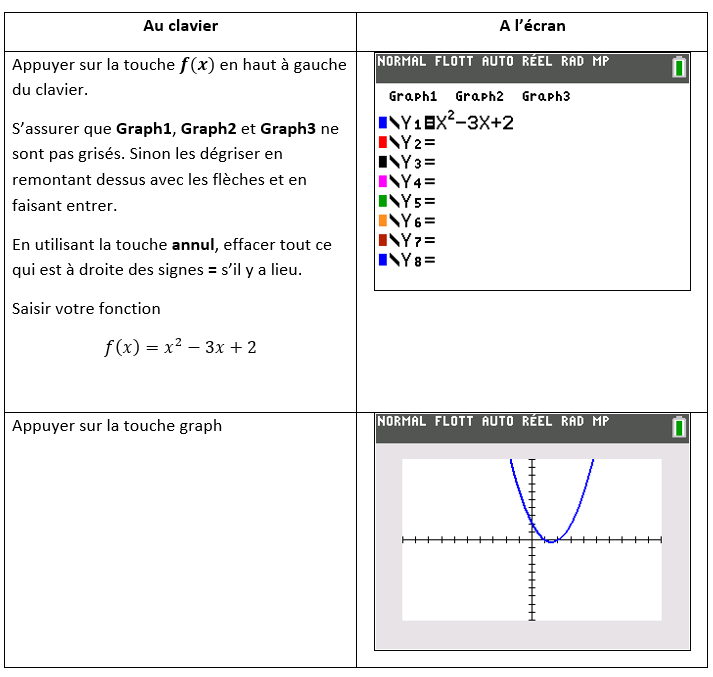
A l’aide du graphique, on voit que la courbe est toujours strictement au-dessus de l’axe des abscisses de -\infty à 1 puis de 2 à +\infty donc l’inéquation a pour solution l’ensemble ]-\infty;1[ \cup ]2;+\infty[



