Sommaire
Page Calcul Formel Géogébra pour conjecturer ou valider.
La page Calcul Formel de géogéba ci-dessous vous permettra de conjecturer ou de valider vos réponses. Attention toujours écrire les parenthèses pour saisir, par exemple l’équation ln(x)=1. Puis cliquer sur le septième onglet en partant de la gauche.
Exercice n°1
Résoudre les équations suivantes après avoir déterminé leur ensemble d’existence.
Remarque : la quantité écrite après ln doit toujours être strictement positive.
ln(2-4x)=2
ln(3x+9)=0
ln(x^2+2)=1
4+ln(x)=6
Exercice n°2
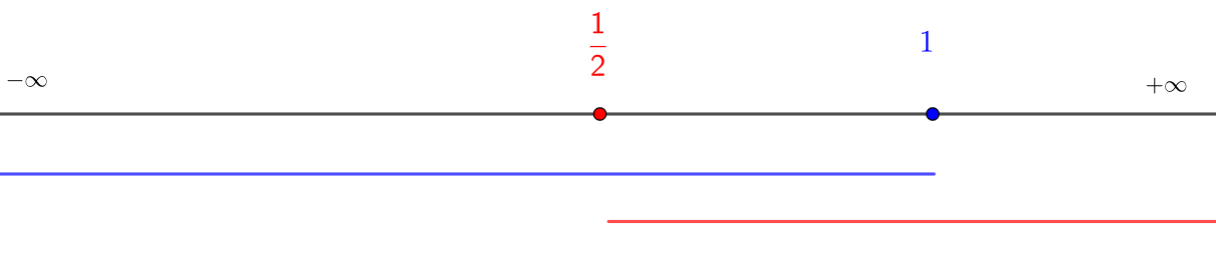
Résoudre les inéquations suivantes après avoir déterminé leur ensemble d’existence.
Remarque : la quantité écrite après ln doit toujours être strictement positive.
ln(3-x)>3
ln(2x-1)<0
ln(x^2)\leq 1
3+ln(x)\geq 2
Exercice n°3
Résoudre les équations suivantes après avoir déterminé leur ensemble d’existence.
Remarque : la quantité écrite après ln doit toujours être strictement positive.
ln(2-4x)=ln(4-2x)
ln(x)+ln(x-1)=ln(12)
2ln(x)=ln(4x-4)
Exercice n°4
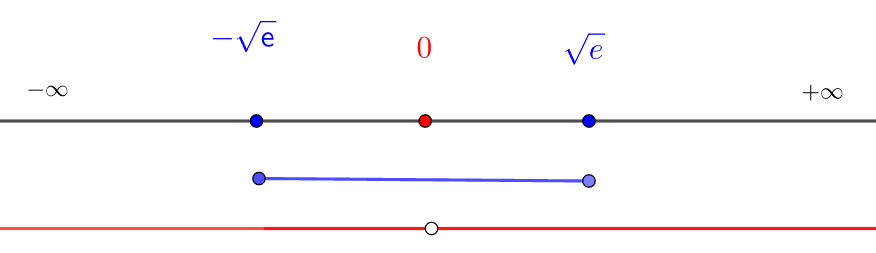
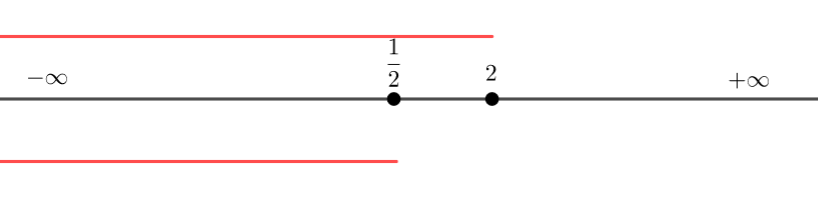
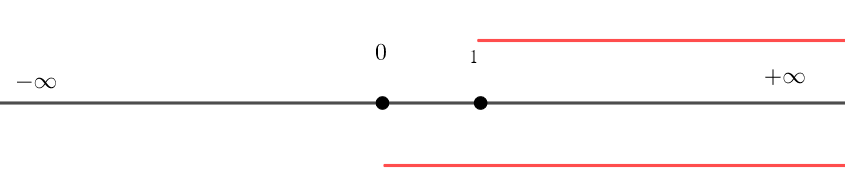
Résoudre les inéquations suivantes après avoir déterminé leur ensemble d’existence.
Remarque : la quantité écrite après ln doit toujours être strictement positive.
ln(2-2x)>ln(4+x)
ln(x)+ln(x-1)<ln(2)
2ln(x)\geq ln(6x-5)
Exercice n°5
Calculer les limites suivantes
\lim_{x\to 0}ln(x)+x^2
\lim_{x\to {+\infty}}xln(x)
\lim_{x\to {+\infty}}ln(x)-x
\lim_{x\to {0}}x^2ln(x)
\lim_{x\to 0}\frac{ln(x)-1}{x}
\lim_{x\to {+\infty}}\frac{ln(x)}{x^2}
\lim_{x\to {0}}(2x+1)ln(x)
\lim_{x\to {0}}6-ln(x)
Exercice n°6
Calculer f'(x) dans chaque cas.
f(x)=\frac{1}{x}+ln(x)
pour x \in ]0;+\infty[
f(x)=xln(x)
pour x \in ]0;+\infty[
f(x)=ln(x^2+5)
pour x \in \mathbf{R}
f(x)=(x-1)ln(2x)
pour x \in ]0;+\infty[
f(x)=\frac{ln(x)-1}{x}
pour x \in ]0;+\infty[
f(x)=ln^2(x)
pour x \in ]0;+\infty[
f(x)=\frac{ln(x)+1}{x^2}
pour x \in ]0;+\infty[
f(x)=ln(\frac{x-1}{x+1})
pour x \in ]1;+\infty[
Exercice n°7
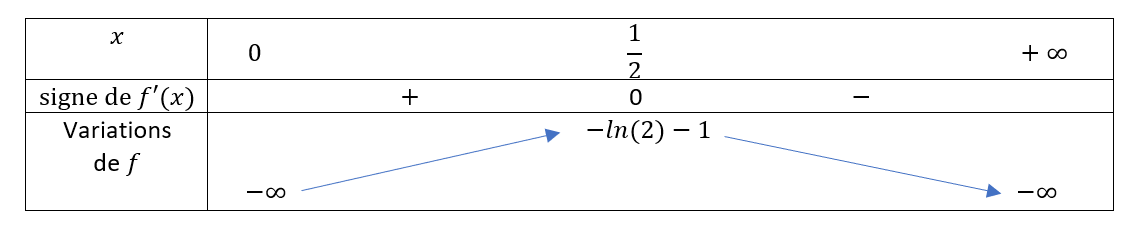
Soit la fonction f définie pour x \in ]0;+\infty[ par f(x)=ln(x)-2x
- Déterminer les limites de la fonction f aux bornes de son ensemble de définition.
C’est-à-dire en 0 et en +\infty.
2. a. Calculer f'(x)
2. b. Etudier le signe de f'(x) .
2. c. En déduire le tableau de variations de f sur ]0;+\infty[ .
3. Déterminer, par le calcul, l’équation de la tangente à la courbe de f au point d’abscisse 1 .
Exercice n°8
Soit la fonction f définie pour x \in ]0;+\infty[ par f(x)=ln(x^2)-2x+3
- Déterminer les limites de la fonction f aux bornes de son ensemble de définition.
C’est-à-dire en 0 et en +\infty.
2. a. Calculer f'(x)
2. b. Etudier le signe de f'(x) .
2. c. En déduire le tableau de variations de f sur ]0;+\infty[ .
3. Déterminer, par le calcul, l’équation de la tangente à la courbe de f au point d’abscisse 2 .
Exercice n°9
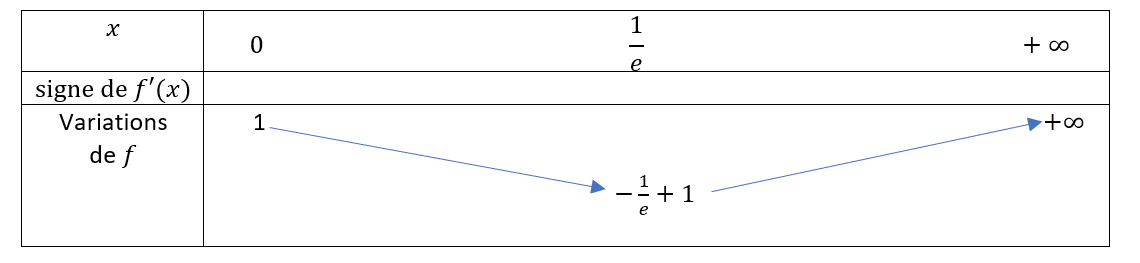
Soit la fonction f définie pour x \in ]0;+\infty[ par f(x)=xln(x)+1
- Déterminer les limites de la fonction f aux bornes de son ensemble de définition.
C’est-à-dire en 0 et en +\infty.
2. a. Calculer f'(x)
2. b. Etudier le signe de f'(x) .
2. c. En déduire le tableau de variations de f sur ]0;+\infty[ .
3. Déterminer, par le calcul, l’équation de la tangente à la courbe de f au point d’abscisse e .
Exercice n°10
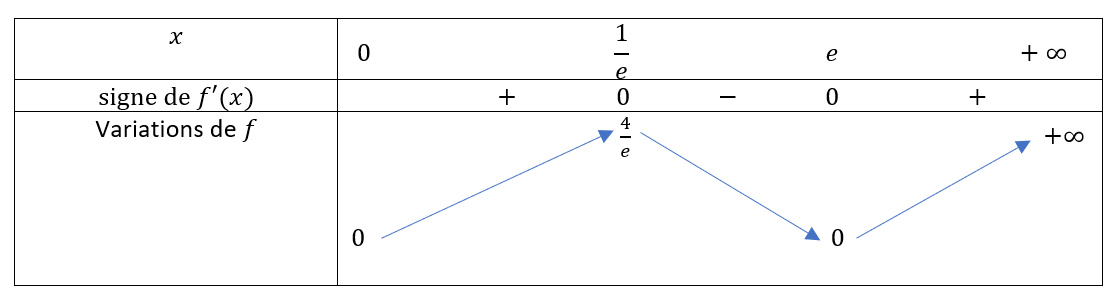
Soit la fonction f définie pour x \in ]0;+\infty[[ par f(x)=x(1-ln(x))^2
1. Calculer f'(x) et vérifier que f'(x)=(ln(x)+1)(ln(x)-1)
2. Etudier le signe de f'(x) .
3.a. Calculer f(e) et f(\frac{1}{e}) .
3. En déduire le tableau de variations de f sur ]0;+\infty[ . On admettra que \lim_{x\to 0}f(x)=0 et que \lim_{x\to +\infty}f(x)=+\infty