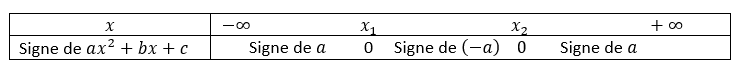logo

TC. Problème n°3 ( fonction convexe )

Exercice n°3

On considère la fonction f définie et dérivable sur \mathbf{R} par f(x)=(-5x^2+5)e^x 
Cette fonction admet sur R une dérivée f’ et une dérivée seconde f".
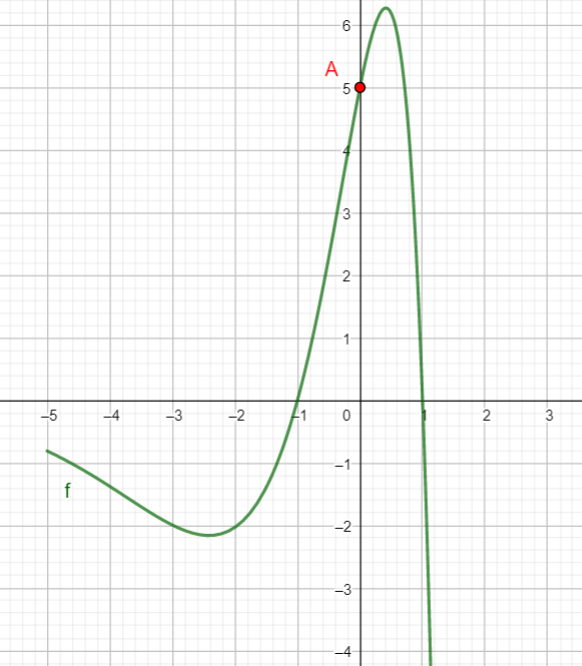
On donne ci-contre la courbe C_f représentative de la fonction f.

1. a. Calculer les coordonnées du point A , intersection de la courbe C_f avec l’axe des ordonnées. Placer le point A dans le repère ci-dessus.

correction

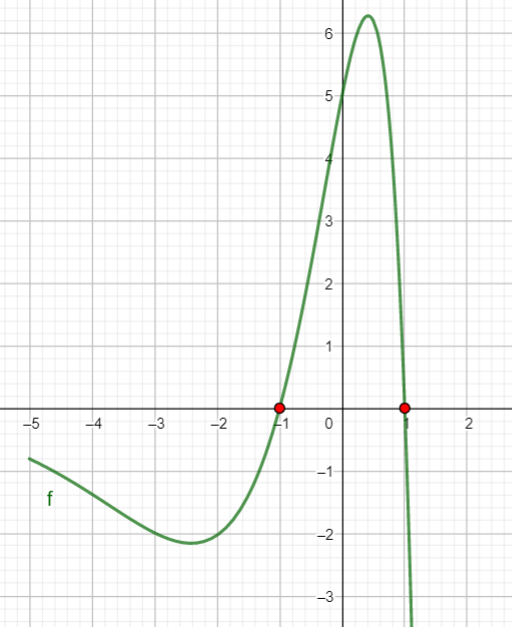
b. Déterminer par le calcul les coordonnées des points d’intersection de C_f et de l’axe des abscisses. Puis les placer dans le repère ci-dessus.

correction

c. Montrer que pour tout x ∈ R, f'(x)=(-5x^2-10x+5)e^x

correction

d. Étudier les variations de la fonction f sur l’intervalle [-5;2].

correction

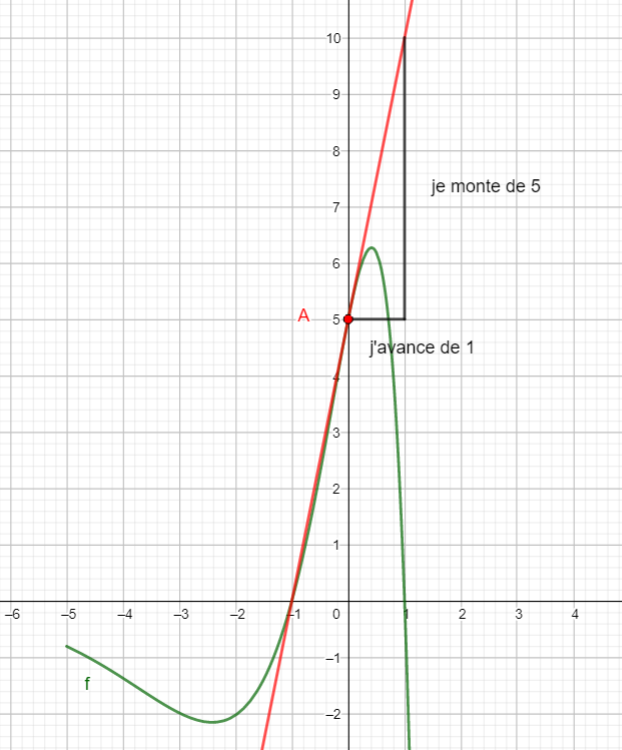
2. Soit \Delta la tangente à C_f au point d’abscisse 0.
a. Montrer qu’une équation de \Delta est y=5x+5

correction

b. Tracer la droite \Delta dans le repère ci-dessus.

correction

3. a Montrer que f"(x)=(-5x^2-20x-5)e^x.

correction

b. Étudier la convexité de la fonction f sur l’intervalle [-5;2]

correction

©2020 – Math’O karé SAS

 Calculer les coordonnées du point A , intersection de la courbe C_f avec l’axe des ordonnées.

On pose A(x_A;y_A).

A est sur la courbe C_f donc ses coordonnées (x_A;y_A) vérifient y_A=(-5x_A^2+5)e^{x_A}.

A est l’axe des ordonnées donc  x_A=0. 

y_A=(-5\times 0^2+5)e^{0}

y_A=5\times 1

y_A=5

Donc A(0;5).

Déterminer par le calcul les coordonnées des points d’intersection de C_f et de l’axe des abscisses. 

Il faut d’abord résoudre f(x)=0 pour déterminer les abscisses des points d’intersection.

(-5x^2+5)e^x=0

-5x^2+5=0 ( car e^x ne s’annule jamais)

On met -5 en facteur.

-5(x^2-1)=0

On factorise x^2-1 en utilisant une identité remarquable.

-5(x-1)(x+1)=0

On applique la règle du produit nul.

x-1=0 ou x+1=0

x=1 ou x=-1

Comme les points sont sur l’axe des abscisses, leur ordonnée est nulle.

Les deux points d’intersection ont pour coordonnées : (-1;0) et (1;0).

f(x)=(-5x^2+5)e^x

1.On veut calculer f'(x).

On répond à la question suivante : est-ce une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est le produit de deux fonctions u\times v avec  u(x)=-5x^2+5 et v(x)=e^x.

On va utiliser la ligne n°3 du tableau n°1 ci-dessous.

Dérivées et opérations

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

2a.on veut calculer la dérivée  u'(x)

u(x)=-5x^2+5 est une somme

u'(x)=(-5x^2+5)’

u'(x)=(-5x^2)’+(5)’

u'(x)=-5\times(x^2)’+0

u'(x)=-5\times 2x

u'(x)=-10x

2b.on veut calculer la dérivée  v'(x)

v(x)=e^{x}

C’est une fonction de référence.

v'(x)=(e^{x})’

v'(x)=e^{x}

3. On calcule la dérivée f'(x) 

On remplace u par  -5x^2+5,  v par e^{x}, u’ par  -10x et v’ par e^x dans la formule u’\times v+u\times v’ 

f'(x)=(-5x^2+5)’e^{x}+(-5x^2+5)(e^{x})’\\f'(x)=-10x\times e^{x}+(-5x^2+5)\times e^{x}\\f'(x)= -10xe^{x}+(-5x^2+5)e^{x}

On met e^{x} en facteur.

f'(x)= e^{x}(-10x-5x^2+5)\\f'(x)= e^{x}(-5x^2-10x+5)

 

 

On veut étudier le signe de f'(x)=(-5x^2-10x+5)e^x.

Comme e^x est toujours positif, f'(x) est du signe de -5x^2-10x+5.

On étudie donc le signe de -5x^2-10x+5.

On utilise la troisième ligne du tableau ci-dessous : la quantité est de la forme ax^2+bx+c.

  1. de nombres positifs alors la quantité est positive.
  2. de nombres négatifs alors la quantité est négative.
  3. de nombres de signes contraires ou indéterminés alors on ne peut pas conclure

On peut factoriser et étudier le signe d’un produit

On peut résoudre la quantité >0 

…

On utilise le tableau suivant :

On utilise le résultat du cours suivant :

si \Delta>0

si \Delta=0

si \Delta<0

La quantité est toujours positive.

Exemples : les quantités x^2 , (2x+5)^4 sont toujours positives

La quantité est du signe de ce qui est élevé à la puissance.

Exemple : la quantité x^3 est du signe de x, la quantité (2x-1)^5 est du signe de 2x-1.

On fait un tableau de signes comme en seconde : on étudie le signe de chaque facteur et on applique la règle des signes.

On fait un tableau de signes comme en seconde : on étudie le signe du numérateur, le signe du dénominateur et on applique la règle des signes.

On calcule la dérivée, on étudie son signe et on fait le tableau de variations. Ensuite, sur la dernière ligne du tableau de variations, on lit le signe de la quantité.  

J’identifie les coefficients du polynôme. a=-5, b=-10 et c=5.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par (-5),(-10) ,5  .

\Delta=(-10)²-4\times{(-5)}\times{5}\\\Delta=100+100\\\Delta=200

Comme \Delta>0 , l’équation admet deux solutions réelles notées

x_1=\frac{-b-\sqrt{\Delta}}{2a} et x_2=\frac{-b+\sqrt{\Delta}}{2a}.

ax²+bx+c est  du signe de a à l’extérieur des racines et du signe de (-a) à l’intérieur des racines.

Je calcule x_1=\frac{-b-\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par (-5), (-10), 200.

x_1=\frac{-(-10)-\sqrt{200}}{2\times{(-5)}}\\x_1=\frac{10-10\sqrt{2}}{-10}\\x_1=-\frac{10-10\sqrt{2}}{10}\\x_1=-(1-\sqrt{2})\\x_1=-1+\sqrt{2}

Je calcule x_2=\frac{-b+\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par (-5), (-10), 200

x_2=\frac{-(-10)+\sqrt{200}}{2\times{(-5)}}\\x_2=\frac{10+10\sqrt{2}}{-10}\\x_2=-\frac{10+10\sqrt{2}}{10}\\x_2=-(1+\sqrt{2})\\x_2=-1-\sqrt{2}

Je dresse le tableau de signes du polynôme:

Comme a=-5 le signe de a est négatif.

Sur l’intervalle [-5;-1-\sqrt{2}]\cup [-1+\sqrt{2};2] , f'(x) est négative donc  f est décroissante.

Sur l’intervalle [-1-\sqrt{2};-1+\sqrt{2}] , f'(x) est positive donc  f est croissante.

 

 

On veut déterminer l’équation de  \Delta la tangente à C_f au point d’abscisse 0.
1.on calcule f(0) en remplaçant tous les x par 0 dans f(x)=(-5x^2+5)e^x.

f(0)=(-5\times 0^2+5)e^0

f(0)=(0+5)\times 1

f(0)=5

2.on calcule f'(0) en remplaçant tous les x par 0 dans f(x)=(-5x^2-10x+5)e^x.

f'(0)=(-5\times 0^2-10\times 0+5)e^0

f'(0)=(0+5)\times 1

f'(0)=5

3.on détermine l’équation de  \Delta en remplaçant  a par 0, f(a) par 5 et f'(a) par 5 dans

y=f'(a)(x-a)+f(a).

y=5(x-0)+5

y=5x+5

 

L’équation de la tangente est y=5x+5.

L’ordonnée à l’origine vaut 5. On fait une croix sur l’axe des ordonnées à la graduation 5.

Le coefficient directeur vaut 5 aussi. A partir du point précédent, j’avance de une graduation vers la droite et je monte verticalement de 5 graduations. Je fais alors une deuxième croix. Je trace ensuite la droite qui passe par les deux croix.

f'(x)= (-5x^2-10x+5)e^{x}.

1.On veut calculer f"(x).

On répond à la question suivante : est-ce une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est le produit de deux fonctions u\times v avec  u(x)=-5x^2-10x+5 et v(x)=e^x.

On va utiliser la ligne n°3 du tableau n°1 ci-dessous.

Dérivées et opérations

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

2a.on veut calculer la dérivée  u'(x)

u(x)=-5x^2-10x+5 est une somme

u'(x)=(-5x^2-10x+5)’

u'(x)=(-5x^2)’-(10x)’+(5)’

u'(x)=-5\times(x^2)’-10(x)’+0

u'(x)=-5\times 2x-10\times 1

u'(x)=-10x-10

2b.on veut calculer la dérivée  v'(x)

v(x)=e^{x}

C’est une fonction de référence.

v'(x)=(e^{x})’

v'(x)=e^{x}

3. On calcule la dérivée f"(x) 

On remplace u par  -5x^2-10x+5,  v par e^{x}, u’ par  -10x-10 et v’ par e^x dans la formule u’\times v+u\times v’ 

f"(x)=(-5x^2-10x+5)’e^{x}+(-5x^2-10x+5)(e^{x})’\\f"(x)=(-10x-10)\times e^{x}+(-5x^2-10x+5)\times e^{x}

On met e^{x} en facteur.

f"(x)= e^{x}(-10x-10-5x^2-10x+5)\\f"(x)= e^{x}(-5x^2-20x-5)

On veut étudier le signe de f"(x)=(-5x^2-20x-5)e^x.

Comme e^x est toujours positif, f"(x) est du signe de -5x^2-20x-5.

On étudie donc le signe de -5x^2-20x-5.

On utilise la troisième ligne du tableau ci-dessous : la quantité est de la forme ax^2+bx+c.

  1. de nombres positifs alors la quantité est positive.
  2. de nombres négatifs alors la quantité est négative.
  3. de nombres de signes contraires ou indéterminés alors on ne peut pas conclure

On peut factoriser et étudier le signe d’un produit

On peut résoudre la quantité >0 

…

On utilise le tableau suivant :

On utilise le résultat du cours suivant :

si \Delta>0

si \Delta=0

si \Delta<0

La quantité est toujours positive.

Exemples : les quantités x^2 , (2x+5)^4 sont toujours positives

La quantité est du signe de ce qui est élevé à la puissance.

Exemple : la quantité x^3 est du signe de x, la quantité (2x-1)^5 est du signe de 2x-1.

On fait un tableau de signes comme en seconde : on étudie le signe de chaque facteur et on applique la règle des signes.

On fait un tableau de signes comme en seconde : on étudie le signe du numérateur, le signe du dénominateur et on applique la règle des signes.

On calcule la dérivée, on étudie son signe et on fait le tableau de variations. Ensuite, sur la dernière ligne du tableau de variations, on lit le signe de la quantité.  

J’identifie les coefficients du polynôme. a=-5, b=-20 et c=-5.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par (-5),(-20) ,(-5)  .

\Delta=(-20)²-4\times{(-5)}\times{(-5)}\\\Delta=400-100\\\Delta=300

Comme \Delta>0 , l’équation admet deux solutions réelles notées

x_1=\frac{-b-\sqrt{\Delta}}{2a} et x_2=\frac{-b+\sqrt{\Delta}}{2a}.

ax²+bx+c est  du signe de a à l’extérieur des racines et du signe de (-a) à l’intérieur des racines.

Je calcule x_1=\frac{-b-\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par (-5), (-20), 300.

x_1=\frac{-(-20)-\sqrt{300}}{2\times{(-5)}}\\x_1=\frac{20-10\sqrt{3}}{-10}\\x_1=-\frac{20-10\sqrt{3}}{10}\\x_1=-(2-\sqrt{3})\\x_1=-2+\sqrt{3}

Je calcule x_2=\frac{-b+\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par (-5), (-20), 300

x_2=\frac{-(-20)+\sqrt{300}}{2\times{(-5)}}\\x_2=\frac{20+10\sqrt{3}}{-10}\\x_2=-\frac{20+10\sqrt{3}}{10}\\x_2=-(2+\sqrt{3})\\x_2=-2-\sqrt{3}

Je dresse le tableau de signes du polynôme:

Comme a=-5 le signe de a est négatif.

Sur l’intervalle [-5;-2-\sqrt{3}]\cup [-2+\sqrt{3};2] , f"(x) est négative donc  f est concave.

Sur l’intervalle [-2-\sqrt{3};-2+\sqrt{3}] , f"(x) est positive donc  f est convexe.

 

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.