Définition
Dans une succession d’épreuves, lorsque l’issue d’une épreuve ne dépend pas des épreuves précédentes, on dit que ces épreuves sont indépendantes.
Situation n°1 : épreuves indépendantes
Une urne contient 1 boule rouge et 4 boules vertes. On tire une boule de l’urne on note sa couleur et on la remet dans l’urne. On effectue ainsi 2 tirages.
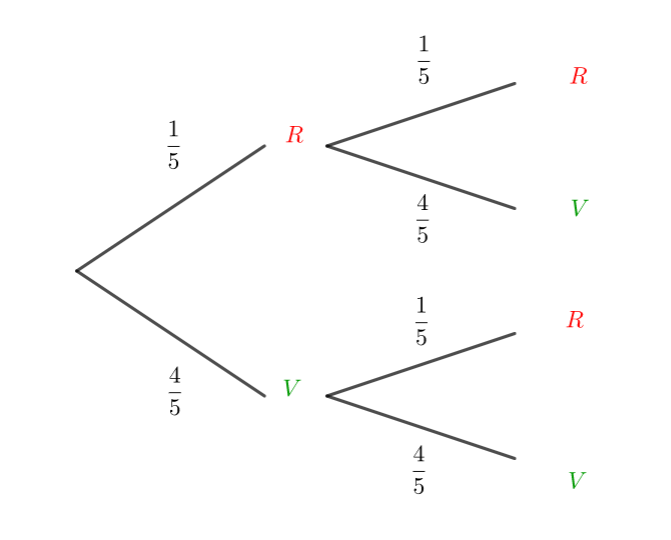
Qu’on tire une boule verte ou rouge au premier tirage, la probabilité de tirer une boule rouge au second tirage, par exemple, sera toujours \frac{1}{5} au deuxième tirage.
Le résultat du second tirage ne dépend pas du résultat du premier tirage.
Il s’agit là d’une succession de 2 épreuves indépendantes.
Situation n°2 : épreuves non indépendantes
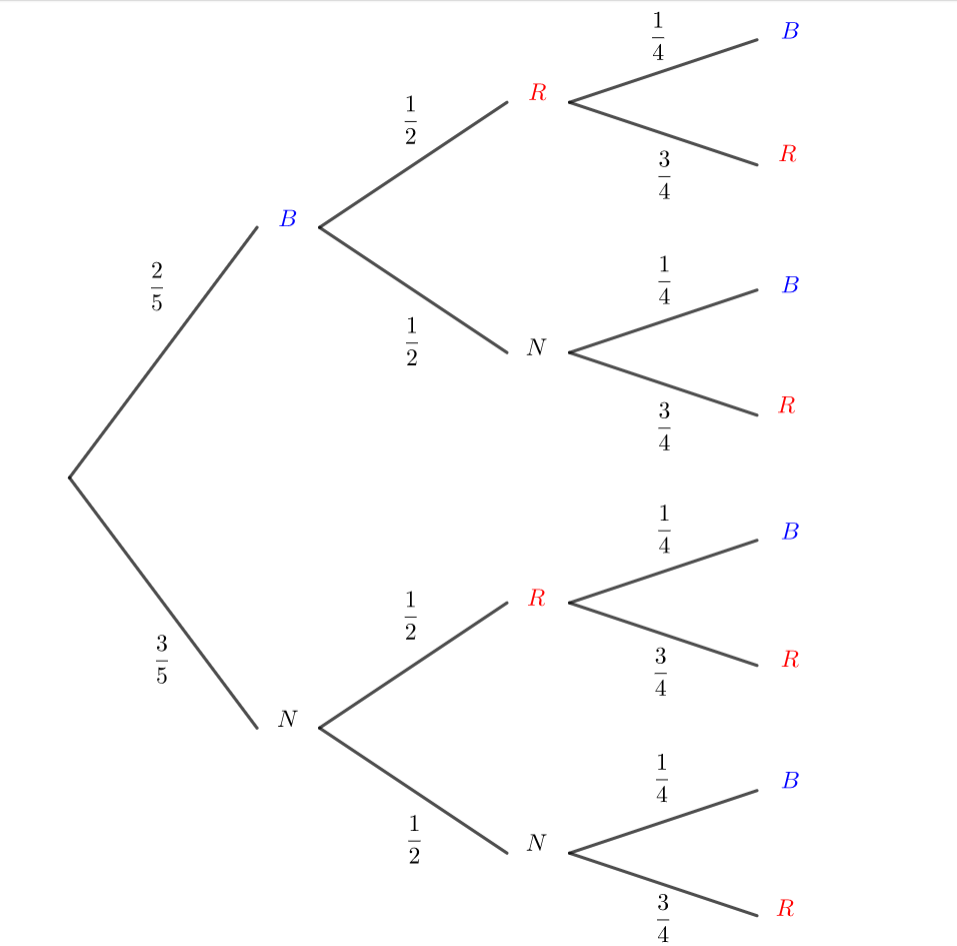
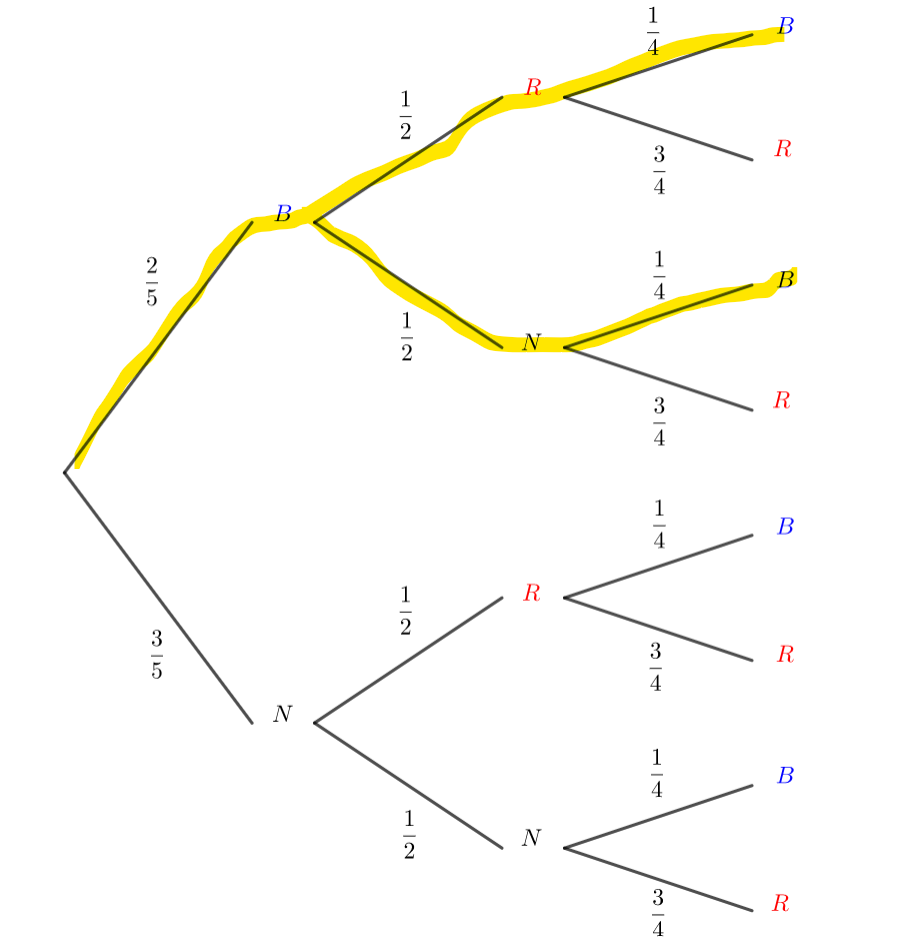
Une urne contient 1 boule rouge et 4 boules vertes. On tire une boule de l’urne on note sa couleur et on ne la remet pas dans l’urne. On effectue ainsi 2 tirages.
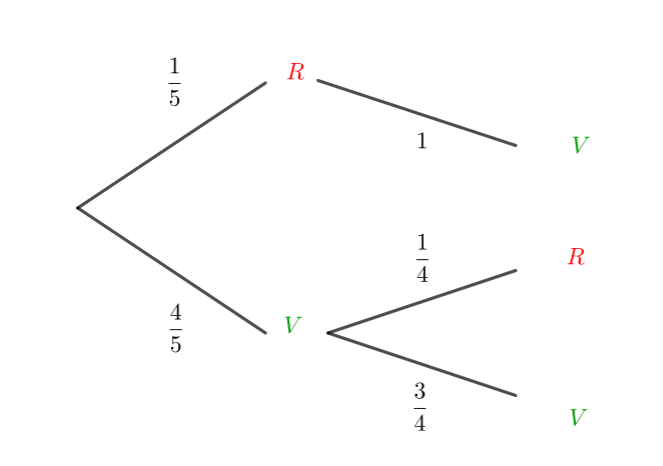
Si on a tiré une boule rouge au premier tirage, la probabilité de tirer une boule verte au second tirage est 1.
Si on a tiré une boule verte au premier tirage, la probabilité de tirer une boule verte au second tirage est \frac{3}{4}.
On voit donc que suivant le résultat du second tirage dépend du résultat du premier tirage.
Il s’agit là d’une succession de 2 épreuves qui ne sont pas indépendantes.
Propriété
Dans une succession de n épreuves, la probabilité d’une issue x_1;x_2;…;x_n est égale au produit des probabilités de x_1 , x_2;… ….et x_n.
Exemple
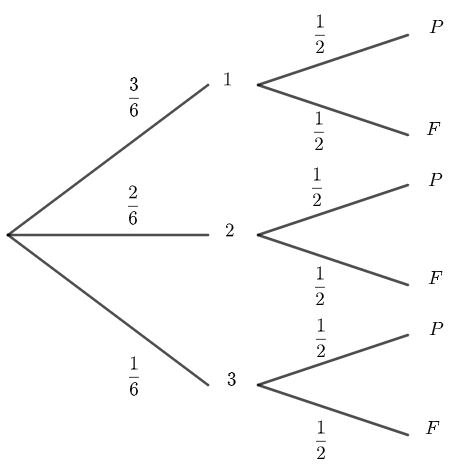
On tire au hasard une boule dans une urne qui contient trois boules numérotées 1, 2 et 3. Puis on lance une pièce de monnaie.
On modélise l’univers de cette expérience avec l’arbre suivant :
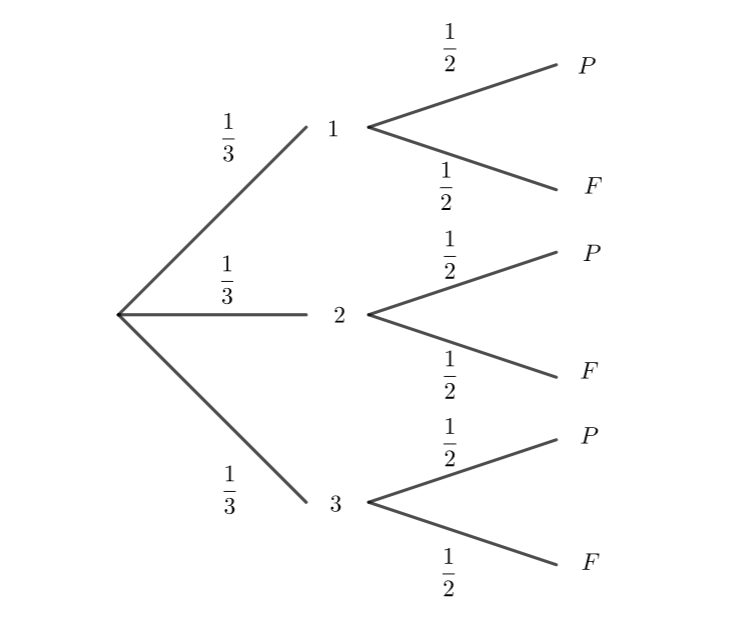
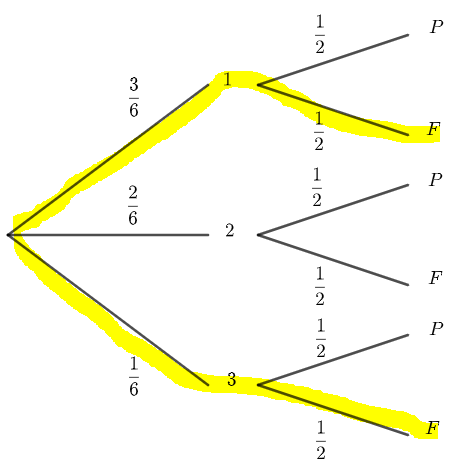
Il s’agit de la succession de deux épreuves indépendantes, donc pour calculer par exemple p(1;F), on calcule \frac{1}{3}\times\frac{1}{2}.
p(1;F)=\frac{1}{6}.
On procède de la même façon pour les autres issues.
Exercice n°1
On tire successivement une boule dans chacune des trois urnes.
Dans l’urne n°1, se trouvent 2 boules blanches et 3 boules noires.
Dans l’urne n°2, se trouve 1 boule rouge et 1 boule noire.
Dans l’urne n°3, se trouve 1 boule blanche et 3 boules rouges.
1. modéliser l’univers de cette expérience à l’aide d’un arbre.
2. Déterminer la probabilité de l’évènement » la première boule tirée et la dernière boule tirée sont de la même couleur ».
Exercice n°2
Un dé équilibré à 6 faces a trois faces qui portent le numéro 1 , 2 faces qui portent le numéro 2 et une face qui porte le numéro 3
On jette le dé et ensuite on jette une pièce équilibrée.
1. modéliser l’univers de cette expérience à l’aide d’un arbre.
2. Déterminer la probabilité de l’évènement » la boule tirée porte un numéro impair et on a obtenu face avec la pièce « .
Exercice n°3
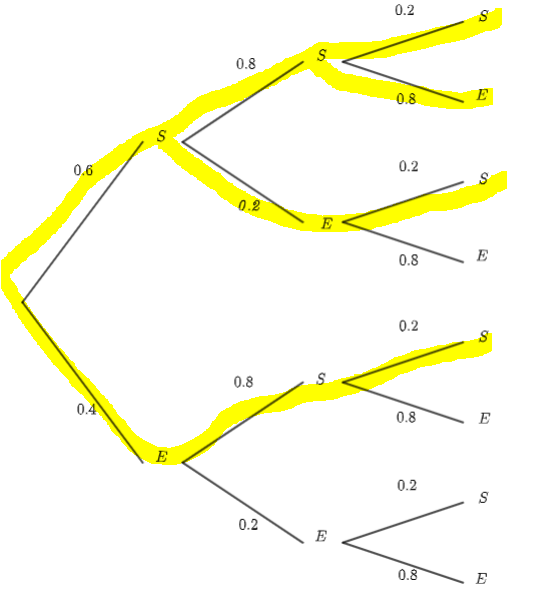
Un examen est composé de trois épreuves indépendantes.
En général, l’épreuve 1 est réussie a 60 %, l’épreuve 2 à 80% et l’épreuve 3 à 20% .
Pour être reçu à l’examen, il faut réussir au moins deux épreuves.
Quelle est la probabilité d’être reçu à l’examen ?