Sommaire
Exercice n°1
X suit une loi binomiale de paramètres n=20 et p=0.7
A l’aide de la calculatrice, calculer :
Exercice n°2
X suit une loi binomiale de paramètres n=15 et p=0.2
A l’aide de la calculatrice, calculer :
Exercice n°3
Une entreprise produit en grande quantité des stylos. La probabilité qu’un stylo présente un défaut est
égale à 0.1.
On prélève dans cette production, successivement et avec remise huit stylos.
On note X la variable aléatoire qui compte le nombre de stylos présentant un défaut parmi
les huit stylos prélevés.
a) On admet que X suit une loi binomiale. Donner les paramètres de cette loi.
b) Calculer la probabilité des événements suivants :
A : « il n’y a aucun stylo avec un défaut » ;
B : « il y a au moins un stylo avec un défaut » ;
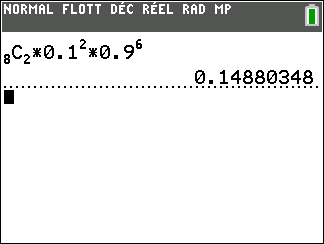
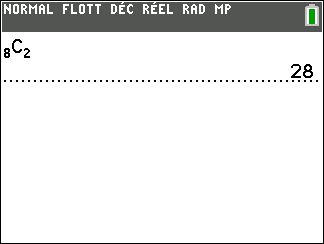
C : « il y a exactement deux stylos avec un défaut ».
Exercice n°4
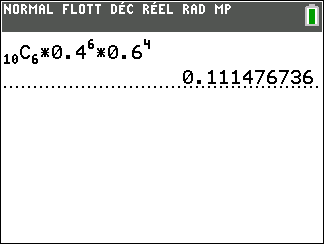
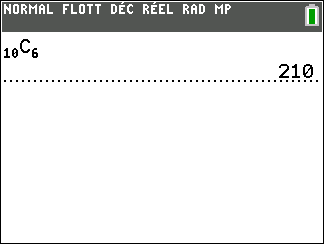
Dans une urne il y a 6 boules noires et 4 boules rouges. On effectue successivement 10 tirages aléatoires avec remise. Quelle est la probabilité (à 10^{-4} près) d’avoir
4 boules noires et 6 boules rouges ?
Parmi les quatre réponses, quelle est la bonne réponse ?
a. 0.1662
b. 0.4
c. 0.1115
d. 0.8886
Exercice n°5
Dans un centre de traitement du courrier, une machine est équipée d’un lecteur optique automatique de reconnaissance de l’adresse postale. Ce système de lecture permet de reconnaître convenablement 97 % des adresses; le reste du courrier, que l’on qualifiera d’illisible pour la machine, est orienté vers un employé du centre chargé de lire les adresses.
Cette machine vient d’effectuer la lecture de neuf adresses. On note X la variable aléatoire qui donne le nombre d’adresses illisibles parmi ces neuf adresses.
On admet que X suit la loi binomiale de paramètres n=9 et p=0.03.
1. La probabilité qu’aucune des neuf adresses soit illisible est égale, au centième près, à :
a. 0
b. 1
c. 0.24
d. 0.76
2. La probabilité qu’exactement deux des neuf adresses soient illisibles pour la machine est :
a. \binom{9}{2}\times 0.97^2\times 0.03^7
b. \binom{7}{2}\times 0.97^2\times 0.03^7
c. \binom{9}{2}\times 0.97^7\times 0.03^2
d. \binom{7}{2}\times 0.97^7\times 0.03^2
3. La probabilité qu’au moins une des neuf adresses soit illisible pour la machine est :
a. p(X<1)
b. p(X\leq 1)
c. p(X\geq 2)
d. 1-p(X=0)
Exercice n°6
On choisit dans le centre vétérinaire un échantillon de 20 chats au hasard. On admet que l’on peut assimiler ce choix à un tirage avec remise.
La probabilité que le test du chat soit positif est égale à 0.45.
On note X la variable aléatoire donnant le nombre de chats présentant un test positif dans l’échantillon choisi.
a. Déterminer, en justifiant, la loi suivie par la variable aléatoire X
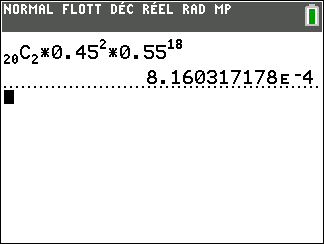
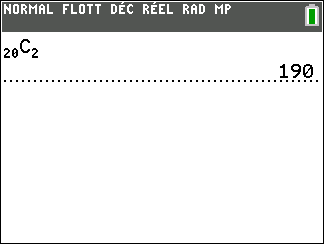
b. Calculer la probabilité qu’il y ait dans l’échantillon exactement 2 chats présentant un test positif.
c. Calculer la probabilité qu’il y ait dans l’échantillon au plus 8 chats présentant un test positif.
d. Calculer la probabilité qu’il y ait dans l’échantillon entre 5 et 9 chats présentant un test positif ( les valeurs 5 et 9 sont incluses).
e. Déterminer l’espérance de la variable aléatoire X et interpréter le résultat dans le contexte
de l’exercice.
Exercice n°7
Un restaurant propose deux types de plats à emporter : le plat du jour et des pizzas.
Le restaurant propose également plusieurs desserts.
Le propriétaire constate que 60% des clients choisissent le plat du jour et que parmi ceux-ci 80% prennent également un dessert.
Elle constate aussi que 75 % des clients qui ont choisi une pizza ne prennent pas de dessert.
On choisit au hasard un client .
On considère les évènements suivants :
J : « Le client interrogé a choisi le plat du jour ».
D : « Le client interrogé a choisi un dessert ».
Partie A
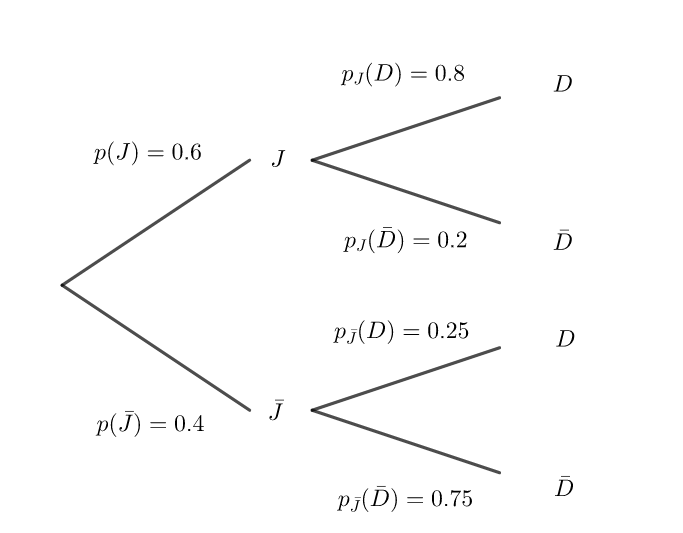
1. Recopier puis compléter l’arbre pondéré suivant :
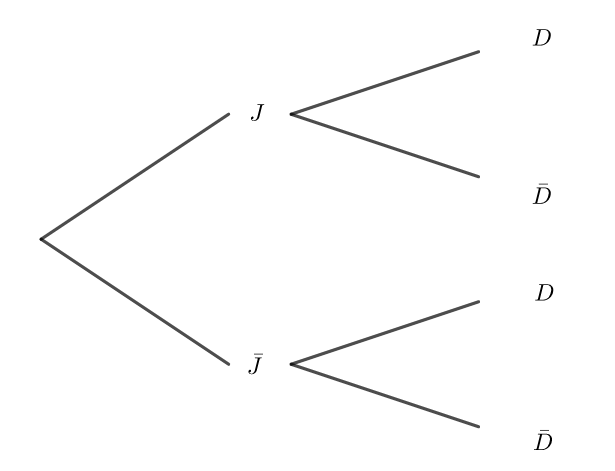
2. Calculer la probabilité que le client ait choisi un plat du jour et un dessert.
3. Démontrer que p(D)=0.58 .
4. Sachant que le client a acheté un dessert, quelle est la probabilité, arrondie à 0, 01 près, qu’il
ait acheté une pizza ?
5. Les événements J et D sont-ils indépendants ?
Partie B
On a montré dans la partie A que p(D)=0.58.
On choisit dans ce restaurant un échantillon de 30 clients au hasard. On admet que l’on peut assimiler ce choix à un tirage avec remise.
On note X la variable aléatoire donnant le nombre de clients ayant pris un dessert dans l’échantillon choisi.
1. Déterminer, en justifiant, la loi suivie par la variable aléatoire X
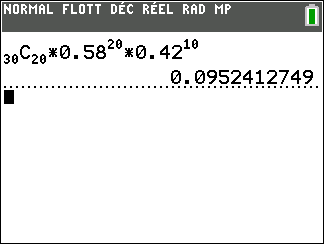
2. Calculer la probabilité qu’il y ait dans l’échantillon exactement 20 personnes qui aient choisi un dessert.
3. Déterminer l’espérance de la variable aléatoire X et interpréter le résultat dans le contexte de l’exercice.
Exercice n°8
Pendant la semaine du blanc, une grande surface a mis en vente un lit à 499 euros et une parure de draps à 49 euros.
On a constaté que 40% des clients du magasin ont acheté un lit .
Parmi les clients ayant acheté un lit, 70 % ont acheté une parure de draps
Parmi les clients du magasin n’ayant pas acheté de lit, 25 % ont tout de même acheté une parure de draps.
On choisit au hasard un client. On admet qu’un client achète au plus un lit et au plus une parure de draps.
On note les événements suivants :
L « le client achète un lit »
D « le client achète une parure de draps ».
Partie 1
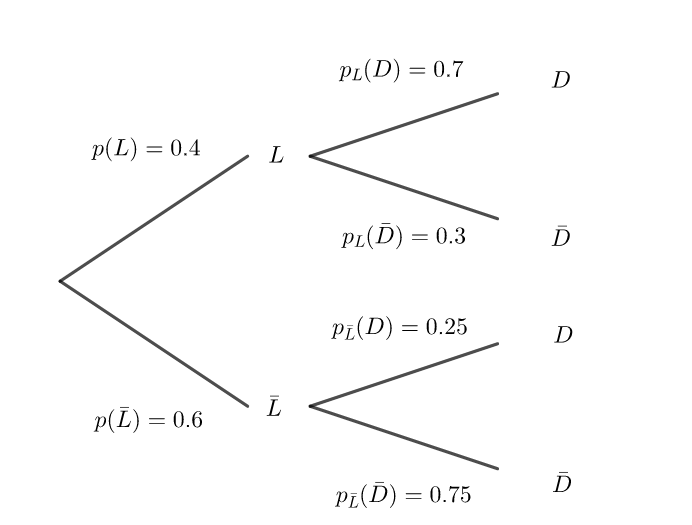
1. Reproduire sur la copie et compléter l’arbre pondéré ci-dessous décrivant la situation.
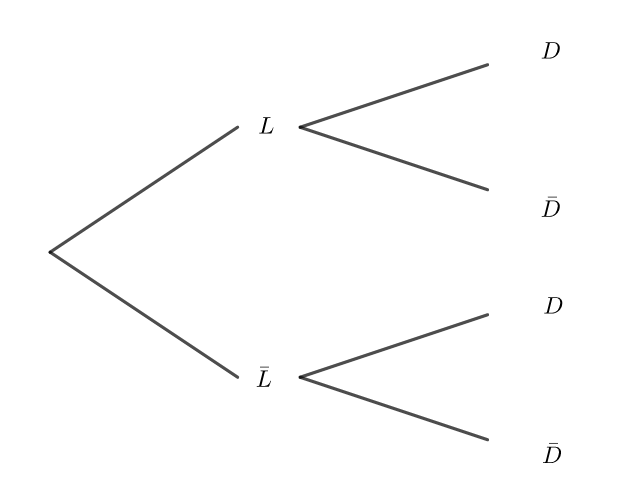
2. Calculer la probabilité que le client achète un lit et une parure de draps.
3. Montrer que la probabilité de l’événement D est égale à 0.43.
4. Calculer la probabilité que le client achète un lit sachant qu’il a acheté une parure de draps.
5. On appelle S la variable aléatoire donnant la somme dépensée par un client au rayon literie.
Calculer l’espérance mathématique de 𝐷 et donner une interprétation de ce nombre dans le contexte de l’exercice.
Partie B
La probabilité de l’événement D est égale à 0.43.
On choisit dans ce magasin un échantillon de 100 clients au hasard. On admet que l’on peut assimiler ce choix à un tirage avec remise.
On note X la variable aléatoire donnant le nombre de clients ayant acheté une parure de draps.
1. Déterminer, en justifiant, la loi suivie par la variable aléatoire X
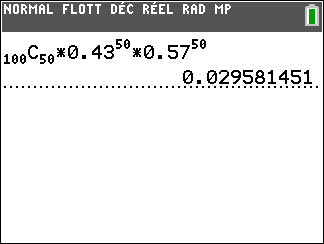
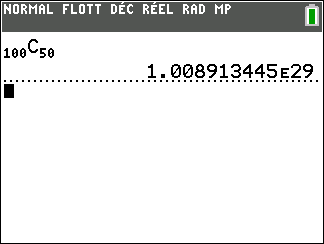
2. Calculer la probabilité qu’il y ait dans l’échantillon exactement 50 personnes qui aient acheté une parure de draps.
3. Déterminer l’espérance de la variable aléatoire X et interpréter le résultat dans le contexte de l’exercice.