Sommaire
Exercice n°1
Pour préparer l’examen du permis de conduire, on distingue deux types de formation :
— la formation avec conduite accompagnée ;
— la formation traditionnelle.
On considère un groupe de 300 personnes venant de réussir l’examen du permis de conduire.
Dans ce groupe :
— 75 personnes ont suivi une formation avec conduite accompagnée ; parmi elles, 50 ont réussi
l’examen à leur première présentation et les autres ont réussi à leur deuxième présentation.
— 225 personnes se sont présentées à l’examen suite à une formation traditionnelle ; parmi
elles, 100 ont réussi l’examen à la première présentation, 75 à la deuxième et 50 à la troisième présentation.
On interroge au hasard une personne du groupe considéré.
On considère les évènements suivants :
A : « la personne a suivi une formation avec conduite accompagnée »;
R_1 : « la personne a réussi l’examen à la première présentation » ;
R_2: « la personne a réussi l’examen à la deuxième présentation » ;
R_3 : « la personne a réussi l’examen à la troisième présentation ».
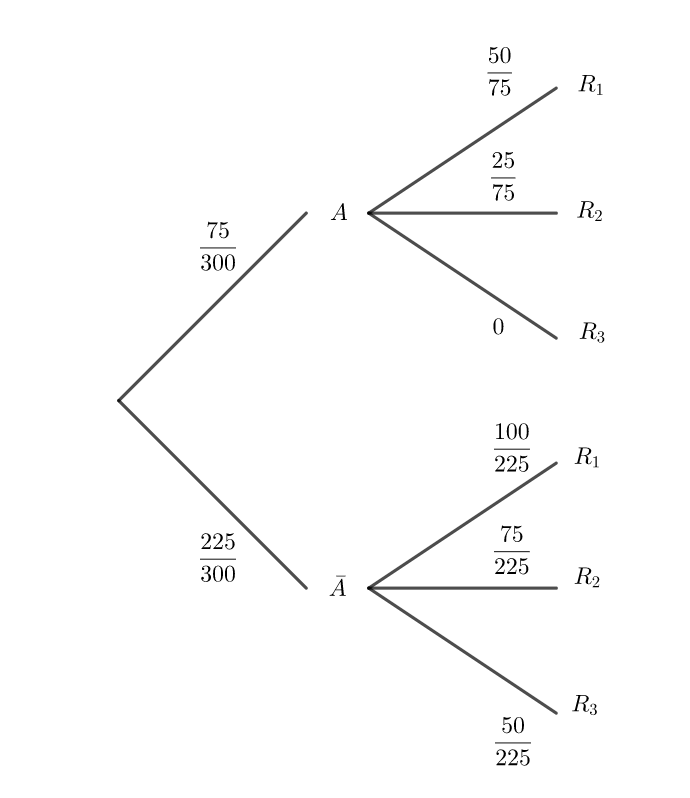
1. Modéliser la situation par un arbre pondéré.
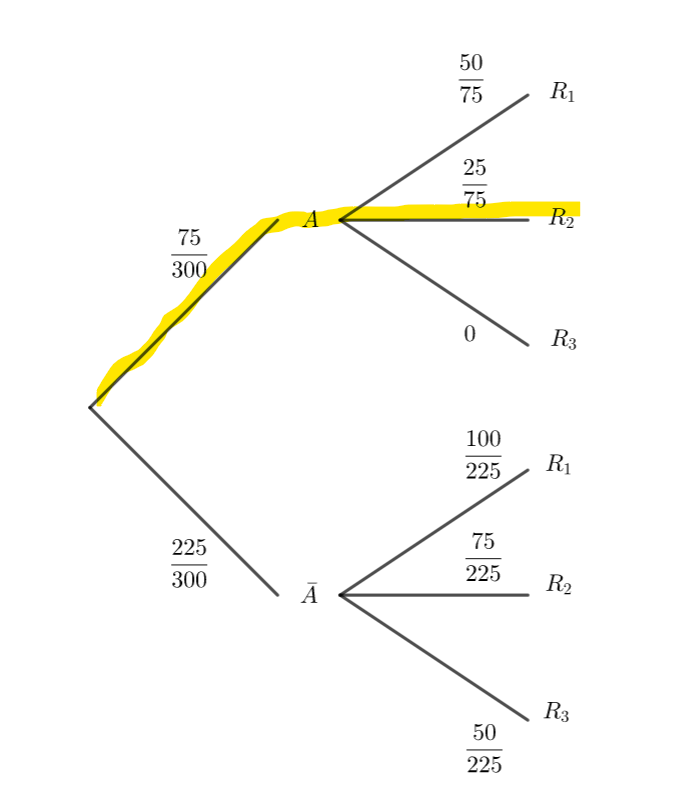
2. a. Calculer la probabilité que la personne interrogée ait suivi une formation avec conduite accompagnée et réussi l’examen à sa deuxième présentation
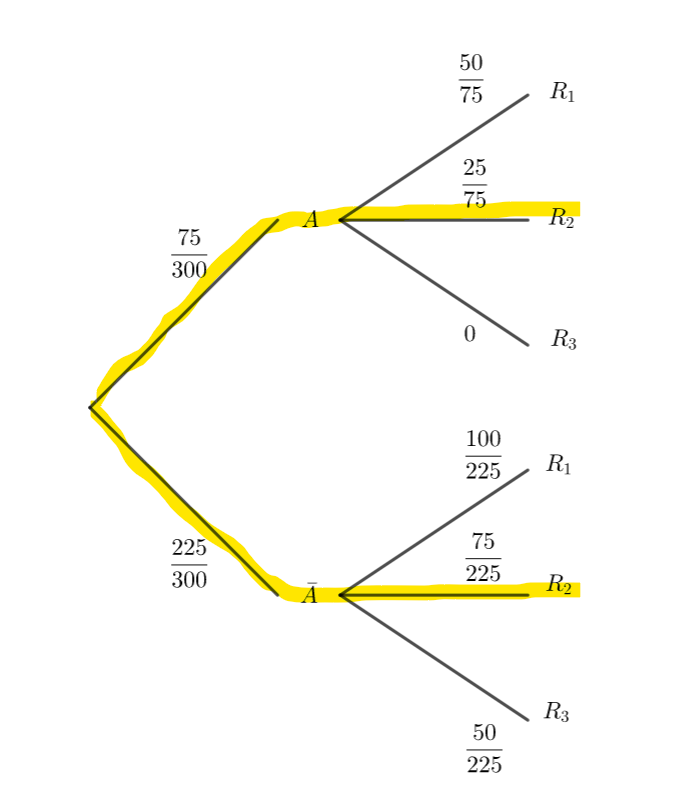
b. Montrer que la probabilité que la personne interrogée ait réussi l’examen à sa deuxième présentation est égale à \frac{1}{3}
c. La personne interrogée a réussi l’examen à sa deuxième présentation. Quelle est la probabilité qu’elle ait suivi une formation avec conduite accompagnée ?
3. On note X la variable aléatoire qui, à toute personne choisie au hasard dans le groupe, associe le nombre de fois où elle s’est présentée à l’examen jusqu’à sa réussite.
Ainsi, X=1 correspond à l’évènement R_1.
a. Déterminer la loi de probabilité de la variable aléatoire X.
b. Calculer l’espérance de cette variable aléatoire. Interpréter cette valeur dans le contexte de l’exercice
4. On choisit, successivement et de façon indépendante, n personnes parmi les 300 du groupe étudié, où n est un entier naturel non nul. On assimile ce choix à un tirage avec remise de n personnes parmi les 300 personnes du groupe.
On admet que la probabilité de l’évènement R_3 est égale à \frac{1}{6}.
a. Exprimer en fonction de n, la probabilité de l’évènement G: « au moins une personne a réussi l’examen à la troisième tentative ».
On considère la fonction Python seuil ci-dessous, où p est un nombre réel appartenant à l’intervalle ]0;1[.
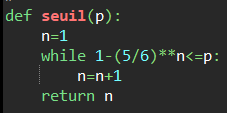
b. Quelle est la valeur renvoyée par la commande seuil(0,9) ? Interpréter cette valeur dans le contexte de l’exercice.
Exercice n°2
Dans une école de statistique, après étude des dossiers des candidats, le recrutement se fait de deux façons :
• 10 % des candidats sont sélectionnés sur dossier. Ces candidats doivent ensuite passer un
oral à l’issue duquel 60 % d’entre eux sont finalement admis à l’école.
• Les candidats n’ayant pas été sélectionnés sur dossier passent une épreuve écrite à l’issue
de laquelle 20 % d’entre eux sont admis à l’école.
Partie A
On choisit au hasard un candidat à ce concours de recrutement. On notera :
• D l’évènement « le candidat a été sélectionné sur dossier »;
• A l’évènement « le candidat a été admis à l’école »;
• \bar{D} et \bar{A} les évènements contraires des évènements D et A respectivement.
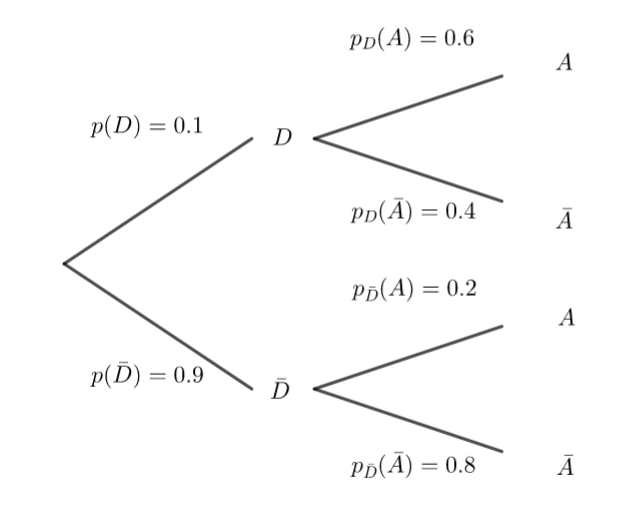
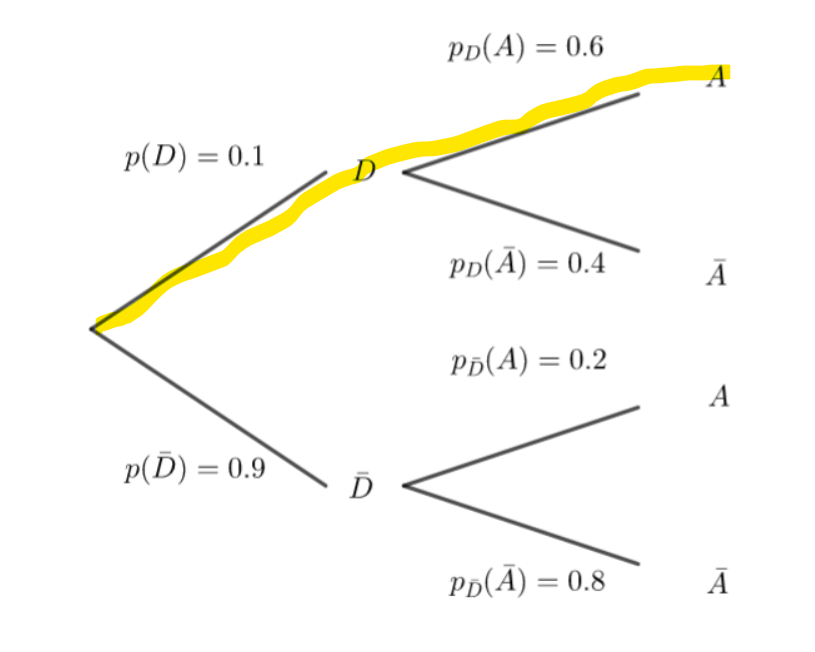
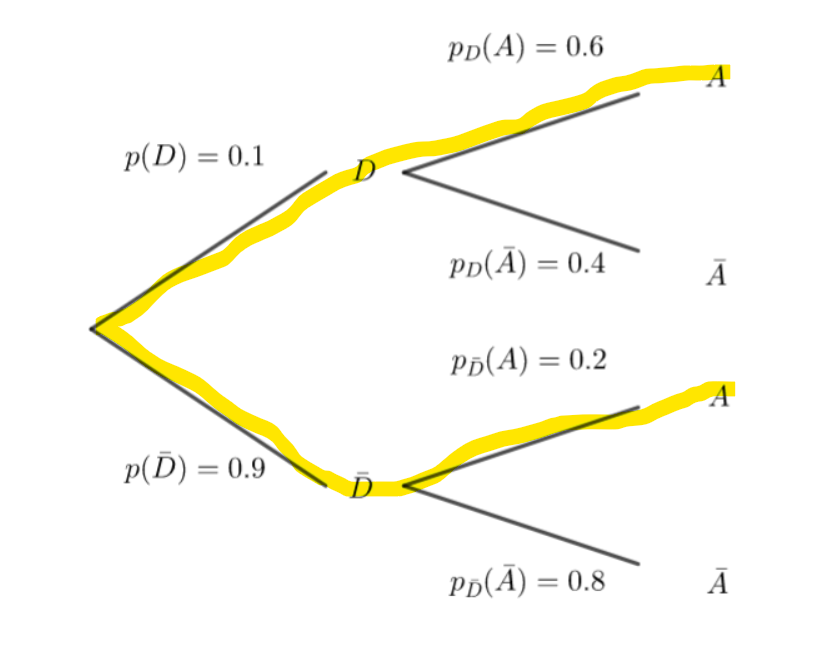
1. Traduire la situation par un arbre pondéré.
2. Calculer la probabilité que le candidat soit sélectionné sur dossier et admis à l’école.
3. Montrer que la probabilité de l’évènement A est égale à 0.24.
4. On choisit au hasard un candidat admis à l’école. Quelle est la probabilité que son dossier n’ait pas été sélectionné ?
Partie B
1. On admet que la probabilité pour un candidat d’être admis à l’école est égale à 0.24.
On considère un échantillon de sept candidats choisis au hasard, en assimilant ce choix à un tirage au sort avec remise. On désigne par X la variable aléatoire dénombrant les candidats admis à l’école parmi les sept tirés au sort.
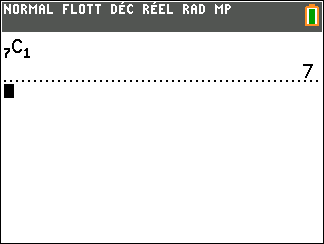
a. On admet que la variable aléatoire X suit une loi binomiale. Quels sont les paramètres de cette loi ?
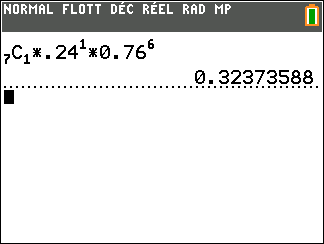
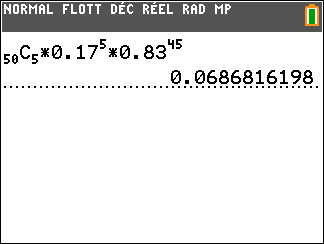
b. Calculer la probabilité qu’un seul des sept candidats tirés au sort soit admis à l’école.On donnera une réponse arrondie au centième.
c. A l’aide de la calculatrice, calculer la probabilité qu’au moins deux des sept candidats tirés au sort soient admis à cette école. On donnera une réponse arrondie au centième.
2. Un lycée présente n candidats au recrutement dans cette école, où n est un entier naturel
non nul.
On admet que la probabilité pour un candidat quelconque du lycée d’être admis à l’école est égale à 0.24 et que les résultats des candidats sont indépendants les uns des autres.
a. Donner l’expression, en fonction de n, de la probabilité qu’aucun candidat issu de ce lycée ne soit admis à l’école.
b. À partir de quelle valeur de l’entier n la probabilité qu’au moins un élève de ce lycée soit admis à l’école est-elle supérieure à 0.99 ?
Exercice n°3
Partie A
Une étude sur ce nouveau test donne les résultats suivants :
• si un athlète est dopé, la probabilité que le résultat du test soit positif est 0.98 (sensibilité du test);
• si un athlète n’est pas dopé, la probabilité que le résultat du test soit négatif est 0.995
(spécificité du test).
On fait subir le test à un athlète sélectionné au hasard au sein des participants à une compétition d’athlétisme.
On note D l’évènement « l’athlète est dopé » et T l’évènement « le test est positif ».
On admet que la probabilité de l’évènement D est égale à 0.08.
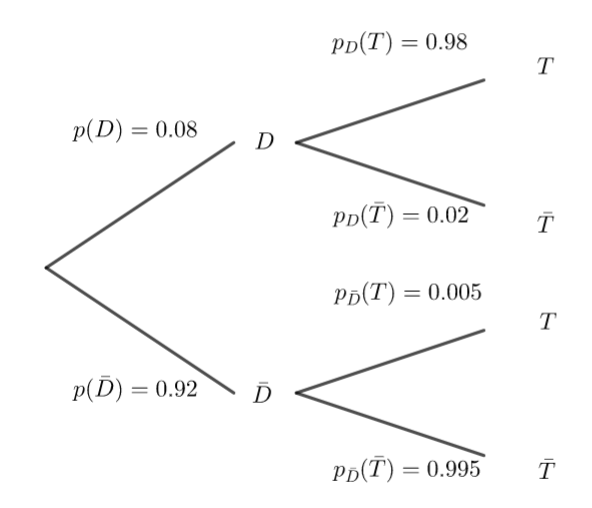
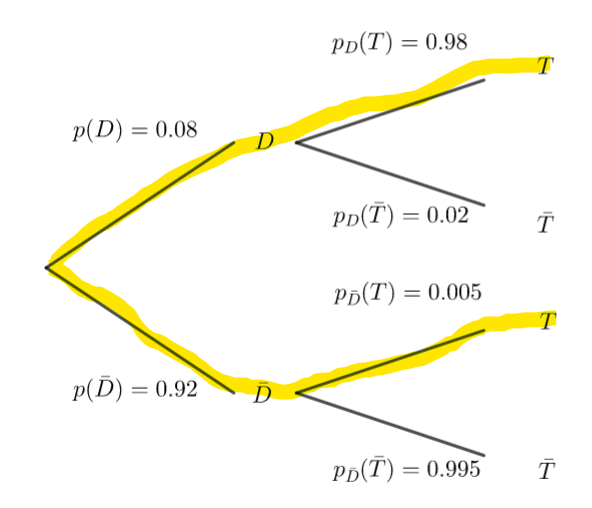
1. Traduire la situation sous la forme d’un arbre pondéré.
2. Démontrer que p(T)=0.083.
3. a. Sachant qu’un athlète présente un test positif, quelle est la probabilité qu’il soit dopé ?
3. b.Le laboratoire décide de commercialiser le test si la probabilité de l’évènement« un athlète présentant un test positif est dopé » est supérieure ou égale à 0.95.
Le test proposé par le laboratoire sera-t-il commercialisé? Justifier.
Partie B
Dans une compétition sportive, on admet que la probabilité qu’un athlète contrôlé présente un test positif est 0.103.
On suppose que les organisateurs décident de contrôler 5 athlètes au hasard parmi les athlètes de cette compétition.
On note X la variable aléatoire égale au nombre d’athlètes présentant un test positif parmi les 5 athlètes contrôlés.
1. Quelle est la nature de la loi suivie par la variable aléatoire X. Préciser ses paramètres.
2. Calculer l’espérance E(X) et interpréter le résultat dans le contexte de l’exercice.
Exercice n°4
Un test est mis au point pour détecter une maladie dans un pays.
Selon les autorités sanitaires de ce pays, 7 % des habitants sont infectés par cette maladie.
Parmi les individus infectés, 20 % sont déclarés négatifs.
Parmi les individus sains, 1 % sont déclarés positifs.
Une personne est choisie au hasard dans la population.
On note :
• M l’évènement : « la personne est infectée par la maladie »;
• T l’évènement : « le test est positif ».
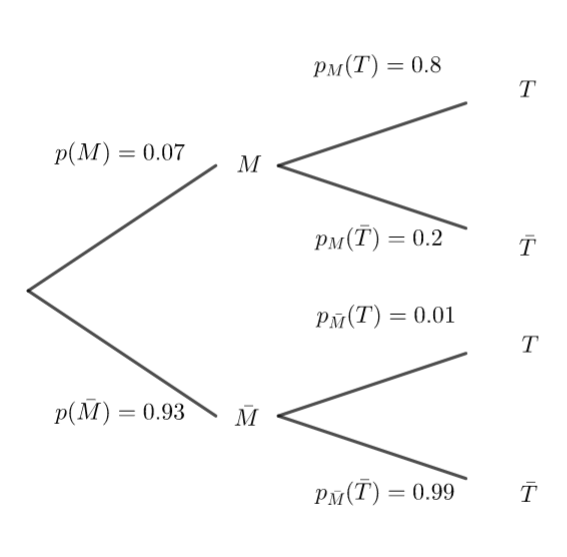
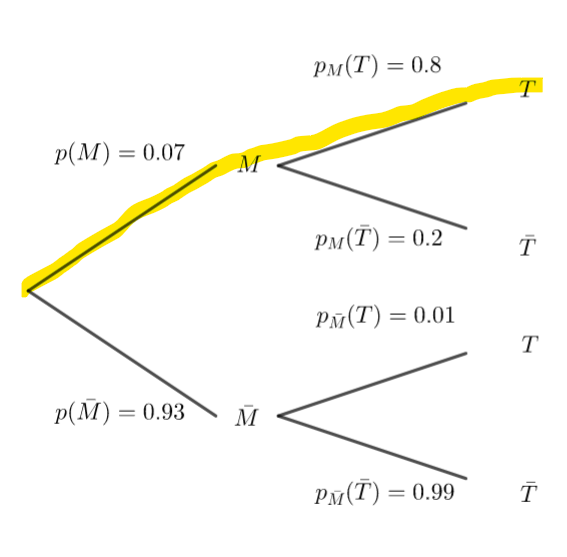
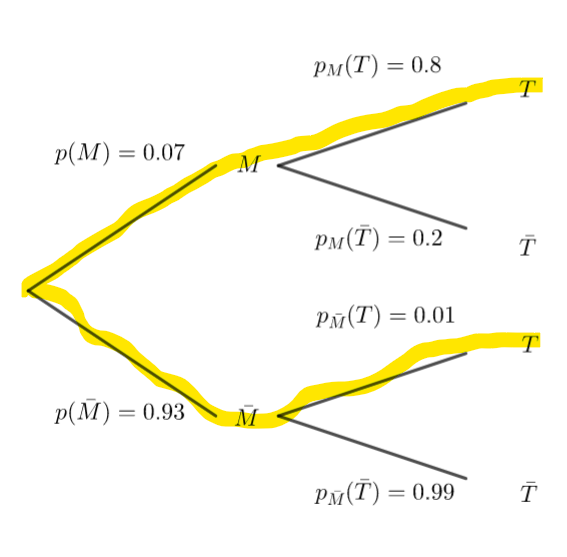
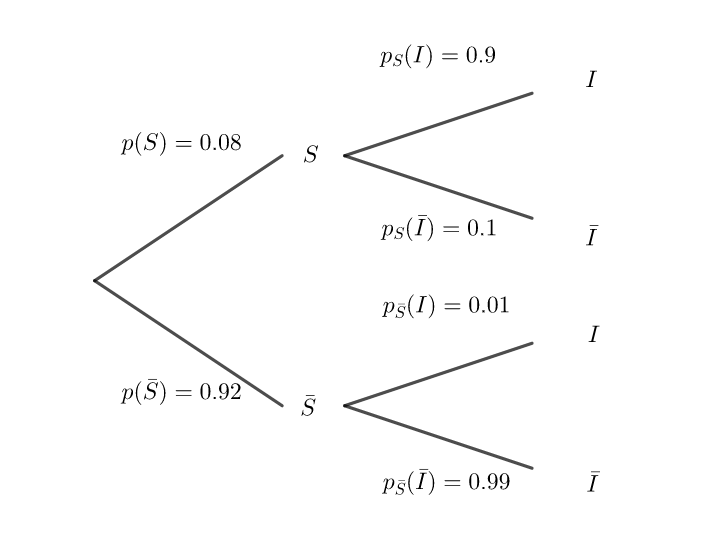
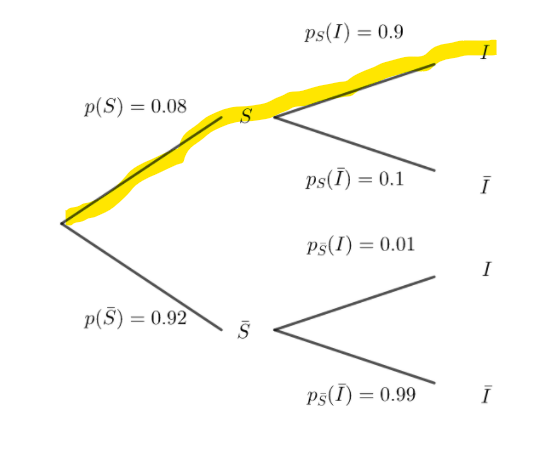
1. Construire un arbre pondéré modélisant la situation proposée.
2. a. Quelle est la probabilité pour que la personne soit infectée par la maladie et que
son test soit positif ?
2.b. Montrer que la probabilité que son test soit positif est de 0.0653.
3. On sait que le test de la personne choisie est positif.
Quelle est la probabilité qu’elle soit infectée ?
On donnera le résultat sous forme approchée à 10^{-2} près.
4. On choisit dix personnes au hasard dans la population. La taille de la population de ce
pays permet d’assimiler ce prélèvement à un tirage avec remise.
On note X la variable aléatoire qui comptabilise le nombre d’individus ayant un test
positif parmi les dix personnes.
a. Quelle est la loi de probabilité suivie par X ? Préciser ses paramètres.
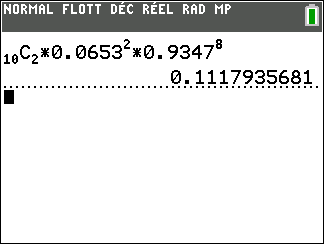
b. Déterminer la probabilité pour qu’exactement deux personnes aient un test positif.
On donnera le résultat sous forme approchée à 10^{-2} près.
5. Déterminer le nombre minimum de personnes à tester dans ce pays pour que la probabilité qu’au moins une de ces personnes ait un test positif, soit supérieure à 99 %.
Exercice n°5
Un sac contient les huit lettres suivantes : A B C D E F G H (2 voyelles et 6 consonnes).
Un jeu consiste à tirer simultanément au hasard deux lettres dans ce sac.
On gagne si le tirage est constitué d’une voyelle et d’une consonne.
1. Un joueur extrait simultanément deux lettres du sac.
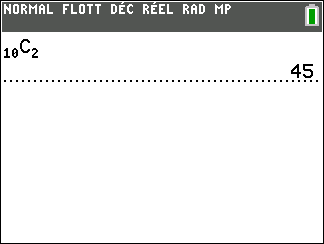
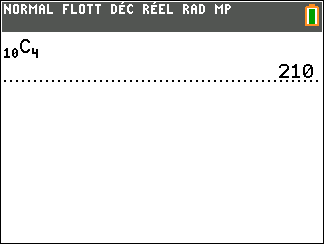
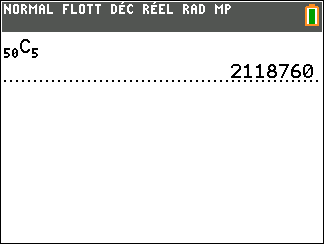
a. Déterminer le nombre de tirages possibles
b. Déterminer la probabilité que le joueur gagne à ce jeu.
Pour la suite de l’exercice, on admet que la probabilité que le joueur gagne est égale à \frac{3}{7}.
2. Pour jouer, le joueur doit payer k euros, k désignant un entier naturel non nul.
Si le joueur gagne, il remporte la somme de 10 euros, sinon il ne remporte rien.
On note G la variable aléatoire égale au gain algébrique d’un joueur (c’est-à-dire la
somme remportée à laquelle on soustrait la somme payée).
a. Déterminer la loi de probabilité de G.
b. Quelle doit être la valeur maximale de la somme payée au départ pour que le jeu reste favorable au joueur ?
3. Dix joueurs font chacun une partie. Les lettres tirées sont remises dans le sac après
chaque partie.
On note X la variable aléatoire égale au nombre de joueurs gagnants.
a. Justifier que X suit une loi binomiale et donner ses paramètres
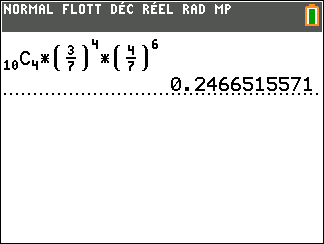
b. Calculer la probabilité, arrondie à 10^{-3} , qu’il y ait exactement quatre joueurs gagnants
c. Calculer p(X\geq 5) en arrondissant à 10^{-3}.
Exercice n°6
Dans tout cet exercice, les probabilités seront arrondies, si nécessaire, à 10^{-3} .
D’après une étude, les utilisateurs réguliers de transports en commun représentent 17 % de la population française.
Parmi ces utilisateurs réguliers, 32 % sont des jeunes âgés de 18 à 24 ans.
Partie A :
On interroge une personne au hasard et on note :
• R l’évènement : « La personne interrogée utilise régulièrement les transports en
commun ».
• J l’évènement : « La personne interrogée est âgée de 18 à 24 ans ».
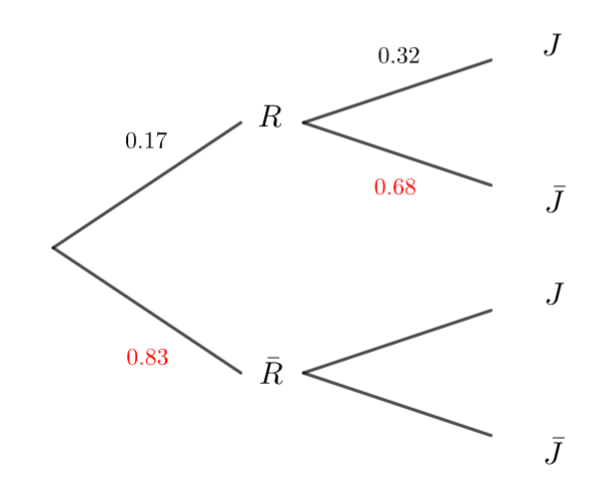
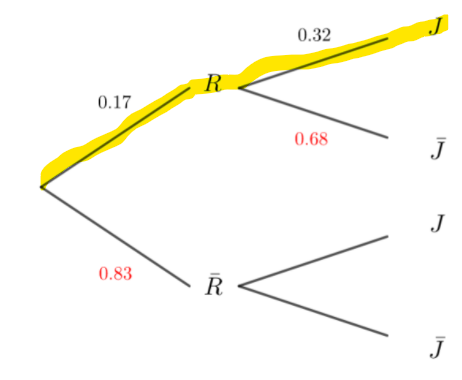
1. Représentez la situation à l’aide de cet arbre pondéré en y reportant les données de l’énoncé.
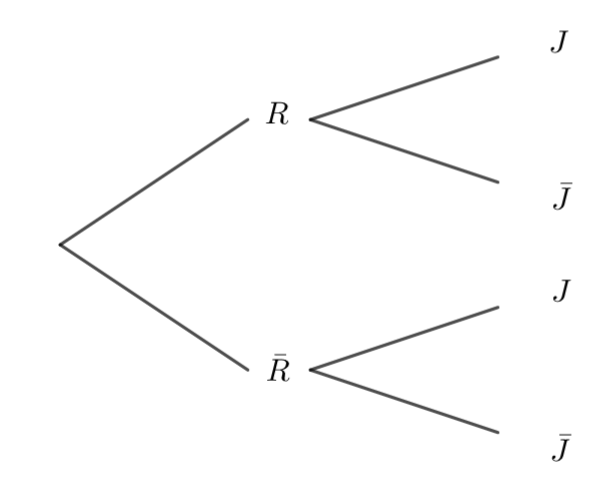
2. Calculer la probabilité p(R\cap J) .
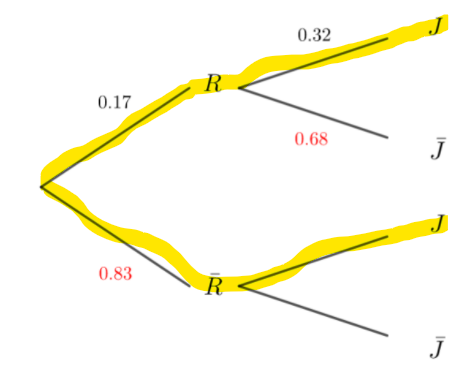
3. D’après cette même étude, les jeunes de 18 à 24 ans représentent 11 % de la population française.
Montrer que la probabilité que la personne interrogée soit un jeune de 18 à 24 ans n’utilisant pas régulièrement les transports en commun est 0.056 à 10^{-3} près
4. En déduire la proportion de jeunes de 18 à 24 ans parmi les utilisateurs non réguliers des transports en commun.
Partie B :
Lors d’un recensement sur la population française, un recenseur interroge au hasard 50 personnes en une journée sur leur pratique des transports en commun.
La population française est suffisamment importante pour assimiler ce recensement à
un tirage avec remise.
Soit X la variable aléatoire dénombrant les personnes utilisant régulièrement les transports en commun parmi les 50 personnes interrogées.
1. Déterminer, en justifiant, la loi de X et préciser ses paramètres.
2. Calculer p(X=5) et interpréter le résultat.
3. Le recenseur indique qu’il y a plus de 95 % de chance pour que, parmi les 50 personnes interrogées, moins de 13 d’entre elles utilisent régulièrement les transports
en commun.
Cette affirmation est-elle vraie ? Justifier votre réponse.
4. Quel est le nombre moyen de personnes utilisant régulièrement les transports en
commun parmi les 50 personnes interrogées ?
Exercice n°7
Une entreprise reçoit quotidiennement de nombreux courriels (courriers électroniques).
Parmi ces courriels, 8 % sont du « spam », c’est-à-dire des courriers à intention publicitaire,
voire malveillante, qu’il est souhaitable de ne pas ouvrir.
On choisit au hasard un courriel reçu par l’entreprise.
Les propriétés du logiciel de messagerie utilisé dans l’entreprise permettent d’affirmer que :
• La probabilité que le courriel choisi soit classé comme « indésirable » sachant que c’est
un spam est égale à 0,9.
• La probabilité que le courriel choisi soit classé comme « indésirable » sachant que ce
n’est pas un spam est égale à 0,01.
On note :
• S l’évènement « le courriel choisi est un spam »;
• I l’évènement « le courriel choisi est classé comme indésirable par le logiciel de messagerie ».
• S et I les évènements contraires de S et I respectivement.
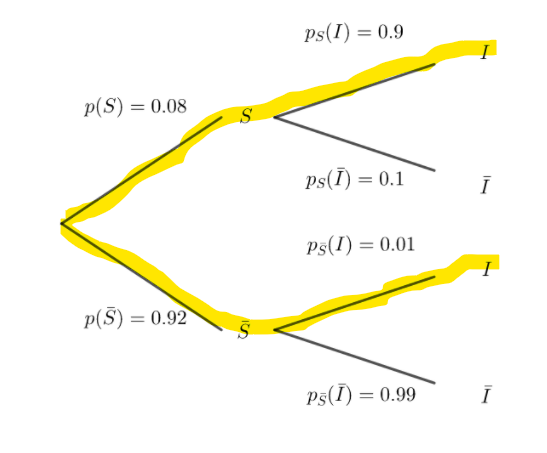
1. Modéliser la situation étudiée par un arbre pondéré, sur lequel on fera apparaître les
probabilités associées à chaque branche.
2. a. Démontrer que la probabilité que le courriel choisi soit un message de spam et
qu’il soit classé indésirable est égale à 0,072.
b. Calculer la probabilité que le message choisi soit classé indésirable
c. Le message choisi est classé comme indésirable. Quelle est la probabilité que ce soit effectivement un message de spam ? On donnera un résultat arrondi au centième.
3. On choisit au hasard 50 courriels parmi ceux reçus par l’entreprise. On admet que ce choix se ramène à un tirage au hasard avec remise de 50 courriels parmi l’ensemble des courriels reçus par l’entreprise.
On appelle Z la variable aléatoire dénombrant les courriels de spam parmi les 50 choisis.
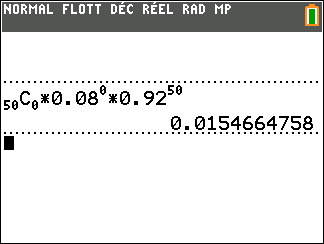
a. Quelle est la loi de probabilité suivie par la variable aléatoire Z, et quels sont ses paramètres ?
b. Quelle est la probabilité que, parmi les 50 courriels choisis, au moins un soit un spam ? On donnera un résultat arrondi au centième.