Sommaire
Exercice n°1
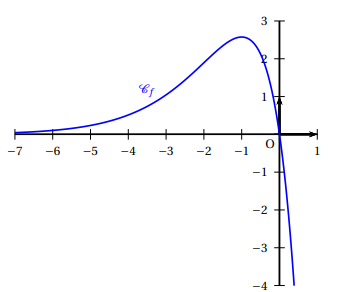
On considère la fonction f définie sur \mathbf{R} par
f(x)=-7xe^xCette fonction admet sur R une dérivée f’ et une dérivée seconde f".
On donne ci-contre la courbe C_f représentative de la fonction f .
Une seule des quatre réponses proposées est exacte, trouvez-la.
a. f’ est positive sur l’intervalle [-6;0].
b. f est convexe sur l’intervalle [-1;0].
c. C_f admet un point d’inflexion pour x=-1.
d. f" change de signe en x=-2.
Exercice n°2
On donne ci-dessous la courbe C_g représentant une fonction g définie sur [0;2].
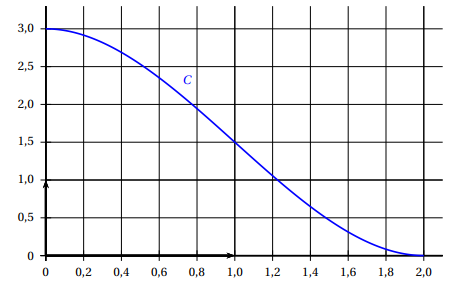
Une seule des quatre réponses proposées est exacte, trouvez-la.
a. g est concave sur l’intervalle [0;2].
b. g"(x)\geq 0 pour x\in [0;2].
c. C_g admet un point d’inflexion sur l’intervalle [0;2].
d. g'(1)>0.
Exercice n°3
On considère la fonction f définie et dérivable sur \mathbf{R}. Sa dérivée f’ est aussi dérivable sur \mathbf{R}
La courbe ci-contre
représente la dérivée seconde f".
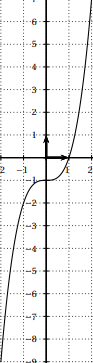
Une seule des quatre réponses proposées est exacte, trouvez-la.
a. f est convexe sur l’intervalle [-2;2].
b. f est concave sur l’intervalle [-2;2].
c. C_f admet un point d’inflexion sur l’intervalle [-2;2].
d. f’ est croissante sur l’intervalle [-2;2].
Exercice n°4
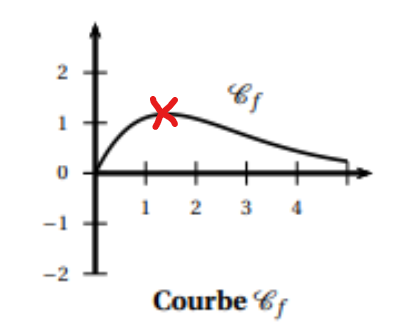
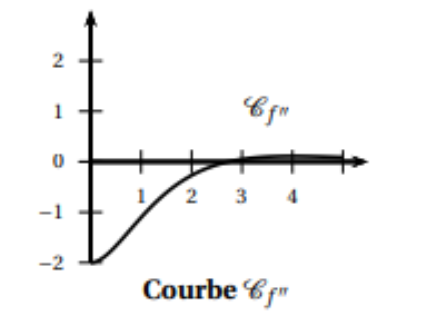
On donne ci-dessous la courbe C_f représentative dans un repère donné d’une fonction f définie et dérivable sur l’intervalle [0;5] ainsi que les courbes représentatives C_f’ et C_f" respectivement de la dérivée f’ et de la dérivée seconde f" de la fonction f .
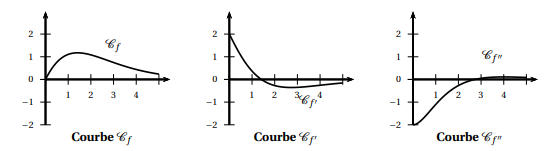
Dans cette partie les réponses seront obtenues à l’aide de lectures graphiques.
1. Donner un encadrement par deux entiers consécutifs du nombre réel pour lequel la fonction f
semble atteindre son maximum.
2. a. Donner un intervalle défini par deux entiers sur lequel la fonction fsemble convexe.
b. Expliquer pourquoi on peut conjecturer que la courbe C_f admet un point d’inflexion.
Donner un encadrement par deux entiers consécutifs de l’abscisse de ce point d’inflexion.
Exercice n°5
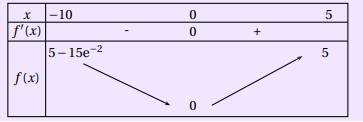
On considère la fonction f définie et dérivable sur [-10;5] par f(x)=(x-5)e^{0.2x}+5
- On note f’ sa dérivée sur [-10;5]
a. Montrer que f'(x)=0.2xe^{0.2x}
b. Dresser le tableau de variation de la fonction f définie [-10;5].
c. Déterminer la valeur exacte du coefficient directeur de la tangente T_{-5} à C_f au point A d’abscisse -5 .
2. a. Montrer que f"(x)=(0.2+0.04x)e^{0.2x}
2. b. Etudier la convexité de f sur [-10;5]
Exercice n°6
On considère la fonction f définie et dérivable sur [0;30] par f(x)=x^3-39x^2+315x+45
On note C_f sa courbe représentative.
Une seule des quatre réponses proposées est exacte, trouvez-la.
a. f est convexe sur l’intervalle [0;30].
b. f est concave sur l’intervalle [5;21].
c. C_f admet un point d’inflexion au point d’abscisse 13.
d. f’ est croissante sur l’intervalle [0;5] et sur [21;30].
Exercice n°7
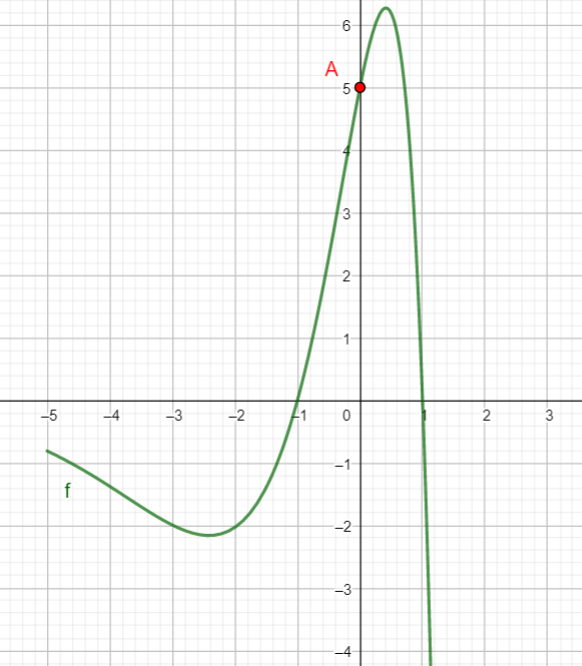
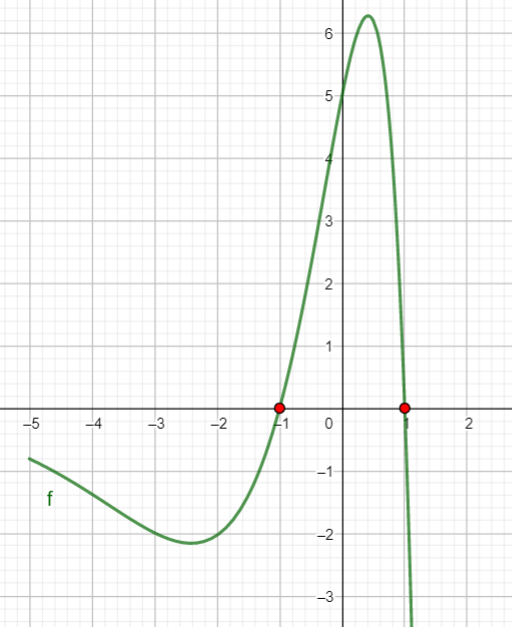
On considère la fonction f définie et dérivable sur \mathbf{R} par f(x)=(-5x^2+5)e^x
Cette fonction admet sur R une dérivée f’ et une dérivée seconde f".
On donne ci-contre la courbe C_f représentative de la fonction f.
1. a. Calculer les coordonnées du point A , intersection de la courbe C_f avec l’axe des ordonnées. Placer le point A dans le repère ci-dessus.
b. Déterminer par le calcul les coordonnées des points d’intersection de C_f et de l’axe des abscisses. Puis les placer dans le repère ci-dessus.
c. Montrer que pour tout x ∈ R, f'(x)=(-5x^2-10x+5)e^x
d. Étudier les variations de la fonction f sur l’intervalle [-5;2].
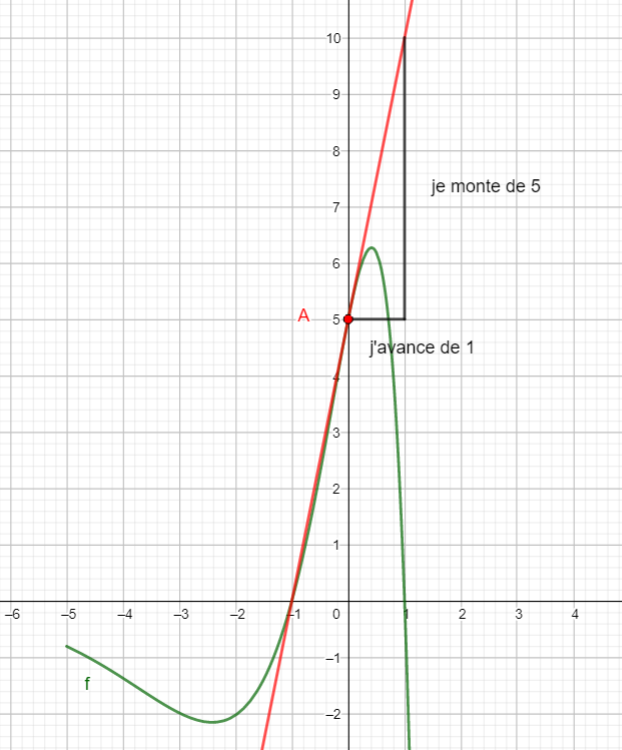
2. Soit \Delta la tangente à C_f au point d’abscisse 0.
a. Montrer qu’une équation de \Delta est y=5x+5
b. Tracer la droite \Delta dans le repère ci-dessus.
3. a Montrer que f"(x)=(-5x^2-20x-5)e^x.
b. Étudier la convexité de la fonction f sur l’intervalle [-5;2]
Exercice n°8
On appelle fonction « satisfaction » toute fonction dérivable qui prend ses valeurs entre 0 et 100 .
Lorsque la fonction « satisfaction » atteint la valeur 100, on dit qu’il y a « saturation ».
On définit aussi la fonction « envie » comme la fonction dérivée de la fonction « satisfaction ». On dira
qu’il y a « souhait » lorsque la fonction « envie » est positive ou nulle et qu’il y a « rejet » lorsque la
fonction « envie » est strictement négative.
Dans chaque partie, on teste un modèle de fonction « satisfaction » différent.
Les parties A, B et C sont indépendantes.
Partie A
Un étudiant prépare un concours, pour lequel sa durée de travail varie entre 0 et 6 heures par jour. Il modélise sa satisfaction en fonction de son temps de travail quotidien par la fonction « satisfaction » f dont la courbe représentative est donnée ci-dessous (x est exprimé en heures).
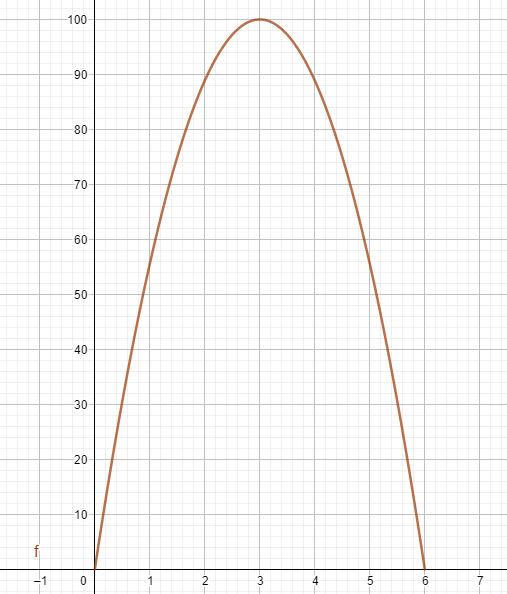
1. Lire graphiquement la durée de travail quotidien menant à « saturation ».
2. Déterminer à l’aide du graphique, à partir de quelle durée de travail il y a « rejet ».
Partie B
Le directeur d’une agence de trekking modélise la satisfaction de ses clients en fonction de la durée
de leur séjour. On admet que la fonction « satisfaction » g est définie sur l’intervalle [0;30] par g(x)=12.5xe^{-0.125x+1} (x est exprimé en jour).
1. Démontrer que, pour tout x de l’intervalle [0;30] , g'(x)=(12.5-1.5625x)e^{-0.125x+1}.
2. Étudier le signe de g'(x) sur l’intervalle [0;30] puis dresser le tableau des variations de g sur cet intervalle.
3. Quelle durée de séjour correspond-elle à l’effet « saturation » ?
Partie C
La direction des ressources humaines d’une entreprise modélise la satisfaction d’un salarié en fonction du salaire annuel qu’il perçoit. On admet que la fonction « satisfaction » h, est définie sur l’intervalle [0;50] par
h(x)=\frac{90}{1+e^{-0.25x+6}} (x est exprimé en millier d’euros).
La courbe C_h de la fonction h est représentée dans la fenêtre active Géogébra ci-dessous :
Un logiciel de calcul formel donne les résultats suivants :

1. Donner sans justification une expression de h"(x).
2. Résoudre dans l’intervalle [10;50] l’inéquation e^{-0.25x+6}-1>0.
3. En déduire la convexité de la fonction h sur l’intervalle [10;50].
4. À partir de quel salaire annuel peut-on estimer que la fonction « envie » décroît ? Justifier
5. Déterminer, en le justifiant, pour quel salaire annuel la fonction « satisfaction » atteint 80.
Arrondir au millier d’euros.