Sommaire
Exercice n°1 : 15 mars 2021 Sujet 1
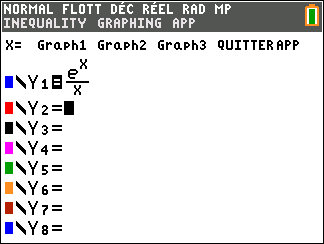
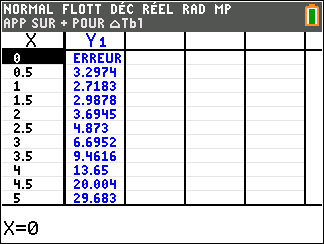
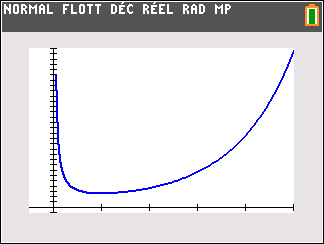
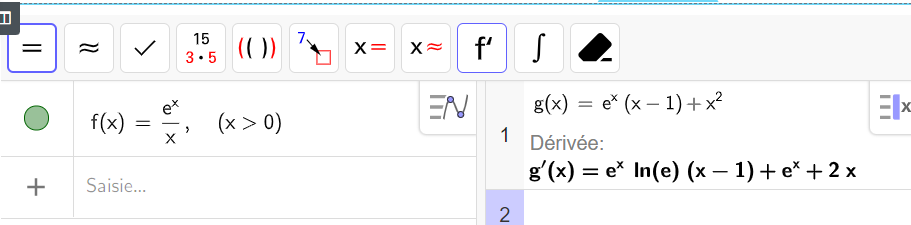
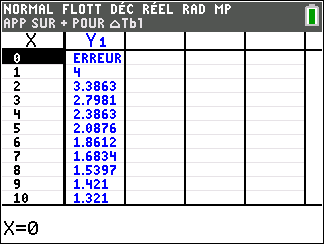
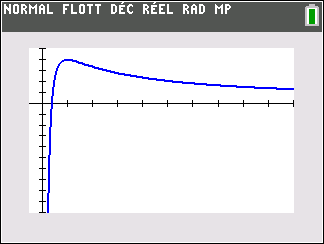
Soit f la fonction définie sur l’intervalle ]0;+\infty[ par : f(x)=\frac{e^x}{x}
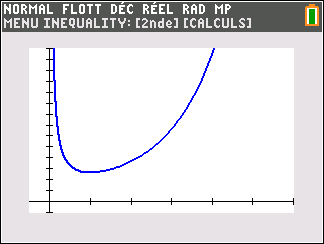
On note C_f la courbe représentative de la fonction f dans un repère orthonormé.
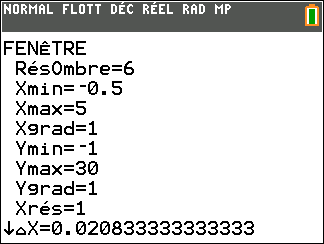
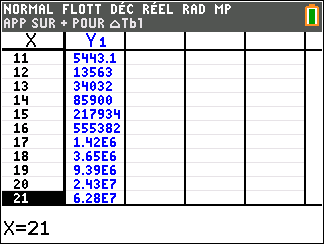
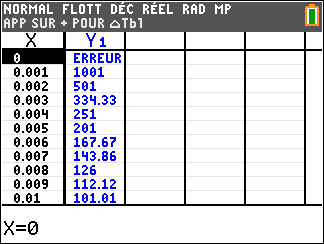
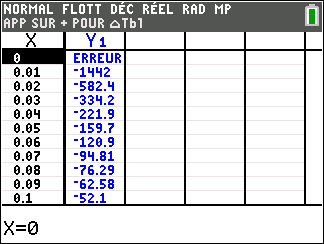
Avant de commencer l’exercice, il est bon de programmer sa TI 83 Premium CE.
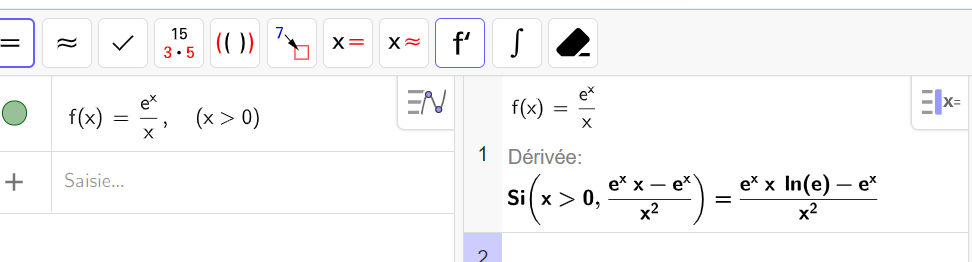
Au cours de l’exercice, on peut aussi utiliser la fenêtre active Géogébra ci-dessous pour conjecturer ou valider. Elle est composée de trois colonnes : la colonne à gauche est la colonne Algèbre, celle de milieu permet de faire du calcul formel ( calcul de dérivée, développer, factoriser, résoudre,…) et celle de droite correspond au graphique.
1. a. Préciser la limite de la fonction f en +\infty.
b. Justifier que l’axe des ordonnées est asymptote à la courbe C_f.
2. Montrer que, pour tout nombre réel x de l’intervalle ]0;+\infty[, on a : f'(x)=\frac{e^x(x-1)}{x^2}
où f’désigne la fonction dérivée de la fonction f.
3. Déterminer les variations de la fonction f sur l’intervalle ]0;+\infty[.
On établira un tableau de variations de la fonction f dans lequel apparaîtront les limites
4. Soit m un nombre réel. Préciser, en fonction des valeurs du nombre réel m, le nombre de solutions de l’équation f(x)=m.
5. On note \Delta la droite d’équation y=-x.
On note A un éventuel point de C_f d’abscisse a en lequel la tangente à la courbe C_f est parallèle à la droite \Delta.
a. Montrer que a est solution de l’équation e^x(x-1)+x^2=0.
On note g la fonction définie sur [0;+\infty[par g(x)=e^x(x-1)+x^2
On admet que la fonction g est dérivable et on note g’ sa fonction dérivée
b. Calculer g'(x) pour tout nombre réel x de l’intervalle [0;+\infty[, puis dresser le tableau de variations de g sur [0;+\infty[.
c. Montrer qu’il existe un unique point A en lequel la tangente à C_f est parallèle à la droite \Delta.
Exercice n°2 : Session 15 mars 2021 Sujet 2
Partie I : Étude d’une fonction auxiliaire
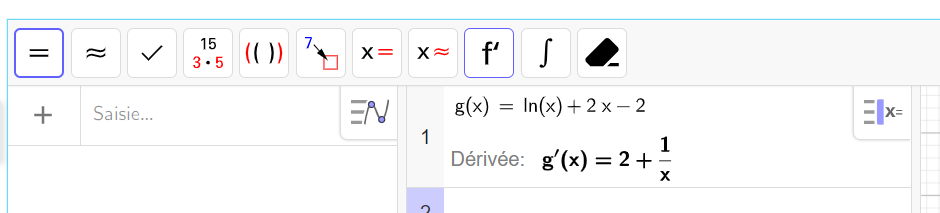
Soit g la fonction définie sur l’intervalle ]0;+\infty[ par : g(x)=ln(x)+2x-2
Avant de commencer l’exercice, il est bon de programmer sa TI 83 Premium CE.
Au cours de l’exercice, on peut aussi utiliser la fenêtre active Géogébra ci-dessous pour conjecturer ou valider. Elle est composée de trois colonnes : la colonne à gauche est la colonne Algèbre, celle de milieu permet de faire du calcul formel ( calcul de dérivée, développer, factoriser, résoudre,…) et celle de droite correspond au graphique. A vous de saisir les fonctions dans la colonne de gauche.
1. Déterminer les limites de g en +\infty et 0.
2. Déterminer le sens de variation de la fonction g sur l’intervalle ]0;+\infty[.
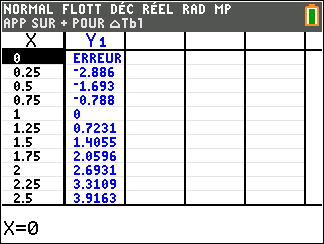
3. Démontrer que l’équation g(x)=0 admet une unique solution \alpha sur l’intervalle ]0;+\infty[ (on dressera d’abord le tableau de variations de g sur ]0;+\infty[).
4. Calculer g(1) puis déterminer le signe de g sur ]0;+\infty[.
Partie II : Étude d’une fonction f
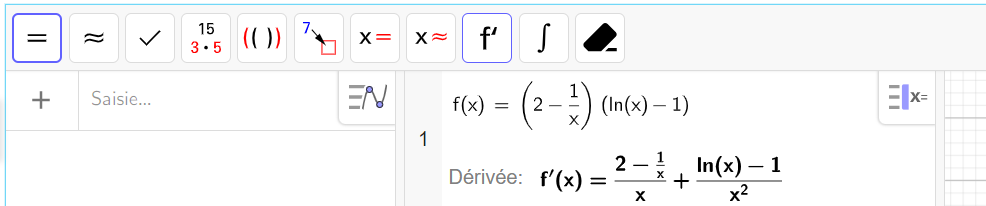
On considère la fonction f la fonction définie sur l’intervalle ]0;+\infty[ par : f(x)=(2-\frac{1}{x})(ln(x)-1).
1. a. On admet que la fonction f est dérivable sur l’intervalle ]0;+\infty[ et on note f’ sa dérivée.
Démontrer que, pour tout x de l’intervalle ]0;+\infty[, on a :
f'(x)=\frac{g(x)}{x^2}.
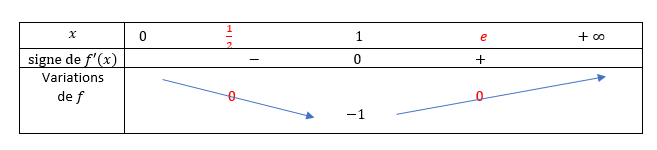
b. Dresser le tableau de variation de la fonction f sur l’intervalle ]0;+\infty[. Le calcul des limites n’est pas demandé.
2. Résoudre l’équation f(x)=0 sur l’intervalle ]0;+\infty[ puis dresser le tableau de signes de f sur l’intervalle ]0;+\infty[.
Partie III : Étude d’une fonction F admettant pour dérivée la fonction f
On admet qu’il existe une fonction F dérivable sur ]0;+\infty[ dont la dérivée F’est égale à la fonction f.
Ainsi, on a : F’=f.
On note C_F la courbe représentative de la fonction F dans un repère orthonormé . On
ne cherchera pas à déterminer une expression de F(x).
1. Étudier les variations de F sur ]0;+\infty[.
2. La courbe C_F représentative de F admet-elle des tangentes parallèles à l’axe des abscisses ?
Justifier la réponse.
Exercice n°3 : Amérique du Nord mai 2021
Dans le plan muni d’un repère, on considère ci-dessous la courbe C_f représentative d’une
fonction f , deux fois dérivable sur l’intervalle ]0;+\infty[.
La courbe C_f admet une tangente horizontale T au point A(1;4).
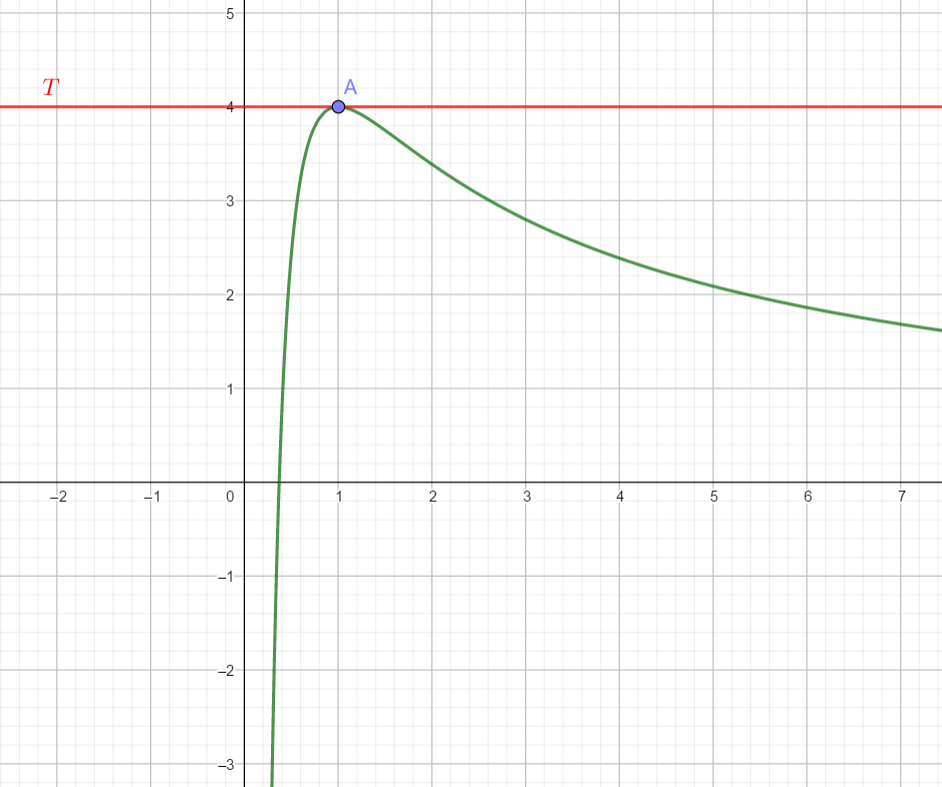
1. Préciser les valeurs f(1) et f'(1).
On admet que la fonction f est définie pour tout réel x de l’intervalle ]0;+\infty[ par :
f(x)=\frac{a+bln(x)}{x}
où a et b sont deux nombres réels.
2. Démontrer que, pour tout réel x strictement positif, on a :
f'(x)=\frac{b-a-bln(x)}{x^2}
3. En déduire les valeurs des réels a et b.
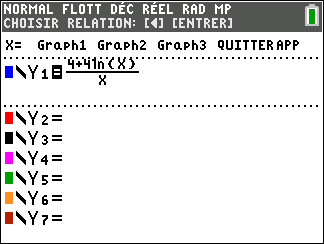
Dans la suite de l’exercice, on admet que la fonction f est définie sur l’intervalle ]0;+\infty[ par : f(x)=\frac{4+4ln(x)}{x}
Avant de poursuivre l’exercice, il est bon de programmer sa TI 83 Premium CE.
4. Déterminer les limites de la fonction f en 0^{+} et en +\infty.
5. Déterminer le tableau de variations de f sur l’intervalle ]0;+\infty[.
6. Démontrer que, pour tout réel x strictement positif, on a :
f"(x)=\frac{-4+8ln(x)}{x^3}.
7. Montrer que la courbe C_f possède un unique point d’inflexion B dont on précisera les coordonnées.
Exercice n°4 : Baccalauréat Polynésie 2 juin 2021 exercice A
Cet exercice est composé de trois parties indépendantes.
On a représenté ci-dessous, dans un repère orthonormé, une portion de la courbe représentative C_f d’une fonction f définie sur \mathbf{R} :
Dans le plan muni d’un repère, on considère ci-dessous la courbe C_f représentative d’une
fonction f , deux fois dérivable sur l’intervalle ]0;+\infty[.
La courbe C_f admet une tangente horizontale T au point A(1;4).
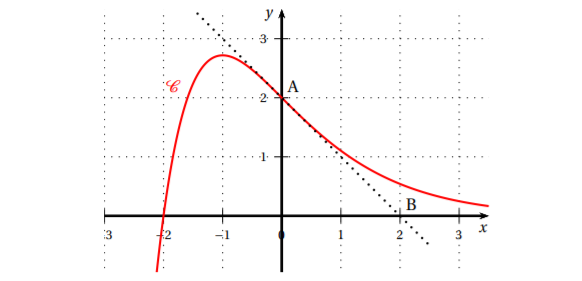
On considère les points A(0;2) et B(2;0).
Partie 1
Sachant que la courbe C_f passe par A et que la droite (AB) est la tangente à la courbe C_f au point A, donner par lecture graphique :
1. La valeur de f(0) et celle de f'(0).
2. Un intervalle sur lequel la fonction f semble convexe.
Partie 2
On note (E) l’équation différentielle y’=-y+e^{-x}.
On admet que g: x\to xe^{-x} est une solution particulière de (E).
1. Donner toutes les solutions sur \mathbf{R} de l’équation différentielle (H):y’=-y.
2. En déduire toute les solutions sur \mathbf{R} de l’équation différentielle (E).
3. Sachant que la fonction f est la solution particulière de (E)qui vérifie f(0)=2, déterminer une expression de f(x) en fonction de x.
Partie 3
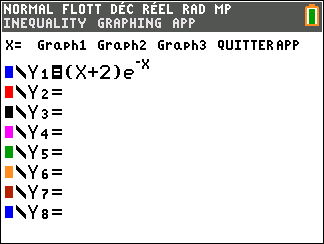
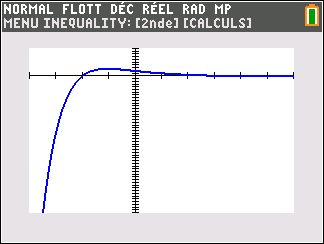
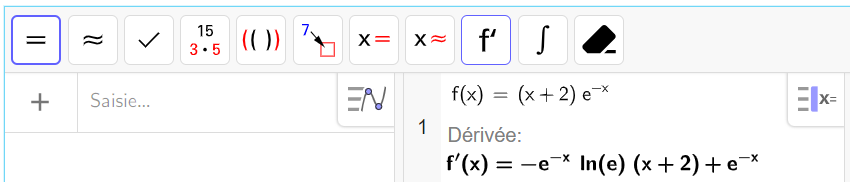
On admet que pour tout nombre réel x , f(x)=(x+2)e^{-x}.
Avant de commencer l’exercice, il est bon de programmer sa TI 83 Premium CE.A REFAIRE
1. On rappelle que f’ désigne la fonction dérivée de la fonction f.
a. Montrer que pour tout nombre réel x , f'(x)=(-x-1)e^{-x}.
b. Étudier le signe de f'(x) sur \mathbf{R} et dresser le tableau des variations de f sur \mathbf{R}.
On ne précisera ni la limite de f en -\infty ni la limite de f en +\infty.
On calculera la valeur exacte de l’extremum de f sur \mathbf{R}.
2. On rappelle que f" désigne la fonction dérivée seconde de la fonction f.
a. Calculer f"(x)pour tout x \in \mathbf{R}.
b. Peut-on affirmer que f est convexe sur l’intervalle [0;+\infty[?
Exercice n°5 : Baccalauréat Polynésie 2 juin 2021 exercice B
Cet exercice est composé de deux parties.
Certains résultats de la première partie seront utilisés dans la deuxième.
Partie 1 : Étude d’une fonction auxiliaire
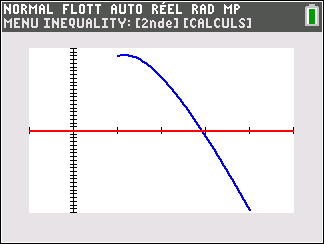
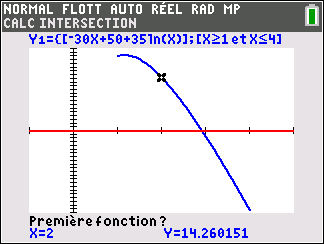
Soit la fonction f définie sur l’intervalle [1;4] par :
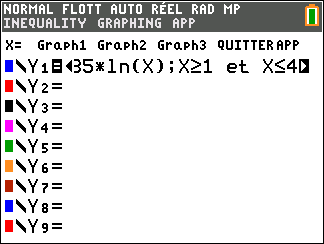
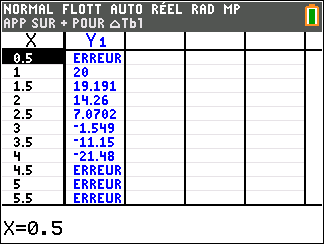
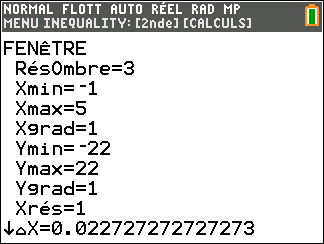
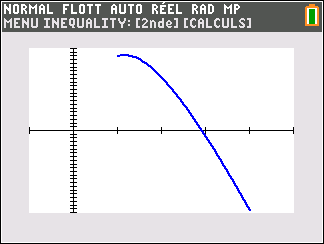
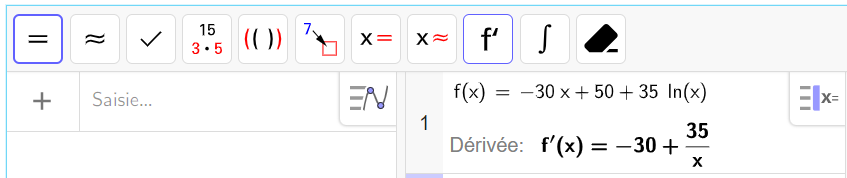
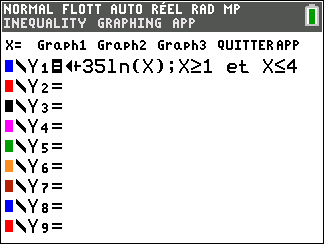
f(x)=-30x+50+35ln(x)
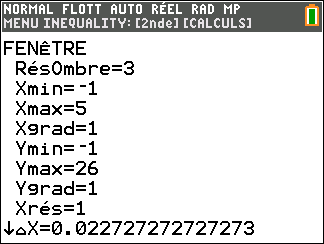
Avant de commencer l’exercice, il est bon de programmer sa TI 83 Premium CE.
Au cours de l’exercice, on peut aussi utiliser la fenêtre active Géogébra ci-dessous pour conjecturer ou valider. Elle est composée de trois colonnes : la colonne à gauche est la colonne Algèbre, celle de milieu permet de faire du calcul formel ( calcul de dérivée, développer, factoriser, résoudre,…) et celle de droite correspond au graphique. A vous de saisir les fonctions dans la colonne de gauche.
1. On rappelle que f’ désigne la fonction dérivée de la fonction f.
a. Pour tout nombre réel x de l’intervalle [1;4], montrer que :
f'(x)=\frac{35-30x}{x}.
b. Déterminer le signe de f'(x) sur l’intervalle [1;4].
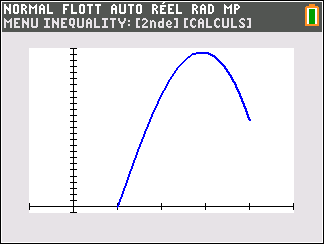
c. En déduire le tableau de variations de f sur l’intervalle [1;4].
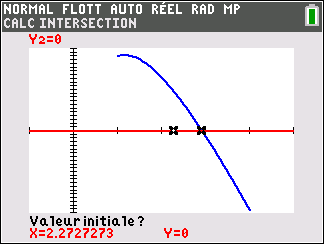
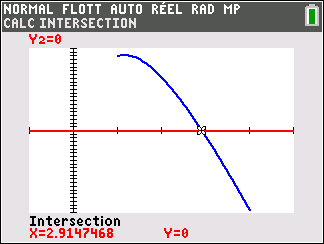
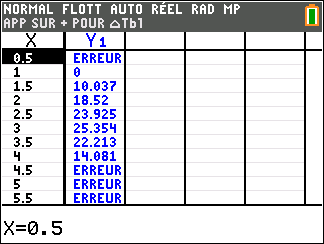
2. Justifier que l’équation f(x)=0 admet une unique solution, notée \alpha, sur l’intervalle [1;4] puis donner une valeur approchée de \alpha à 10^{-3} près.
3. Dresser le tableau de signe de f(x) sur [1;4].
Partie 2 : Optimisation
Une entreprise vend du jus de fruits. Pour x milliers de litres vendus, avec x appartenant à l’intervalle [1;4], l’analyse des ventes conduit à modéliser le bénéfice B(x) par l’expression donnée en milliers d’euros par :
B(x)=-15x^2+15x+35xln(x)
Avant de commencer l’exercice, il est bon de programmer sa TI 83 Premium CE.A
1. D’après le modèle, calculer le bénéfice réalisé par l’entreprise lorsqu’elle vend 2500 litres de jus de fruits.
On donnera une valeur approchée à l’euro près de ce bénéfice.
2. Pour tout x de l’intervalle [1;4], montrer que B'(x)=f(x) où B’ désigne la fonction dérivée de B.
3. a. À l’aide des résultats de la partie 1, donner les variations de la fonction B sur l’intervalle [1;4].
b. En déduire la quantité de jus de fruits, au litre près, que l’entreprise doit vendre afin de réaliser un bénéfice maximal.