logo

TC. Problème n°4

Exercice n°1 : 15 mars 2021 Sujet 1

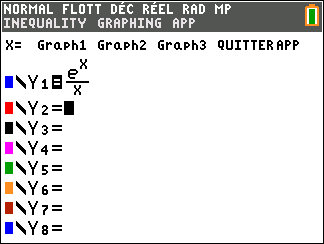
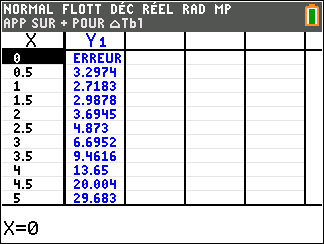
Soit f la fonction définie sur l’intervalle ]0;+\infty[ par : f(x)=\frac{e^x}{x}
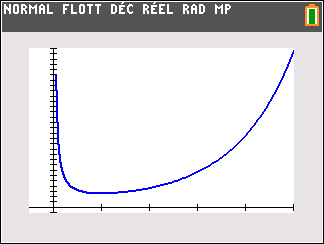
On note C_f la courbe représentative de la fonction f dans un repère orthonormé.
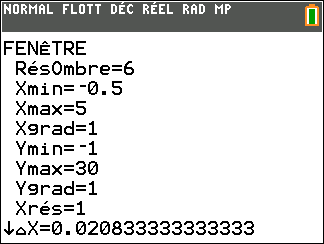
Avant de commencer l’exercice, il est bon de programmer sa TI 83 Premium CE.

je programme ma calculatrice

Au cours de l’exercice, on peut aussi utiliser la fenêtre active Géogébra ci-dessous pour conjecturer ou valider. Elle est composée de trois colonnes : la colonne à gauche est la colonne Algèbre, celle de milieu permet de faire du calcul formel ( calcul de dérivée, développer, factoriser, résoudre,…) et celle de droite correspond au graphique.

©2020 – Math’O karé SAS

Au clavier

A l’écran

Taper sur la touche f(x) en haut à gauche du clavier de la calculatrice.

En général le mode fonction est activé par défaut.

Si ce n’est pas le cas, taper sur la touche mode et sélectionner FONCTION sur la 5ème ligne. Puis quitter avec 2nde mode

On programme la fonction en complétant la ligne Y1= . Pour saisir x taper au clavier sur la touche X,T,O,n.

Pour afficher la table de valeurs, taper sur la touche 2nde et sur la touche graphe, le tableur apparaît. On peut modifier les paramètres du tableur, pour cela faire 2nde puis fenêtre et effectuer les modifications souhaitées, par exemple Début Tbl=0, Tbl=0.5,  AUTO et AUTO.

Remarque : on voit bien que 0 n’a pas d’image.

Compte-tenu du tableau obtenu précédemment, on modifie l’affichage du graphique en tapant sur la touche fenêtre et en modifiant les valeurs déjà présentes.

Voici par exemple, un paramétrage possible.

Taper sur la touche graphe, la représentation graphique de la fonction apparaît.

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.