TC. Problème n°5

Niveau terminale maths complémentaires, Thème d'étude : modèle défini par une fonction d'une variable

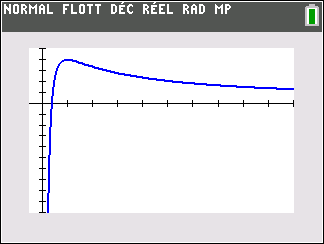
Dans le plan muni d’un repère, on considère ci-dessous la courbe $C_f$ représentative d’une
fonction $f$ , deux fois dérivable sur l’intervalle $]0;+\infty[$ .
La courbe $C_f$ admet une tangente horizontale $T$ au point $A(1;4)$ .

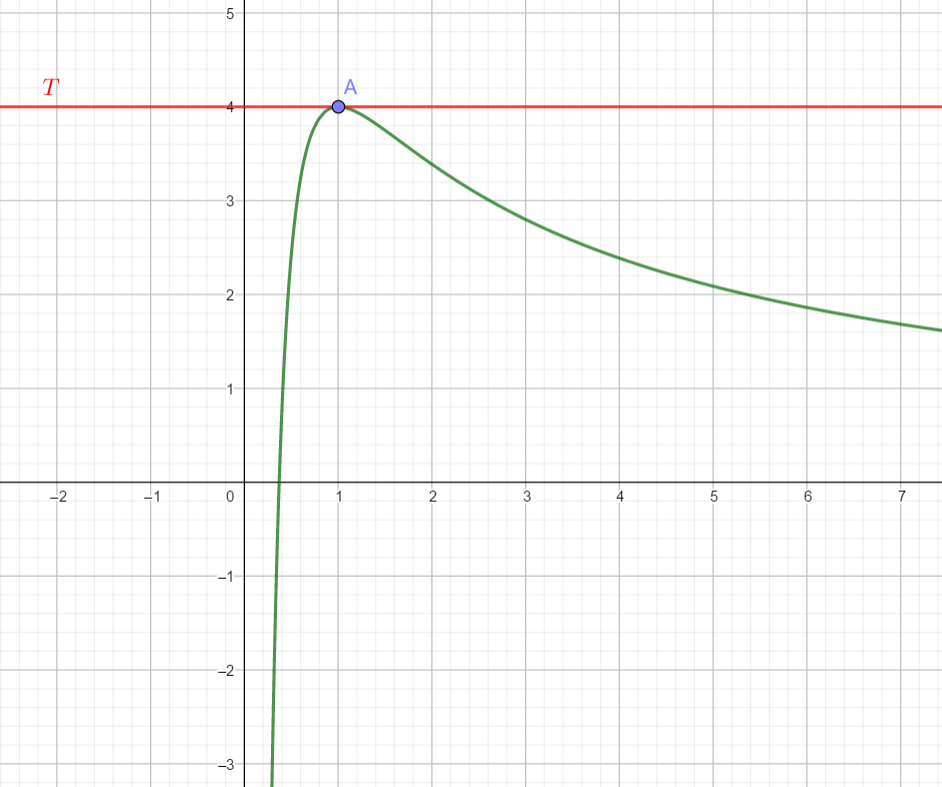
1. Préciser les valeurs $f(1)$ et $f'(1)$ .

On admet que la fonction $f$ est définie pour tout réel $x$ de l’intervalle $]0;+\infty[$ par :

$f(x)=\frac{a+bln(x)}{x}$

où $a$ et $b$ sont deux nombres réels.

2. Démontrer que, pour tout réel x strictement positif, on a :

$f'(x)=\frac{b-a-bln(x)}{x^2}$

3. En déduire les valeurs des réels $a$ et $b$ .

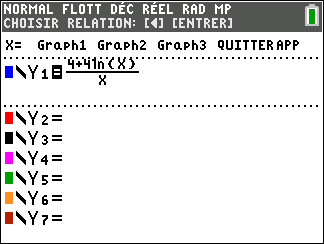
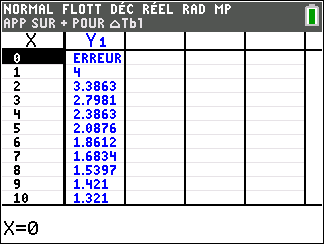
Dans la suite de l’exercice, on admet que la fonction $f$ est définie sur l’intervalle $]0;+\infty[$ par : $f(x)=\frac{4+4ln(x)}{x}$

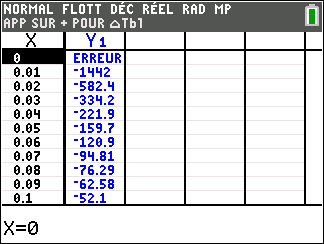
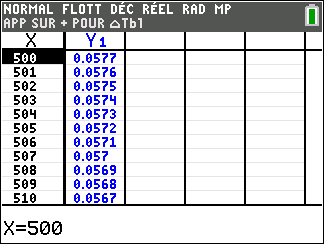
Avant de poursuivre l’exercice, il est bon de programmer sa TI 83 Premium CE.

4. Déterminer les limites de la fonction $f$ en $0^{+}$ et en $+\infty$ .

5. Déterminer le tableau de variations de $f$ sur l’intervalle $]0;+\infty[$ .

6. Démontrer que, pour tout réel x strictement positif, on a :

$f"(x)=\frac{-4+8ln(x)}{x^3}$ .

7. Montrer que la courbe $C_f$ possède un unique point d’inflexion $B$ dont on précisera les coordonnées.