logo

TC. Problème n°6

Cet exercice est composé de deux parties.
Certains résultats de la première partie seront utilisés dans la deuxième.
Partie 1 : Étude d’une fonction auxiliaire
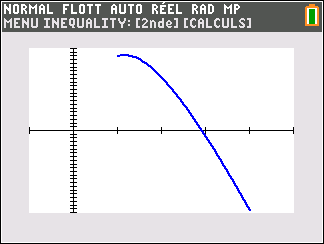
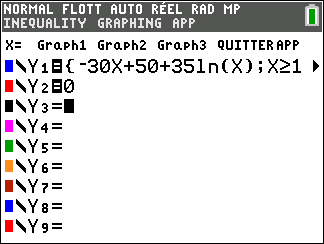
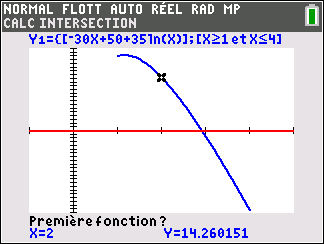
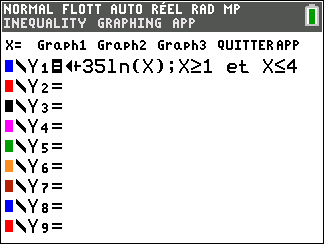
Soit la fonction f définie sur l’intervalle [1;4] par :
f(x)=-30x+50+35ln(x)

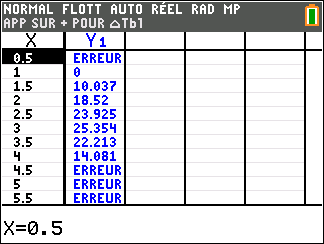
Avant de commencer l’exercice, il est bon de programmer sa TI 83 Premium CE.

je programme ma calculatrice

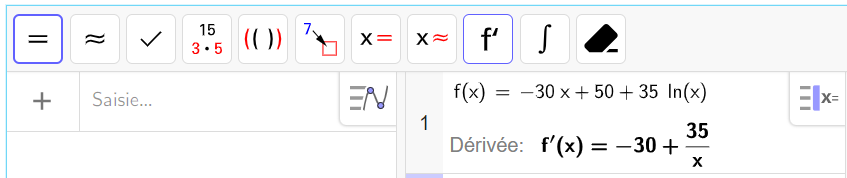
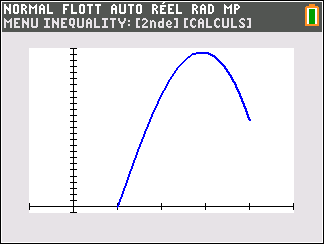
Au cours de l’exercice, on peut aussi utiliser la fenêtre active Géogébra ci-dessous pour conjecturer ou valider. Elle est composée de trois colonnes : la colonne à gauche est la colonne Algèbre, celle de milieu permet de faire du calcul formel ( calcul de dérivée, développer, factoriser, résoudre,…) et celle de droite correspond au graphique. A vous de saisir les fonctions dans la colonne de gauche.

1. On rappelle que f’ désigne la fonction dérivée de la fonction f.
a. Pour tout nombre réel x de l’intervalle [1;4], montrer que :
f'(x)=\frac{35-30x}{x}.

correction

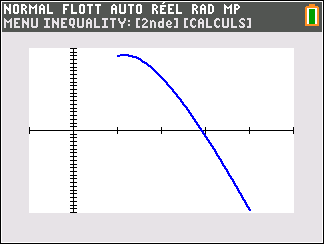
b. Déterminer le signe de f'(x) sur l’intervalle [1;4].

correction

c. En déduire le tableau de variations de f sur l’intervalle [1;4].

correction

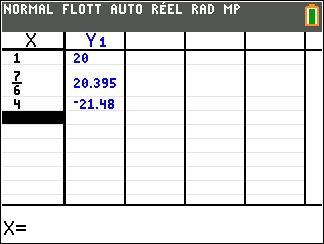
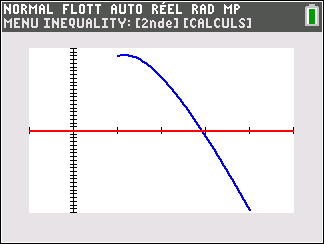
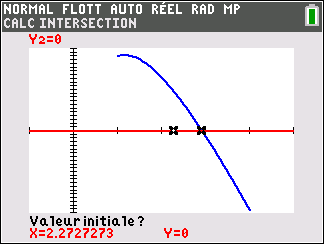
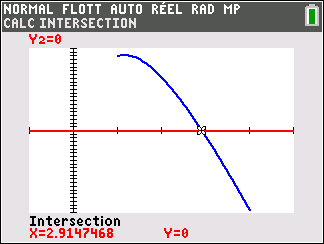
2. Justifier que l’équation f(x)=0 admet une unique solution, notée \alpha, sur l’intervalle [1;4] puis donner une valeur approchée de \alpha à 10^{-3} près.

correction
correction : encadrement de \alpha

3. Dresser le tableau de signe de f(x) sur [1;4].

correction

Partie 2 : Optimisation

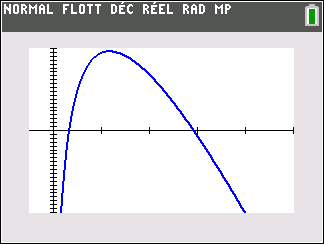
Une entreprise vend du jus de fruits. Pour x milliers de litres vendus, avec x appartenant à l’intervalle [1;4], l’analyse des ventes conduit à modéliser le bénéfice B(x) par l’expression donnée en milliers d’euros par :
B(x)=-15x^2+15x+35xln(x)

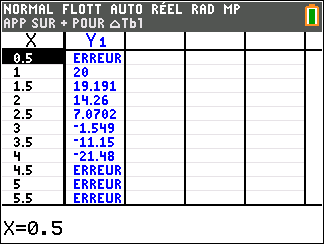
Avant de commencer l’exercice, il est bon de programmer sa TI 83 Premium CE.A

je programme ma calculatrice

1. D’après le modèle, calculer le bénéfice réalisé par l’entreprise lorsqu’elle vend 2500 litres de jus de fruits.
On donnera une valeur approchée à l’euro près de ce bénéfice.

correction

2. Pour tout x de l’intervalle [1;4], montrer que B'(x)=f(x) où B’ désigne la fonction dérivée de B.

correction

3. a. À l’aide des résultats de la partie 1, donner les variations de la fonction B sur l’intervalle [1;4].

correction

b. En déduire la quantité de jus de fruits, au litre près, que l’entreprise doit vendre afin de réaliser un bénéfice maximal.

correction

©2020 – Math’O karé SAS

Au clavier

A l’écran

Taper sur la touche f(x) en haut à gauche du clavier de la calculatrice.

En général le mode fonction est activé par défaut.

Si ce n’est pas le cas, taper sur la touche mode et sélectionner FONCTION sur la 5ème ligne. Puis quitter avec 2nde mode

Attention : la fonction est définie sur [1;4]

On tape sur la touche math et on sélectionne la ligne B par morceaux dans le menu déroulant. On valide par la touche entrer et on saisit la valeur 1 pour le nombre de morceaux.

On sélectionne OK et on valide par entrer. Dans le premier cadre on saisit -30X+50+35\times ln(X) pour atteindre le cadre suivant, on utilise la flèche du clavier et on y saisit  X\geq1 et X\leq 4.

Pour saisir \leq ou \geq appuyer sur la touche 2nde puis la touche test , rester dans la colonne TEST et sélectionner la ligne 6 ou la ligne 4.

Pour saisir et appuyer sur la touche 2nde puis la touche test, se positionner dans la colonne LOGIQ et sélectionner la ligne 1.

Pour afficher la table de valeurs, taper sur la touche 2nde et sur la touche graphe, le tableur apparaît. On peut modifier les paramètres du tableur, pour cela faire 2nde puis fenêtre et effectuer les modifications souhaitées, par exemple Début Tbl=0.5, Tbl=0.5,  AUTO et AUTO.

Remarque : on voit bien que seuls les nombres de  [1;4] ont une image.

Compte-tenu du tableau obtenu précédemment, on modifie l’affichage du graphique en tapant sur la touche fenêtre et en modifiant les valeurs déjà présentes.

Voici par exemple, un paramétrage possible.

Taper sur la touche graphe, la représentation graphique de la fonction apparaît.

f(x)=-30x+50+35ln(x) sur [1;4].

On veut montrer que pour tout nombre réel x , f'(x)=\frac{35-30x}{x}.

Ici le résultat du calcul de la dérivée est donné dans la question. Si cela n’avait pas été le cas, on peut conjecturer le résultat à l’aide de la fenêtre Géogébra donnée au début de l’exo. Pour cela saisir f(x)= (x+2)e^{-x} dans la colonne Calcul Formel ( celle du milieu) et cliquer sur l’onglet f’. La forme est bizarre mais comme ln(e)=1 ce sera la même que celle qu’obtient à la fin de la correction.

f(x)=-30x+50+35ln(x) sur [1;4].

1.On veut calculer f'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est la somme de deux fonctions u + v avec  u(x)=-30x+50 et v(x)=35ln(x).

On va utiliser la ligne n°1 du tableau n°1 ci-dessous.

Dérivées et opérations

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

Dérivées et fonctions composées

FonctionDérivée
v\circ u (v’\circ u)\times u’
u^2 2u’u
u^3 3u’u^2
u^n nu’u^{n-1}
\frac{1}{u} -\frac{u’}{u^2}
\sqrt{u} \frac{u’}{2\sqrt{u}}
cos(u) -u’sin(u)
sin(u) u’cos(u)
e^{u} u’e^{u}
ln(u) \frac{u’}{u}
\frac{1}{u^{n}} -\frac{nu’}{u^{n+1}}

2a.on veut calculer la dérivée  u'(x)

u(x)=-30x+50 est une  somme, on utilise la 1ère ligne du tableau « Dérivées et opérations ». 

u'(x)=(-30x+50)’

u'(x)=(-30x)’+50′

u'(x)=-30(x)’+0

u'(x)=-30\times 1

u'(x)=-30

2b.on veut calculer la dérivée  v'(x)

v(x)=35ln(x) est le produit d’une constante par une  fonction, on utilise la 2nde ligne du tableau « Dérivées et opérations ». 

v'(x)=(35ln(x))’

v'(x)=35(ln(x))’

On utilise la dernière ligne du tableau « Dérivées des fonctions de référence »

v'(x)=35\times \frac{1}{x]

v'(x)=\frac{35}{x}

Dérivées des fonctions de référence

 
Fonctionf(x)Dérivable sur f'(x)
constantef(x)=k\mathbf{R}f'(x)=0
identitéf(x)=x\mathbf{R}f'(x)=1
carréf(x)=x^2\mathbf{R}f'(x)=2x
cubef(x)=x^3\mathbf{R}f'(x)=3x^2
puissance nf(x)=x^n\mathbf{R}f'(x)=nx^{n-1}
inversef(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}
racine carréef(x)=\sqrt{x}]0;+\infty[ f'(x)=\frac{1}{2\sqrt{x}}
exponentiellef(x)=e^x\mathbf{R}f'(x)=e^x
sinusf(x)=sin(x)\mathbf{R}f'(x)=cos(x)
cosinusf(x)=cos(x)\mathbf{R}f'(x)=-sin(x)
logarithme népérienf(x)=ln(x)]0;+\infty[ f'(x)=\frac{1}{x}

3. On calcule la dérivée f'(x) 

On remplace  u’ par  -30 et v’ par \frac{35}{x} dans la formule u’+ v’ 

Voilà ce qu’il faut écrire sur votre copie :

f'(x)= (-30x+50+35ln(x))’\\f'(x)=(-30x+50)’+(35ln(x))’\\f'(x)=-30+\frac{35}{x}

On met au même dénominateur, ici x 

f'(x)=-30\times \frac{x}{x} +\frac{35}{x}\\f'(x)=- \frac{30x}{x} +\frac{35}{x}\\f'(x)= \frac{-30x+35}{x}

 

Il faut étudier le signe de f'(x)=\frac{35-30x}{x} sur [1;4]

x est positif, donc f'(x) est du signe de 35-30x.

On utilise la deuxième ligne du tableau ci-dessous, cliquer sur + la quantité est de la forme ax+b.

  1. de nombres positifs alors la quantité est positive.
  2. de nombres négatifs alors la quantité est négative.
  3. de nombres de signes contraires ou indéterminés alors on ne peut pas conclure

On peut factoriser et étudier le signe d’un produit

On peut résoudre la quantité >0 

…

On utilise le tableau suivant :

On utilise le résultat du cours suivant :

si \Delta>0

si \Delta=0

si \Delta<0

La quantité est toujours positive.

Exemples : les quantités x^2 , (2x+5)^4 sont toujours positives

La quantité est du signe de ce qui est élevé à la puissance.

Exemple : la quantité x^3 est du signe de x, la quantité (2x-1)^5 est du signe de 2x-1.

On fait un tableau de signes comme en seconde.

On étudie le signe du numérateur et le signe du dénominateur. Si nécessaire, ensuite on fait un tableau de signes comme en seconde.

On calcule la dérivée, on étudie son signe et on fait le tableau de variations. Ensuite, sur la dernière ligne du tableau de variations, on lit le signe de la quantité.  

On a a=-30, b=35, -\frac{b}{a}=-\frac{35}{(-30)}=\frac{7}{6} et le signe de a est négatif.

Voici le tableau de signes de  35-30x sur [1;4]

Comme f'(x) est du signe de 35-30x, f'(x) est positif sur l’intervalle [1;\frac{7}{6}]  et f'(x) est négatif sur l’intervalle [\frac{7}{6};4]  .

 

 

 

 

On veut déterminer les variations de la fonction f sur l’intervalle [1;4].
Utilisons la courbe de la calculatrice pour conjecturer les variations de f.

Il semble que la fonction f soit croissante puis  décroissante ensuite.

On a étudié le signe de f'(x) dans la question précédente : f'(x) est positif sur l’intervalle [1;\frac{7}{6}]  et f'(x) est négatif sur l’intervalle [\frac{7}{6};4]  .

On peut paramétrer la tableur de la calculatrice en mode demande pour déterminer les images de 1, \frac{7}{6}  et de 4 .

Puis on dresse le tableau de variations de f sur [1;4]. 

 

 

 

On va justifier que l’équation f(x)=0 admet une unique solution, notée \alpha, sur l’intervalle [1;4] puis donner une valeur approchée de \alpha à 10^{-3} près.

On peut conjecturer la réponse avec la courbe de la calculatrice.

La courbe coupe l’axe des abscisses entre  2 et 3

On visualise ensuite le phénomène sur le tableau de variations.

Sur l’intervalle [1;\frac{7}{6}], le minimum est  20 donc l’équation f(x)=0 n’y admet pas de solution .

Sur l’intervalle [\frac{7}{6};4] la fonction f est  continue et  strictement décroissante.

Comme  0\in]-21.5;20.4[ alors l’équation f(x)=0 admet une unique solution notée \alpha sur l’intervalle [\frac{7}{6};4].

Au clavier

A l’écran

Taper sur la touche f(x) en haut à gauche du clavier de la calculatrice.

En général le mode fonction est activé par défaut.

Si ce n’est pas le cas, taper sur la touche mode et sélectionner FONCTION sur la 5ème ligne. Puis quitter avec 2nde mode

On programme la fonction en complétant la ligne Y1= . Pour saisir x taper au clavier sur la touche X,T,O,n.

Puis taper Y2=0

 

Taper sur la touche  graphe

Taper sur la touche 2nde et la touche trace puis sélectionner 5:intersection dans le menu. Appuyer sur entrer.

 

La première fonction est bien le Y1 qui s’affiche en haut, on valide par entrer. L’écran suivant qui s’affiche correspond à Y2, on valide encore par entrer. Le nouvel écran demande la valeur initiale, avec les flèches du clavier on se positionne à gauche du point d’intersection. 

On fait entrer et on peut lire en bas de l’écran les coordonnées du point d’intersection.

Il ne reste plus qu’à donner un encadrement de \alpha à 10^{-3} près.

2.914\leq \alpha \leq 2.915.

 

 

En lisant le tableau de variations suivant

On peut en déduire  le tableau de signe de  f

Au clavier

A l’écran

Taper sur la touche f(x) en haut à gauche du clavier de la calculatrice.

En général le mode fonction est activé par défaut.

Si ce n’est pas le cas, taper sur la touche mode et sélectionner FONCTION sur la 5ème ligne. Puis quitter avec 2nde mode

Attention : la fonction est définie sur [1;4]

On tape sur la touche math et on sélectionne la ligne B par morceaux dans le menu déroulant. On valide par la touche entrer et on saisit la valeur 1 pour le nombre de morceaux.

On sélectionne OK et on valide par entrer. Dans le premier cadre on saisit -15X^2+15X+35X\times ln(X) pour atteindre le cadre suivant, on utilise la flèche du clavier et on y saisit  X\geq1 et X\leq 4.

Pour saisir \leq ou \geq appuyer sur la touche 2nde puis la touche test , rester dans la colonne TEST et sélectionner la ligne 6 ou la ligne 4.

Pour saisir et appuyer sur la touche 2nde puis la touche test, se positionner dans la colonne LOGIQ et sélectionner la ligne 1.

 

Pour afficher la table de valeurs, taper sur la touche 2nde et sur la touche graphe, le tableur apparaît. On peut modifier les paramètres du tableur, pour cela faire 2nde puis fenêtre et effectuer les modifications souhaitées, par exemple Début Tbl=0.5, Tbl=0.5,  AUTO et AUTO.

Remarque : on voit bien que seuls les nombres de  [1;4] ont une image.

Compte-tenu du tableau obtenu précédemment, on modifie l’affichage du graphique en tapant sur la touche fenêtre et en modifiant les valeurs déjà présentes.

Voici par exemple, un paramétrage possible.

Taper sur la touche graphe, la représentation graphique de la fonction apparaît.

2500 litres de jus de fruits représentent 2,5 milliers de litres de jus de fruits.

Pour calculer le bénéfice réalisé par l’entreprise lorsqu’elle vend 2500 litres de jus de fruits, on remplace x par 2,5 dans B(x)=-15x^2+15x+35xln(x).

B(2.5)=-15\times 2.5^2+15\times 2.5+35\times 2.5\times ln(2.5)\\B(2.5)=23.925

Le bénéfice est de 23.925 milliers d’euros, soit  23925 euros.

B(x)=-15x^2+15x+35xln(x) sur [1;4].

On veut montrer que pour tout nombre réel x , B'(x)=f(x).

Ici le résultat du calcul de la dérivée est donné dans la question. Si cela n’avait pas été le cas, on peut conjecturer le résultat à l’aide de la fenêtre Géogébra donnée au début de l’exo. Pour cela saisir B(x)=-15x^2+15x+35xln(x) dans la colonne Calcul Formel ( celle du milieu) et cliquer sur l’onglet f’. 

B(x)=-15x^2+15x+35xln(x)

1.On veut calculer B'(x).

On répond à la question suivante : f(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est la somme de deux fonctions u + v avec  u(x)=-15x^2+15x et v(x)=35xln(x).

On va utiliser la ligne n°1 du tableau n°1 ci-dessous.

Dérivées et opérations

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

Dérivées et fonctions composées

FonctionDérivée
v\circ u (v’\circ u)\times u’
u^2 2u’u
u^3 3u’u^2
u^n nu’u^{n-1}
\frac{1}{u} -\frac{u’}{u^2}
\sqrt{u} \frac{u’}{2\sqrt{u}}
cos(u) -u’sin(u)
sin(u) u’cos(u)
e^{u} u’e^{u}
ln(u) \frac{u’}{u}
\frac{1}{u^{n}} -\frac{nu’}{u^{n+1}}

2a.on veut calculer la dérivée  u'(x)

u(x)=-15x^2+15x est une  somme, on utilise la 1ère ligne du tableau « Dérivées et opérations ». 

u'(x)=(-15x^2+15x)’

u'(x)=(-15x^2)’+(15x)’

u'(x)=-15(x^2)’+15(x)’

u'(x)=-15\times 2x+15\times 1

u'(x)=-30x+15

2b.on veut calculer la dérivée  v'(x)

v(x)=35xln(x) est le produit de deux fonctions, on utilise la 3ième ligne du tableau « Dérivées et opérations ». 

v'(x)=(35x)’\times ln(x)+35x\times (ln(x))’

v'(x)=35ln(x)+35x\times \frac{1}{x}

v'(x)=35ln(x)+35

Dérivées des fonctions de référence

 
Fonctionf(x)Dérivable sur f'(x)
constantef(x)=k\mathbf{R}f'(x)=0
identitéf(x)=x\mathbf{R}f'(x)=1
carréf(x)=x^2\mathbf{R}f'(x)=2x
cubef(x)=x^3\mathbf{R}f'(x)=3x^2
puissance nf(x)=x^n\mathbf{R}f'(x)=nx^{n-1}
inversef(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}
racine carréef(x)=\sqrt{x}]0;+\infty[ f'(x)=\frac{1}{2\sqrt{x}}
exponentiellef(x)=e^x\mathbf{R}f'(x)=e^x
sinusf(x)=sin(x)\mathbf{R}f'(x)=cos(x)
cosinusf(x)=cos(x)\mathbf{R}f'(x)=-sin(x)
logarithme népérienf(x)=ln(x)]0;+\infty[ f'(x)=\frac{1}{x}

3. On calcule la dérivée f'(x) 

On remplace  u’ par  -30x+15 et v’ par 35ln(x)+35 dans la formule u’+ v’ 

Voilà ce qu’il faut écrire sur votre copie :

B'(x)=(-15x^2+15x+35xln(x))’\\\hspace{0.9cm}=-30x+15+(35xln(x))’\\\hspace{0.9cm}=-30x+15+(35x)’\times ln(x)+35x\times (ln(x))’\\\hspace{0.9cm}=-30x+15+35ln(x)+35x\times \frac{1}{x}\\\hspace{0.9cm}=-30x+15+35ln(x)+35\\\hspace{0.9cm}=-30x+50+35ln(x)\\\hspace{0.9cm}=f(x)

 

 

Comme B'(x)=f(x), on va utiliser le tableau de signes de f pour en déduire les variations de B.

Voici le tableau de variations de  B sur [1;4].

D’après le tableau de variations de  B sur [1;4].

Le maximum est B(\alpha).

On remplace \alpha par 2.914 dans B(x)=-15x^2+15x+35xln(x).

B(2.914)=-15\times 2.914^2+15\times 2.914+35\times 2.914 \times ln(2.914)

B(2.914)=25.42

Le maximum est 25.42 milliers d’euros, soit 25420 euros.

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.