Sommaire
Au cours des exercices, on peut aussi utiliser la fenêtre active Géogébra ci-dessous pour conjecturer ou valider. Elle est composée de trois colonnes : la colonne à gauche est la colonne Algèbre, celle de milieu permet de faire du calcul formel ( calcul de dérivée, développer, factoriser, résoudre,…) et celle de droite correspond au graphique.
Exercice n°1 : Asie 7 juin 2021 Jour 1
Partie I
Soit l’équation différentielle y’=-0.4y+0.4 où y désigne une fonction de la variable t, définie et dérivable sur [0;+\infty[.
1. a. Déterminer une solution particulière constante de cette équation différentielle
b. En déduire l’ensemble des solutions de cette équation différentielle
c. Déterminer la fonction g, solution de cette équation différentielle, qui vérifie
g(0)=10.
Partie II
Soit p la fonction définie et dérivable sur l’intervalle [0;+\infty[ par
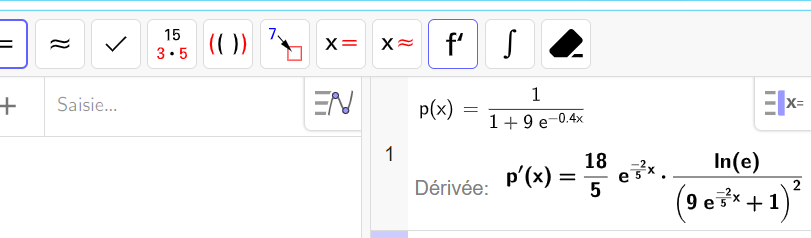
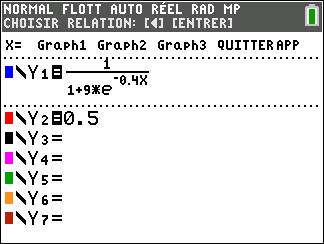
p(t)=\frac{1}{g(t)}=\frac{1}{1+9e^{-0.4t}}
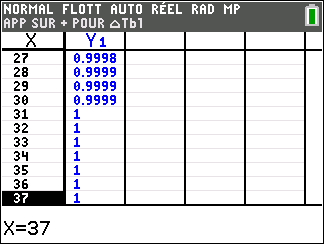
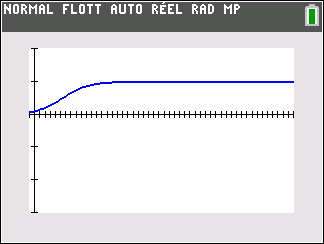
1. Déterminer la limite de p en +\infty.
2. Montrer que
p'(t)=\frac{3.6e^{-0.4t}}{(1+9e^{-0.4t})^2}
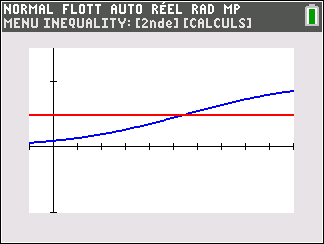
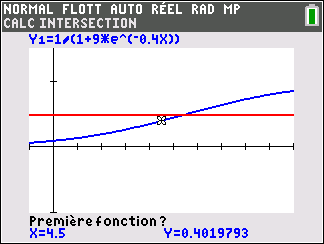
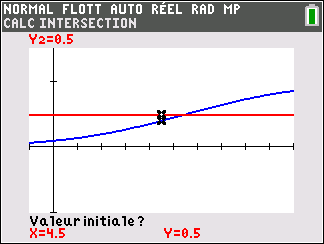
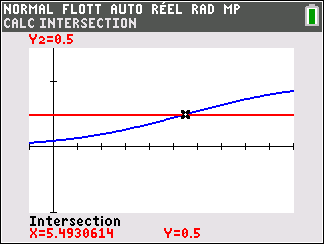
3. a. Montrer que l’équation p(t)=\frac{1}{2} admet une unique solution \alpha sur [0;+\infty[.
b. Déterminer une valeur approchée de \alpha à 10^{-1} près à l’aide d’une calculatrice.
Partie III
1. p désigne la fonction de la partie II.
Vérifier que p est solution de l’équation différentielle y’=0.4y(1-y)
avec la condition initiale y(0)=\frac{1}{10} où y désigne une fonction définie et dérivable sur [0;+\infty[.
2. Dans un pays en voie de développement, en l’année 2020, 10 % des écoles ont accès à internet.
Une politique volontariste d’équipement est mise en œuvre et on s’intéresse à l’évolution de la proportion des écoles ayant accès à internet.
On note t le temps écoulé, exprimé en année, depuis l’année 2020.
La proportion des écoles ayant accès à internet à l’instant t est modélisée par p(t).
Interpréter dans ce contexte la limite de la question II 1 puis la valeur approchée de \alpha
de la question II 3. b. ainsi que la valeur p(0).
Exercice n°2 : Métropole 8 Juin 2021 Exercice A
Partie 1
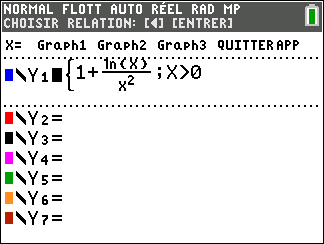
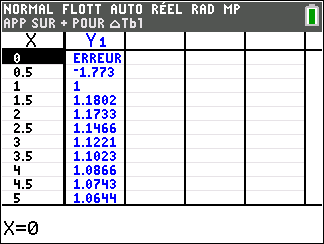
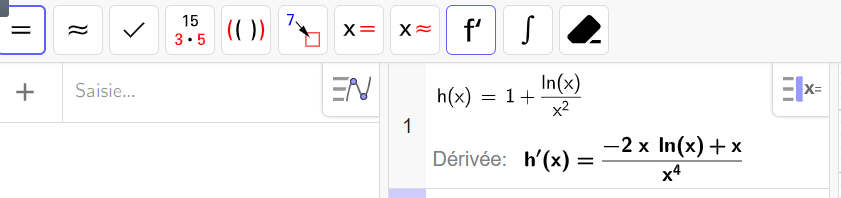
On désigne par h la fonction définie sur l’intervalle ]0;+\infty[ par :
h(x)=1+\frac{ln(x)}{x^2}
On admet que la fonction h est dérivable sur ]0;+\infty[ et on note h’ sa fonction dérivée.
Avant de commencer l’exercice, il est bon de programmer sa TI 83 Premium CE.
1. Déterminez les limites de h en 0 et en +\infty.
2. Montrer que, pour tout nombre réel x de ]0;+\infty[, h'(x)=\frac{1-2ln(x)}{x^3}.
3. En déduire le tableau de variations de la fonction h sur l’intervalle ]0;+\infty[.
4. Montrer que l’équation h(x)=0 admet une solution unique \alpha appartenant à ]0;+\infty[ et vérifier que : \frac{1}{2}<\alpha<1.
5. Déterminer le signe de h(x) pour x appartenant à ]0;+\infty[.
Partie 2
On désigne par f_1 et f_2 les fonctions définies sur ]0;+\infty[ par :
f_1(x)=x-1-\frac{ln(x)}{x^2} et f_2(x)=x-2-\frac{2ln(x)}{x^2}
On note C_1 et C_2 les représentations graphiques respectives de f_1 et f_2.
1. Montrer que, pour tout nombre réel x appartenant à ]0;+\infty[, on a :
f_1(x)-f_2(x)=h(x).
2. Déduire des résultats de la Partie 1 la position relative des courbes C_1 et C_2 .
On justifiera que leur unique point d’intersection a pour coordonnées (\alpha;\alpha).
On rappelle que \alpha est l’unique solution de l’équation h(x)=0.
Exercice n°3 : Baccalauréat Métropole 13 septembre 2021 J2
Partie I
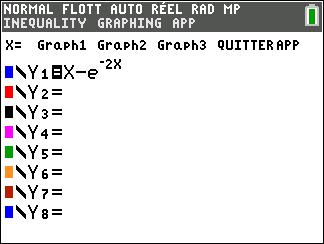
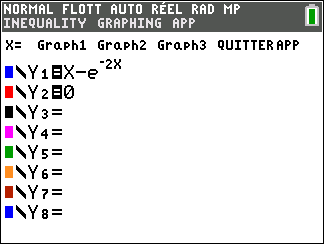
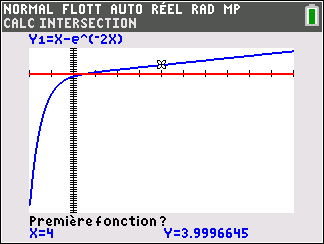
On considère la fonction f définie sur \mathbf{R} par f(x)=x-e^{-2x}
.
On appelle \Gamma la courbe représentative de la fonction f dans un repère orthonormé.
Avant de commencer l’exercice, il est bon de programmer sa TI 83 Premium CE.
1. Déterminer les limites de la fonction f en -\infty et en +\infty.
2. Étudier le sens de variation de la fonction f sur \mathbf{R} et dresser son tableau de variation.
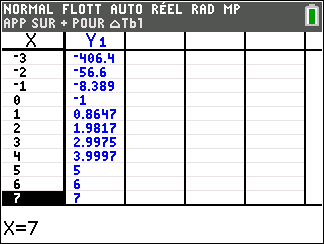
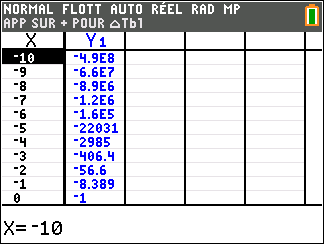
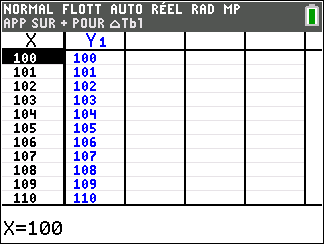
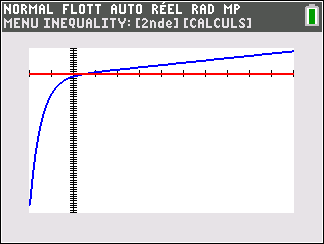
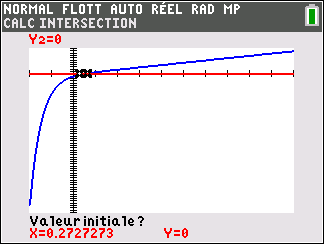
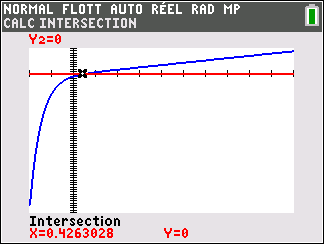
3. Montrer que l’équation f(x)=0 admet une unique solution \alpha sur \mathbf{R}, dont on donnera une valeur approchée à 10^{-2} près.
4. Déduire des questions précédentes le signe de f(x) suivant les valeurs de x.
Partie II
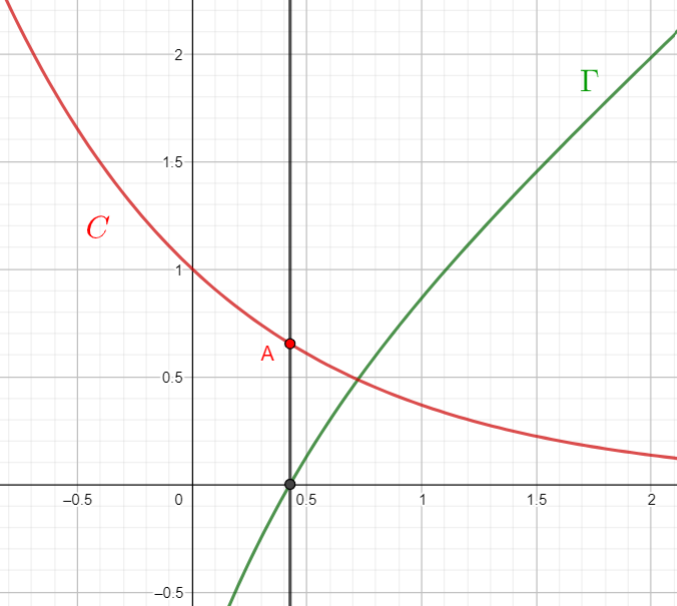
Dans le repère orthonormé , on appelle C la courbe représentative de la fonction g définie sur \mathbf{R} par :
g(x)=e^{-x}.
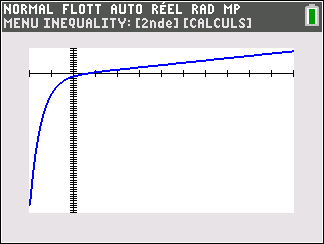
La courbe C et la courbe \Gamma (qui représente la fonction f de la Partie I) sont tracées sur le graphique donné en annexe qui est à compléter et à rendre avec la copie.
Le but de cette partie est de déterminer le point de la courbe C le plus proche de l’origine O du repère et d’étudier la tangente à C en ce point.
1. Pour tout nombre réel t, on note M le point de coordonnées (t;e^{-t}) de la courbe C .
On considère la fonction h qui, au nombre réel t, associe la distance OM.
On a donc : h(t)=OM, c’est-à-dire :
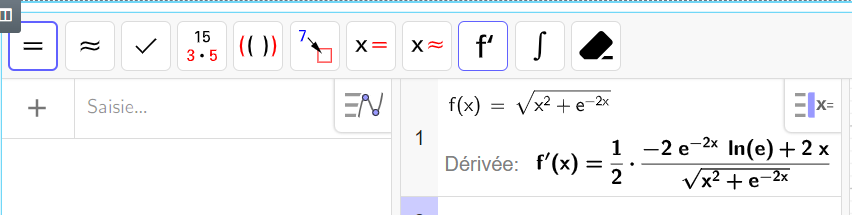
h(t)=\sqrt{t^2+e^{-2t}}
a. Montrer que, pour tout nombre réel t, h'(t)=\frac{f(t)}{\sqrt{t^2+e^{-2t}}} où f désigne la fonction étudiée dans la Partie I.
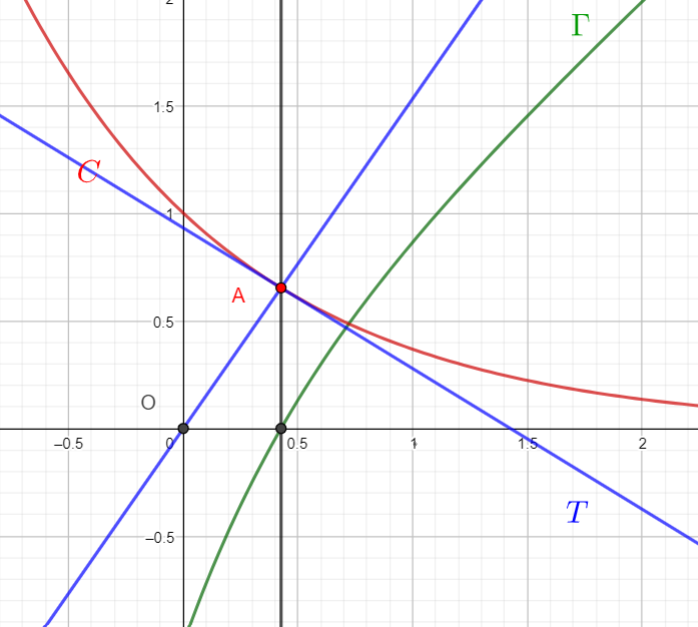
b. Démontrer que le point A de coordonnées (\alpha;e^{-\alpha}) est le point de la courbe C pour lequel la longueur OM est minimale.
Placer ce point sur le graphique donné en annexe, à rendre avec la copie.
2. On appelle T la tangente en A à la courbe C .
a. Exprimer en fonction de \alpha le coefficient directeur de la tangente T.
On rappelle que le coefficient directeur de la droite (OA) est égal à \frac{e^{-\alpha}}{\alpha}.
On rappelle également le résultat suivant qui pourra être utilisé sans démonstration :
Dans un repère orthonormé du plan, deux droites D et D’ de coefficients directeurs respectifs m et m’ sont perpendiculaires si, et seulement si le produit m.m’ est égal à -1.
b. Démontrer que la droite (OA)et la tangente T sont perpendiculaires.
Tracer ces droites sur le graphique donné en annexe, à rendre avec la copie.
Exercice n°4 : Centres étrangers 10 juin 2021 Exercice B
Partie A : Détermination d’une fonction f et résolution d’une équation différentielle
On considère la fonction f définie sur \mathbf{R} par :
f(x)=e^x+ax+be^{-x}
où a et b sont des nombres réels que l’on propose de déterminer dans cette partie.
Dans le plan muni d’un repère d’origine O, on a représenté ci-dessous la courbe C , représentant la fonction f, et la tangente (T) à la courbe C au point d’abscisse 0.
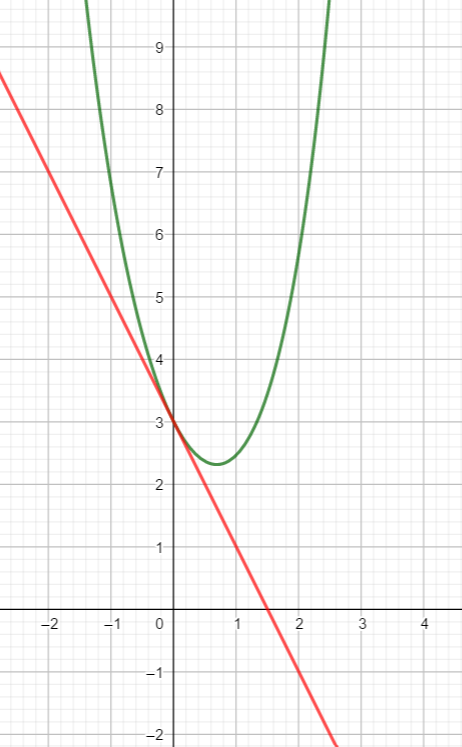
1. Par lecture graphique, donner les valeurs de f(0) et de f'(0).
2. En utilisant l’expression de la fonction f, exprimer f(0) en fonction de b et en déduire la valeur de b .
3. On admet que la fonction f est dérivable sur \mathbf{R} et on note f’ sa fonction dérivée.
a. Donner, pour tout réel x, l’expression de f'(x).
b. Exprimer f'(0) en fonction de a.
c. En utilisant les questions précédentes, déterminer a, puis en déduire l’expression de f(x).
4. On considère l’équation différentielle : (E) \hspace{0.5cm}y’+y=2e^x-x-1
a. Vérifier que la fonction g définie sur \mathbf{R} par : g(x)=e^x-x+2e^{-x} est solution de l’équation (E).
b. Résoudre l’équation différentielle y’+y=0.
c. En déduire toutes les solutions de l’équation (E).
Partie B : Étude de la fonction g sur [1;+\infty[
1. Vérifier que pour tout réel x, on a :
e^{2x}-e^{x}-2=(e^x-2)(e^x+1)
2. En déduire une expression factorisée de g'(x), pour tout réel x.
3. Étudier le sens de variation de la fonction g sur [1;+\infty[.
Exercice n°5 : Amérique du Nord mai 2021 Exercice A
Pour chacune des affirmations suivantes, indiquer si elle est vraie ou fausse.
On justifiera chaque réponse.
Affirmation 1 : Pour tous réels a et b, (e^{a+b})^2=e^{2a}+e^{2b}
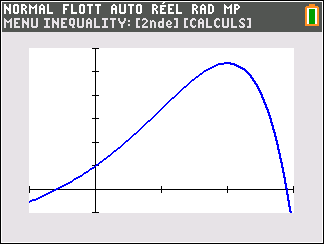
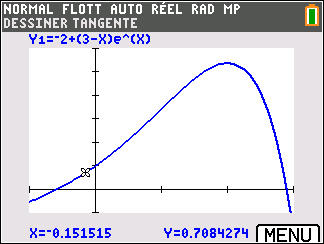
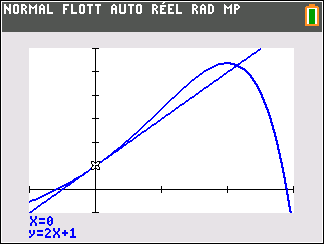
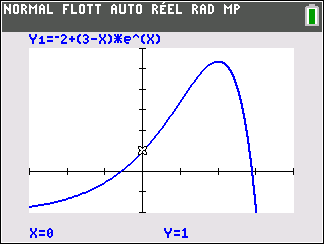
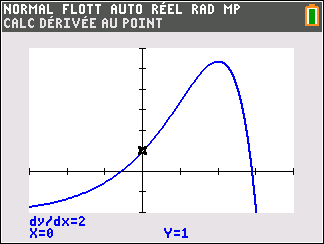
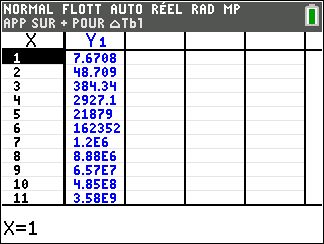
Affirmation 2 : Dans le plan muni d’un repère, la tangente au point A d’abscisse 0 à la courbe représentative de la fonction f définie sur \mathbf{R} par f(x)=-2+(3-x)e^x admet pour équation réduite y=2x+1 .
Affirmation 3 : lim_{x\to{+\infty}}\hspace{0.3cm}e^{2x}-e^x+\frac{3}{x}=0
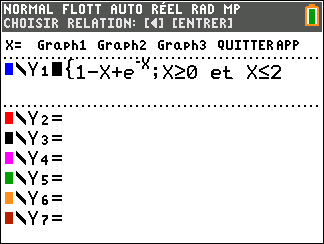
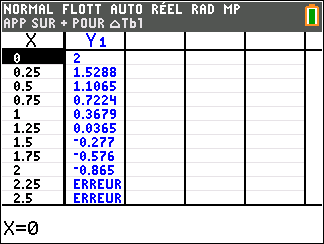
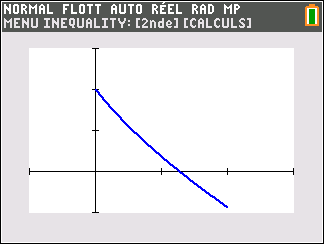
Affirmation 4 : L’équation 1-x+e^{-x}=0 admet une seule solution appartenant à l’intervalle
[0;2] .
Avant d’essayer de répondre, on peut conjecturer la réponse à l’aide de la calculatrice TI 83 Premium CE.
Affirmation 5 : La fonction gdéfinie sur \mathbf{R} par g(x)=x^2-5x+e^x est convexe.