Sommaire
Limites des fonctions de référence
La fonction carré
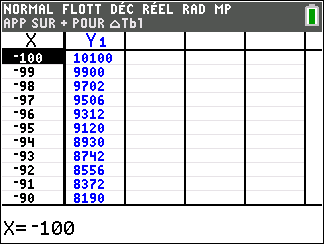
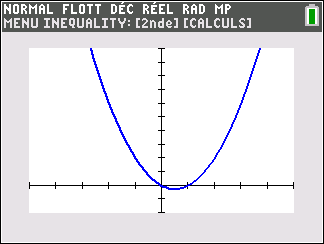
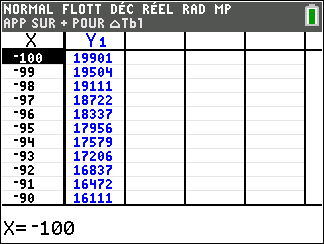
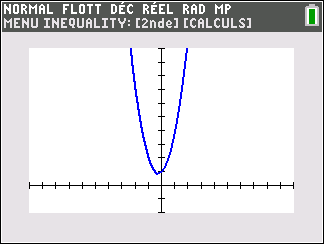
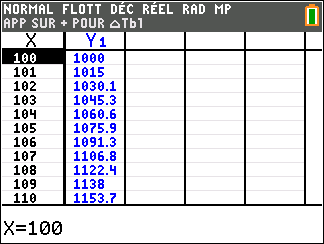
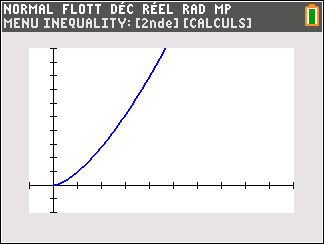
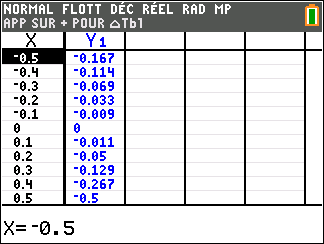
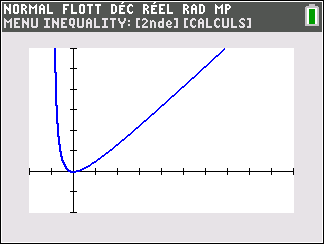
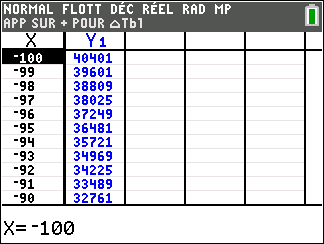
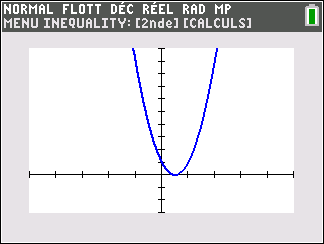
f(x)=x^2 définie sur \mathbf{R}.
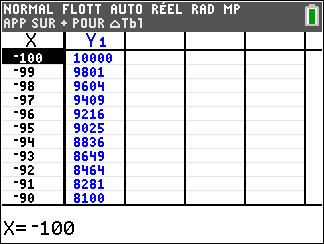
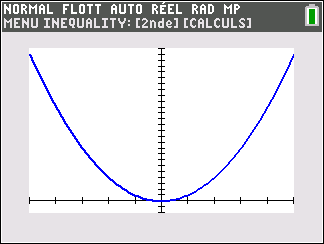
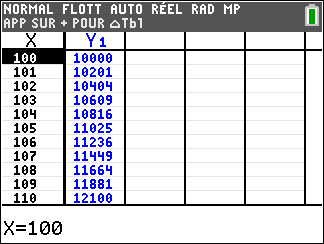
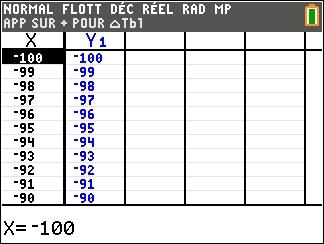
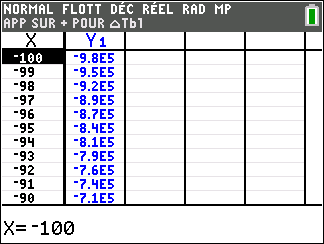
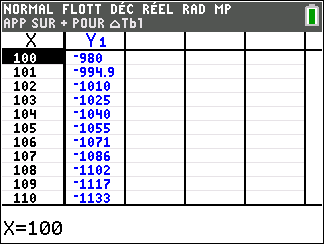
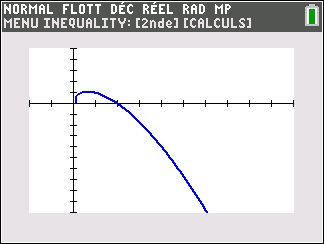
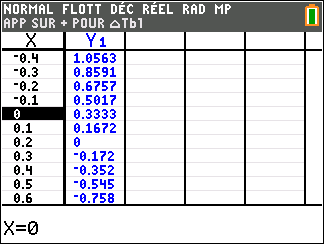
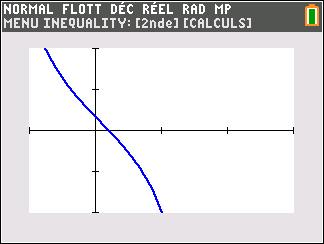
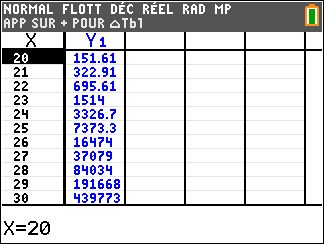
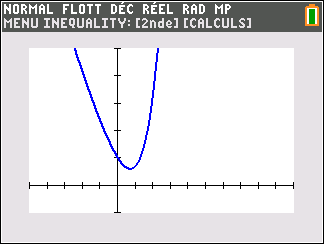
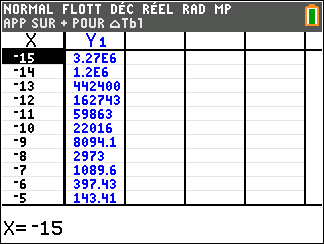
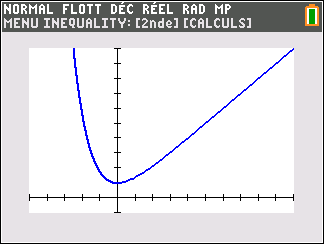
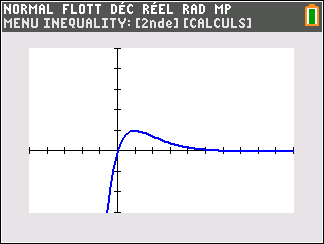
Lorsque les valeurs de x se rapprochent de -\infty, on peut voir dans le tableur de gauche en le lisant du bas vers le haut ou sur la partie de la courbe située à gauche que les valeurs de f(x) se rapprochent de +\infty.
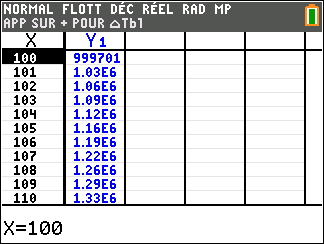
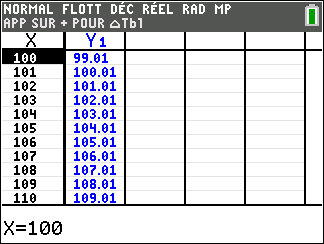
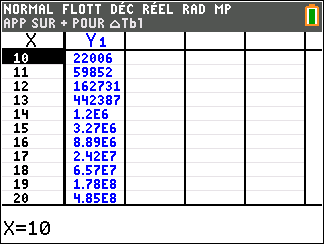
Lorsque les valeurs de x se rapprochent de +\infty, on peut voir dans le tableur de droite en le lisant du haut vers le bas ou sur la partie de la courbe située à droite que les valeurs de f(x) se rapprochent de +\infty.
A savoir :
lim_{x\to-\infty}\hspace{0.3cm}x^2=+\infty et lim_{x\to+\infty}\hspace{0.3cm}x^2=+\infty
La fonction identité
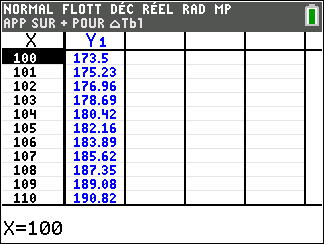
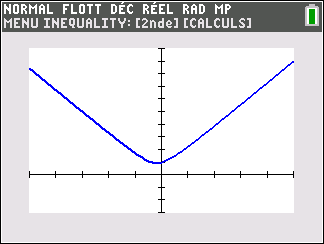
f(x)=x définie sur \mathbf{R}.
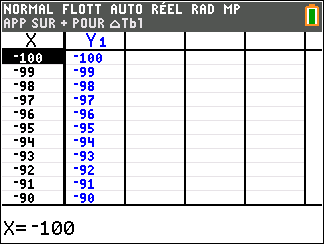
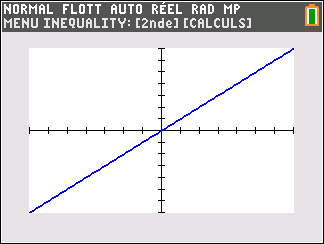
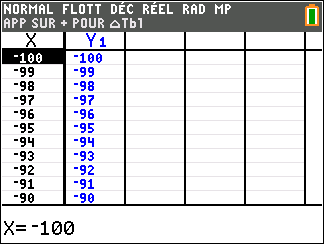
Lorsque les valeurs de x se rapprochent de -\infty, on peut voir dans le tableur de gauche en le lisant du bas vers le haut ou sur la partie de la courbe située à gauche que les valeurs de f(x) se rapprochent de -\infty.
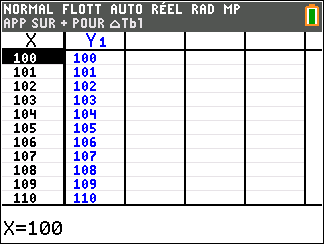
Lorsque les valeurs de x se rapprochent de +\infty, on peut voir dans le tableur de droite en le lisant du haut vers le bas ou sur la partie de la courbe située à droite que les valeurs de f(x) se rapprochent de +\infty.
A savoir :
lim_{x\to-\infty}\hspace{0.3cm}x=-\infty et lim_{x\to+\infty}\hspace{0.3cm}x=+\infty
La fonction constante
f(x)=k définie sur \mathbf{R}. Pour la manip avec la calculatrice, prenons par exemple k=3
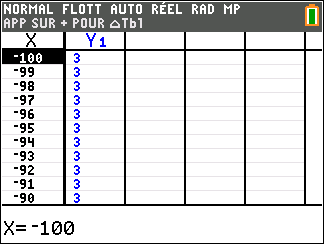
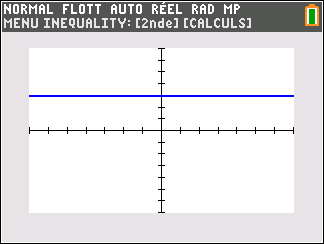
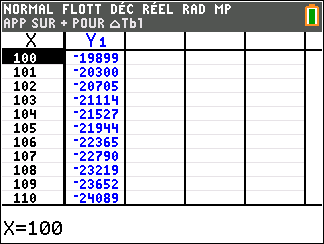
Lorsque les valeurs de x se rapprochent de -\infty, on peut voir dans le tableur de gauche en le lisant du bas vers le haut ou sur la partie de la courbe située à gauche que les valeurs de f(x) se rapprochent de 3.
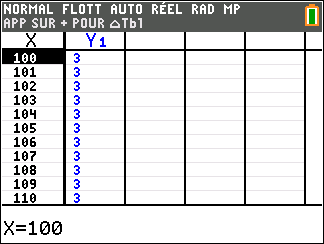
Lorsque les valeurs de x se rapprochent de +\infty, on peut voir dans le tableur de droite en le lisant du haut vers le bas ou sur la partie de la courbe située à droite que les valeurs de f(x) se rapprochent de 3.
Revenons au cas général
A savoir :
lim_{x\to-\infty}\hspace{0.3cm}k=k et lim_{x\to+\infty}\hspace{0.3cm}k=k
Remarque : ce n’est pas surprenant car constante signifie qui ne varie pas avec x.
La fonction inverse
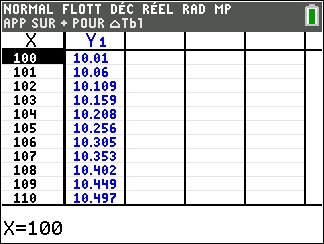
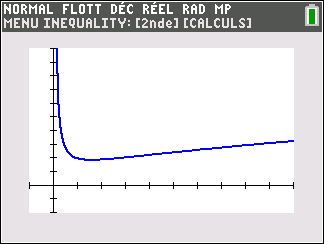
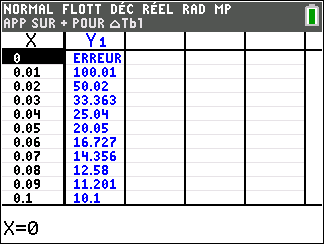
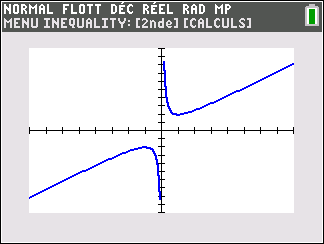
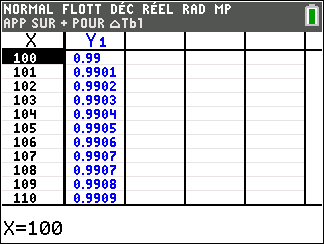
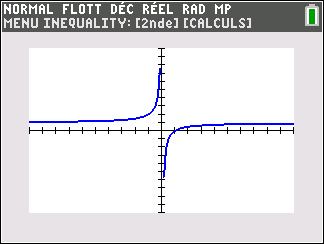
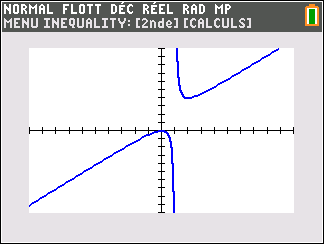
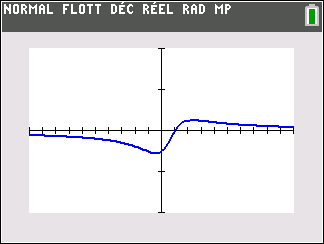
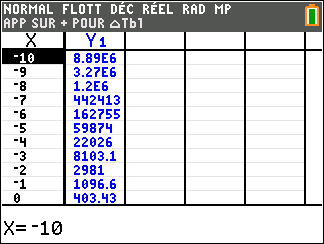
f(x)=\frac{1}{x} définie sur \mathbf{R}^{*}( c’est-à-dire l’ensemble des réels non nuls).
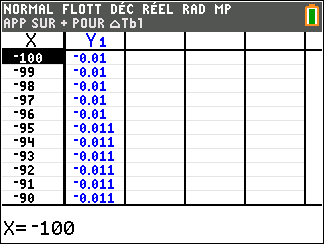
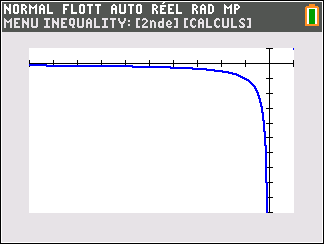
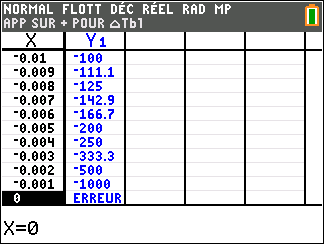
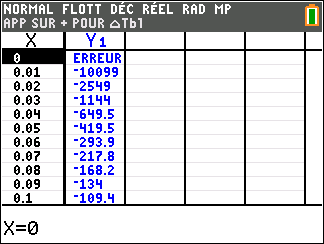
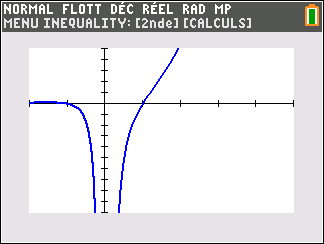
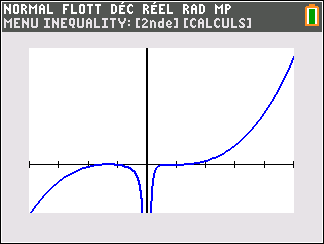
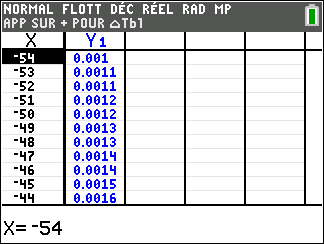
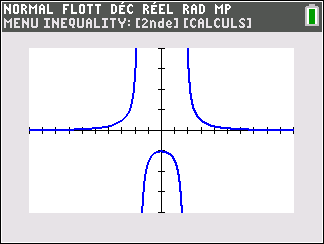
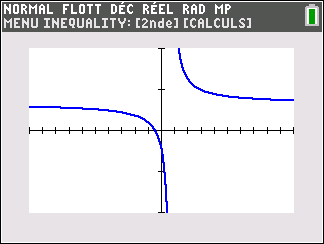
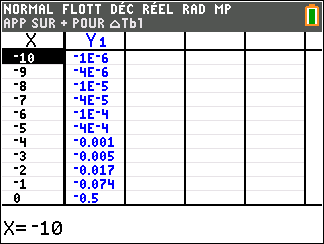
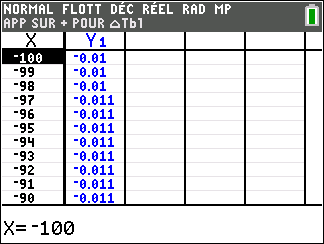
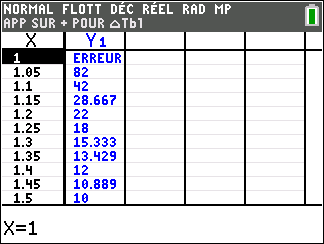
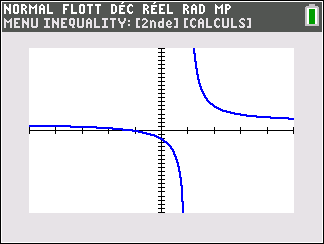
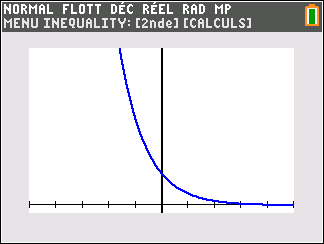
Lorsque les valeurs de x se rapprochent de -\infty, on peut voir dans le tableur de gauche en le lisant du bas vers le haut ou sur la partie de la courbe située à gauche que les valeurs de f(x) se rapprochent de 0.
Lorsque les valeurs de x se rapprochent de 0 par valeurs négatives, on peut voir dans le tableur de droite ou sur la partie de la courbe située à droite que les valeurs de f(x) se rapprochent de -\infty.
A savoir :
lim_{x\to-\infty}\hspace{0.3cm}\frac{1}{x}=0 et lim_{x\to 0^{-}}\hspace{0.3cm}\frac{1}{x}=-\infty
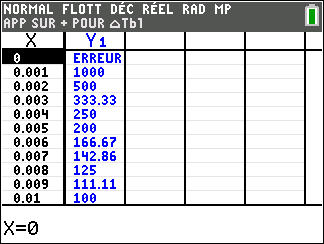
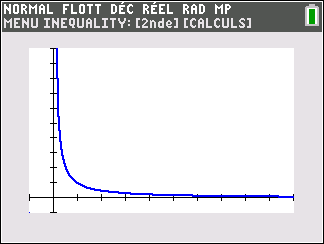
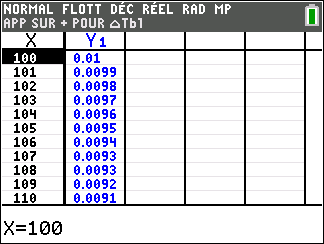
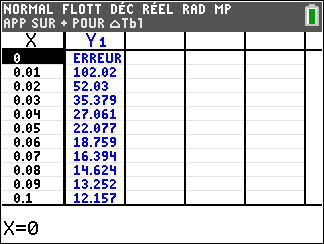
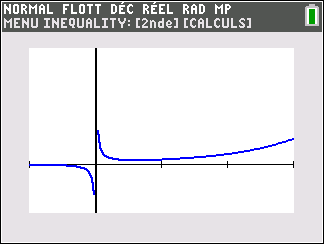
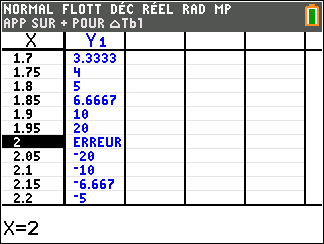
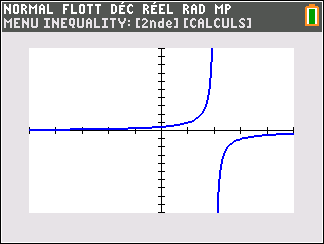
Lorsque les valeurs de x se rapprochent de 0 par valeurs positives, on peut voir dans le tableur de gauche en le lisant du bas vers le haut ou sur la partie de la courbe située à gauche que les valeurs de f(x) se rapprochent de +\infty.
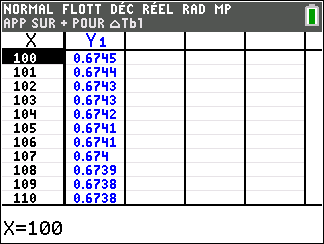
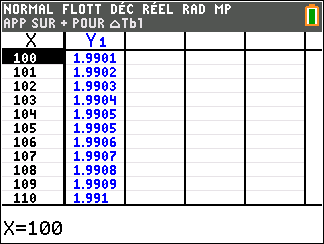
Lorsque les valeurs de x se rapprochent de +\infty, on peut voir dans le tableur de droite ou sur la partie de la courbe située à droite que les valeurs de f(x) se rapprochent de 0.
A savoir :
lim_{x\to 0^{+}}\hspace{0.3cm}\frac{1}{x}=+\infty et lim_{x\to +\infty}\hspace{0.3cm}\frac{1}{x}=0
La fonction racine carrée
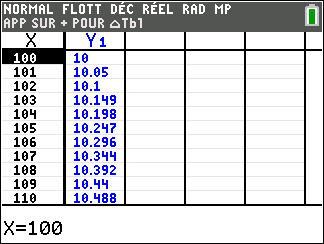
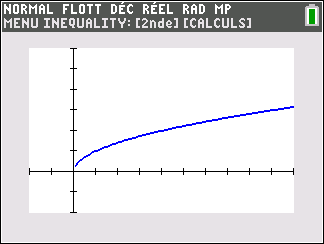
f(x)=\sqrt{x} définie sur [0;+\infty( c’est-à-dire l’ensemble des réels positifs ou nuls).
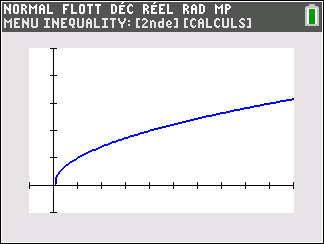
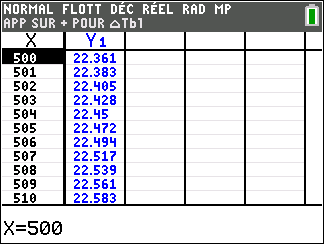
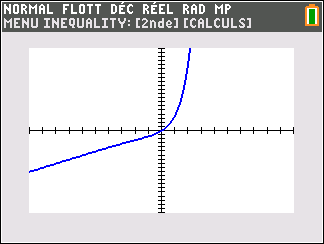
Lorsque les valeurs de x se rapprochent de +\infty, on peut voir dans le tableur ou sur la partie de la courbe située à droite que les valeurs de f(x) se rapprochent de +\infty.
A savoir :
lim_{x\to +\infty}\hspace{0.3cm}\sqrt{x}=+\infty
La fonction exponentielle
f(x)=e^x définie sur \mathbf{R}.
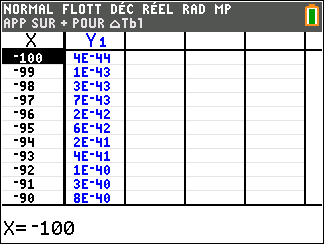
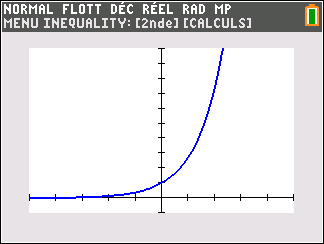
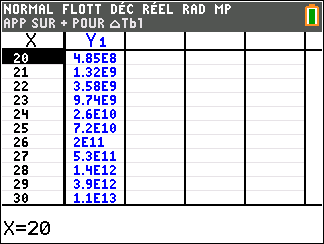
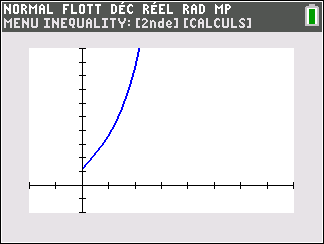
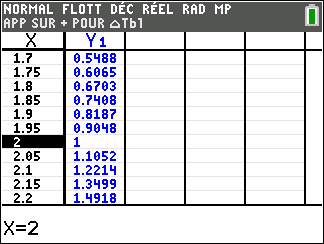
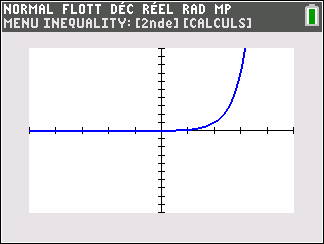
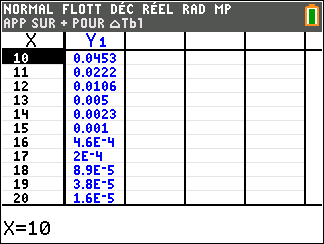
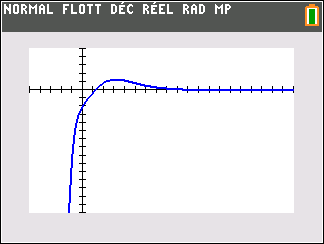
Lorsque les valeurs de x se rapprochent de -\infty, on peut voir dans le tableur de gauche en le lisant du bas vers le haut ou sur la partie de la courbe située à gauche que les valeurs de f(x) se rapprochent de 0.
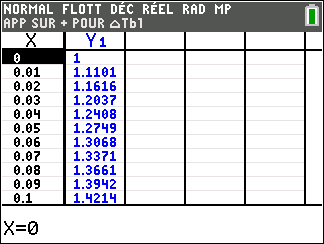
Lorsque les valeurs de x se rapprochent de +\infty, on peut voir dans le tableur de droite ou sur la partie de la courbe située à droite que les valeurs de f(x) se rapprochent de +\infty.
A savoir :
lim_{x\to -\infty}\hspace{0.3cm}e^x=0 et lim_{x\to +\infty}\hspace{0.3cm}e^x=+\infty
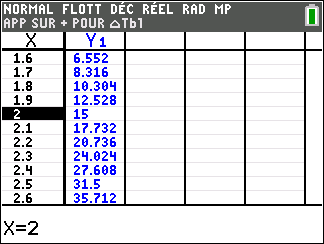
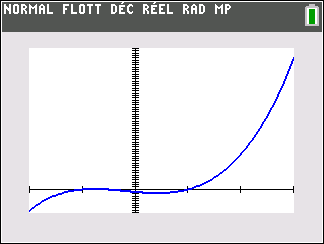
La fonction puissance
f(x)=x^n définie sur \mathbf{R} avec n\in \mathbf{N}^{*}
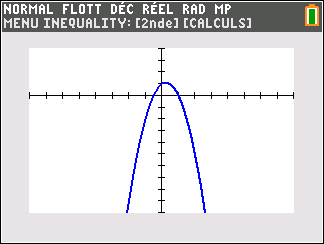
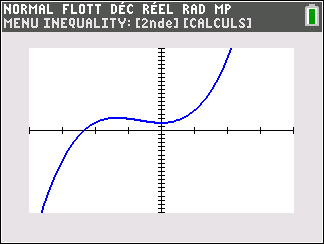
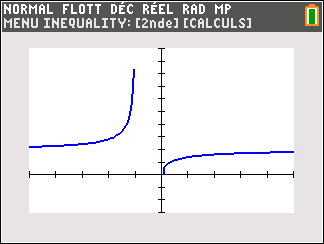
Si n est pair ( pour la figure, on a pris n=2)

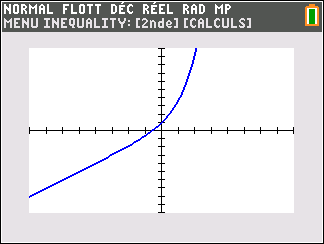
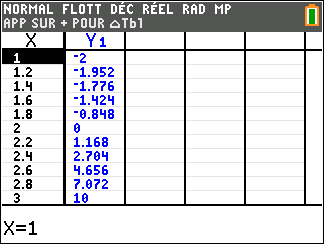
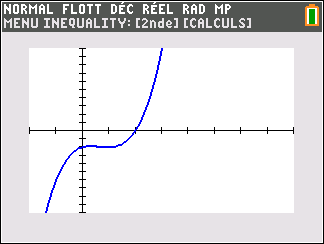
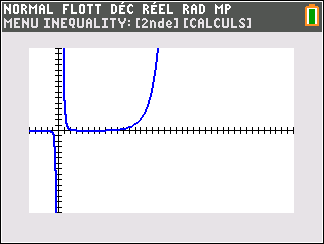
Si n est impair ( pour la figure, on a pris n=3)
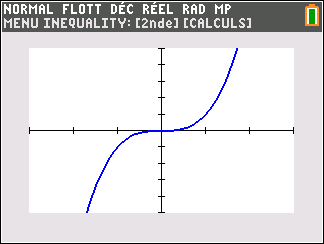
A savoir :
Si n est pair,
lim_{x\to -\infty}\hspace{0.3cm}x^n=+\infty et lim_{x\to +\infty}\hspace{0.3cm}x^n=+\infty
Si n est impair,
lim_{x\to -\infty}\hspace{0.3cm}x^n=-\infty et lim_{x\to +\infty}\hspace{0.3cm}x^n=+\infty
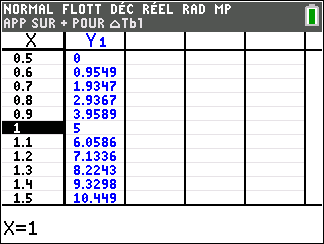
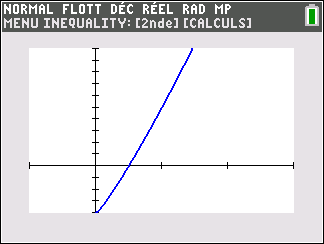
La fonction inverse d’une puissance
f(x)=\frac{1}{x^n} définie sur \mathbf{R}^{*} avec n\in \mathbf{N}^{*}
Si n est pair ( pour la figure, on a pris n=2)
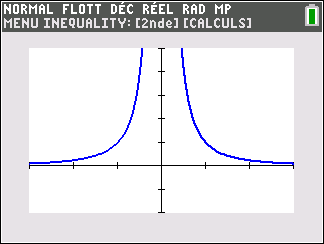
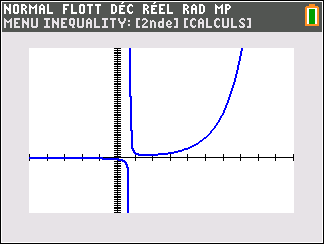
Si n est impair ( pour la figure, on a pris n=1)
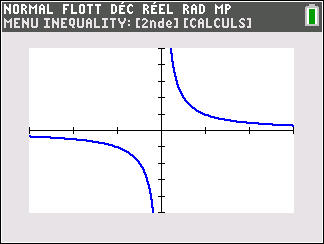
A savoir :
Si n est pair,
lim_{x\to -\infty}\hspace{0.3cm}\frac{1}{x^n}=0 , lim_{x\to 0^{-}}\hspace{0.3cm}\frac{1}{x^n}=+\infty , lim_{x\to 0^{+}}\hspace{0.3cm}\frac{1}{x^n}=+\infty et lim_{x\to +\infty}\hspace{0.3cm}\frac{1}{x^n}=0.
Si n est impair,
lim_{x\to -\infty}\hspace{0.3cm}\frac{1}{x^n}=0 , lim_{x\to 0^{-}}\hspace{0.3cm}\frac{1}{x^n}=-\infty , lim_{x\to 0^{+}}\hspace{0.3cm}\frac{1}{x^n}=+\infty et lim_{x\to +\infty}\hspace{0.3cm}\frac{1}{x^n}=0.
Opérations sur les limites
Tableaux
Dans ces quatre tableaux, f et g représentent deux fonctions et l et l’ représentent deux nombres réels.
Les propriétés suivantes sont valables quand on calcule une limite en -\infty, en +\infty et en en a où a désigne un nombre réel.
| \lim f= | l | l | l | +\infty | -\infty | +\infty |
| \lim g= | l’ | +\infty | -\infty | +\infty | -\infty | -\infty |
| \lim f+g= | l+l’ | +\infty | -\infty | +\infty | -\infty | Forme indéterminée |
Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.
| \lim f= | l | l\ne0 | \infty | 0 |
| \lim g= | l’ | \infty | \infty | \infty |
| \lim fg= | l\times l’ | \infty | \infty | Forme indéterminée |
Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.
Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.
| \lim f= | l | l\ne0 | l | \infty | \infty | 0 |
| \lim g= | l’\ne0 | 0 | \infty | l | \infty | 0 |
| \lim\frac{f}{g}= | \frac{l}{l’} | \infty | 0 | \infty | Forme indéterminée | Forme indéterminée |
Remarque
quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .
Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.
Si lim_{x\to a}\hspace{0.2cm}f(x)=b et lim_{X\to b}\hspace{0.2cm}g(X)=c alors lim_{x\to a}\hspace{0.2cm}g(f(x))=c
Exercice n°1 : limite d’une somme.
Calculer les limites suivantes.
- lim_{x\to -\infty}\hspace{0.2cm}x^2-x
2. lim_{x\to +\infty}\hspace{0.2cm}\frac{1}{x}+\sqrt{x}
3. lim_{x\to -\infty}\hspace{0.2cm}2x^2+x+1
4. lim_{x\to 0^{+}}\hspace{0.3cm}\frac{1}{x}+x
5. lim_{x\to -\infty}\hspace{0.2cm}e^x+x
6. lim_{x\to +\infty}\hspace{0.2cm}-2x^2+x+1
7. lim_{x\to 0}\hspace{0.2cm}e^x+\sqrt{x}
8. lim_{x\to 2}\hspace{0.3cm}x^3-2x^2+x-2
9. lim_{x\to -\infty}\hspace{0.3cm}x^3+2x^2+2
Exercice n°2 : limite d’un produit.
Calculer les limites suivantes.
- lim_{x\to -\infty}\hspace{0.2cm}x(e^x+1)
2. lim_{x\to +\infty}\hspace{0.2cm}x\sqrt{x}
3. lim_{x\to +\infty}\hspace{0.2cm}\frac{1}{x}(x-1)
4. lim_{x\to +\infty}\hspace{0.3cm}\sqrt{x}(2-x)
5. lim_{x\to 0^{+}}\hspace{0.2cm}e^x(1-\frac{1}{x^2})
6. lim_{x\to +\infty}\hspace{0.2cm}(x^3-2x+1)(1-\frac{1}{x^2})
7. lim_{x\to 0^{+}}\hspace{0.2cm}e^x(1+\frac{1}{x})
8. lim_{x\to 2}\hspace{0.3cm}(x^2-1)(2x+1)
9. lim_{x\to 1}\hspace{0.3cm}(\sqrt{x}+4)(2x-1)
Exercice n°3 : limite d’un quotient.
Calculer les limites suivantes.
- lim_{x\to 0}\hspace{0.2cm}\frac{5x-1}{x^2-3}
2. lim_{x\to -\infty}\hspace{0.2cm}\frac{3}{x^2-3}
3. lim_{x\to +\infty}\hspace{0.2cm}\frac{2x+1}{3x-2}
4. lim_{x\to -\infty}\hspace{0.3cm}\frac{e^x}{3x-2}
5. lim_{x\to 0}\hspace{0.2cm}\frac{x^2}{x-1}
6. lim_{x\to +\infty}\hspace{0.2cm}\frac{x}{\sqrt{x}}
7. lim_{x\to {+\infty}}\hspace{0.2cm}\frac{x^2}{x+1}
8. lim_{x\to -\infty}\hspace{0.3cm}\frac{x-1}{x^2-x+2}
9. lim_{x\to 1^{+}}\hspace{0.3cm}\frac{2x+2}{x-1}
Exercice n°4 : limite de fonction composée.
Calculer les limites suivantes.
- lim_{x\to 2}\hspace{0.2cm}e^{2x-4}
2. lim_{x\to -\infty}\hspace{0.2cm}(2x-1)^2
3. lim_{x\to +\infty}\hspace{0.2cm}\sqrt{3x^2+x+1}
4. lim_{x\to -\infty}\hspace{0.3cm}e^{6-x}
5. lim_{x\to 2^{-}}\hspace{0.2cm}\frac{1}{2-x}
6. lim_{x\to +\infty}\hspace{0.2cm}\sqrt{\frac{4x}{x+1}}
Théorèmes de comparaison et croissances comparées
Théorèmes de comparaison
On écrit les théorèmes quand x tend vers +\infty, ils sont aussi valables quand x tend vers -\infty.
f,g,h sont des fonctions définies sur un intervalle I.
- Si pour tout réel x de I, f(x)\geq g(x) et lim_{x\to +\infty}\hspace{0.3cm}g(x)=+\infty alors lim_{x\to +\infty}\hspace{0.3cm}f(x)=+\infty
- Si pour tout réel x de I, f(x)\leq g(x) et lim_{x\to +\infty}\hspace{0.3cm}g(x)=-\infty alors lim_{x\to +\infty}\hspace{0.3cm}f(x)=-\infty
- Théorème des gendarmes
Si pour tout réel x de I, f(x)\leq g(x)\leq h(x)
et si lim_{x\to +\infty}\hspace{0.3cm}f(x)=lim_{x\to+\infty}\hspace{0.3cm}h(x)=L
alors lim_{x\to +\infty}\hspace{0.3cm}g(x)=L
Exercice n°5 : théorèmes de comparaison.
f est la fonction définie par f(x)=x^2-2sinx
- Démontrer que f(x)\geq x^2-2
2. En déduire la limite de f en +\infty et -\infty
Exercice n°6 : théorèmes de comparaison.
f est la fonction définie par f(x)=-x-cos(x)
- Démontrer que f(x)\leq -x+1
2. En déduire la limite de f en +\infty.
Exercice n°7 : théorème des gendarmes.
f est la fonction définie par f(x)=\frac{3x+3}{cos(x)+2}
- Démontrer que x+1\leq f(x)\leq 3x+3 pour x>-1.
2. En déduire la limite de f en +\infty.
Croissances comparées
n un entier naturel non nul.
lim_{x\to +\infty}\hspace{0.3cm}\frac{e^x}{x}=+\infty , lim_{x\to -\infty}\hspace{0.3cm}xe^x=0\\lim_{x\to +\infty}\hspace{0.3cm}\frac{e^x}{x^n}=+\infty , lim_{x\to -\infty}\hspace{0.3cm}x^ne^x=0
Exercice n°8 : croissances comparées.
Calculer les limites suivantes.
- lim_{x\to +\infty}\hspace{0.2cm}\frac{e^{x}}{x^5}
2. lim_{x\to +\infty}\hspace{0.2cm}\frac{x^3-2}{e^{x}}
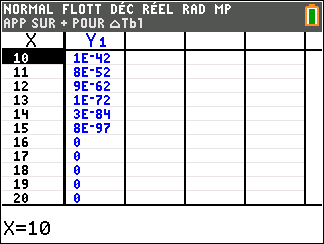
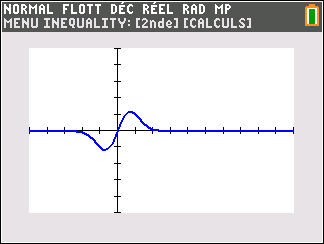
3. lim_{x\to +\infty}\hspace{0.2cm}xe^{1-x^2}
On pourra montrer que xe^{1-x^2}=\frac{e}{x}\times \frac{x^2}{e^{x^2}}.
4. lim_{x\to +\infty}\hspace{0.3cm}e^{x}-2x
5. lim_{x\to -\infty}\hspace{0.2cm}x+e^{-x}
On pourra montrer que x+e^{-x}=x(1+\frac{1}{xe^{x}}).
6. lim_{x\to +\infty}\hspace{0.2cm}xe^{1-x}
On pourra montrer que xe^{1-x}=e\times \frac{x}{e^{x}}.