logo

T. Limites et asymptotes.

Sommaire

Asymptote horizontale

Définition 

Si lim_{x\to+\infty}f(x)=l ou lim_{x\to-\infty}f(x)=l alors on dit que la droite d’équation y=l est une asymptote horizontale à la courbe représentative de la fonction f en +\infty ou en -\infty.

Exemple n°1 : la fonction inverse.

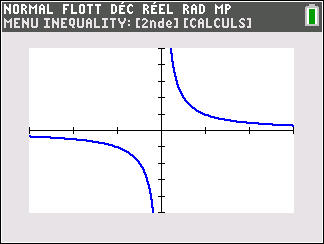
lim_{x\to-\infty}\frac{1}{x}=0 donc la droite d’équation y=0 ( c’est-à-dire l’axe des abscisses ) est une asymptote horizontale à la courbe représentative de la fontion inverse en -\infty.

lim_{x\to+\infty}\frac{1}{x}=0 donc la droite d’équation y=0 ( c’est-à-dire l’axe des abscisses ) est une asymptote horizontale à la courbe représentative de la fontion inverse en +\infty.

Exemple n°2 : la fonction exponentielle.

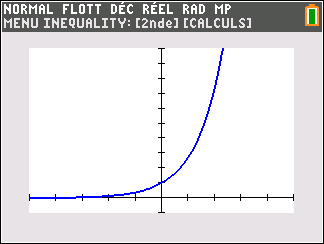
lim_{x\to-\infty}e^x=0 donc la droite d’équation y=0 ( c’est-à-dire l’axe des abscisses ) est une asymptote horizontale à la courbe représentative de la fontion exponentielle en -\infty.

Asymptote verticale

Définition 

Si \lim _{\substack{ x\to a\\x<a}}f(x)=+\infty ou -\infty ou si \lim _{\substack{ x\to a\\x>a}}f(x)=+\infty ou -\infty lim_{x\to-\infty}f(x)=l alors on dit que la droite d’équation x=a est une asymptote verticale à la courbe représentative de la fonction f.

Exemple n°3 : la fonction inverse.

 \lim _{\substack{ x\to 0\\x<0}}\frac{1}{x}=-\infty donc la droite d’équation x=0 ( l’axe des ordonnées ) est une asymptote verticale à la courbe représentative de la fonction inverse.

ou

\lim _{\substack{ x\to 0\\x>0}}\frac{1}{x}=+\infty donc la droite d’équation x=0 ( l’axe des ordonnées ) est une asymptote verticale à la courbe représentative de la fonction inverse.

Exercices

Exercice n°1

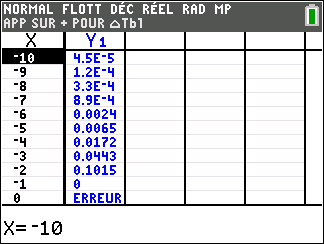
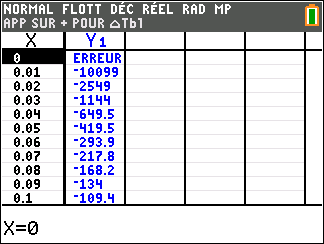
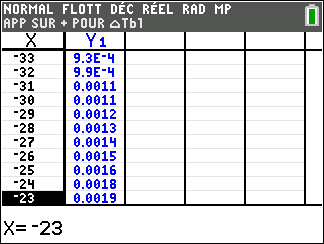
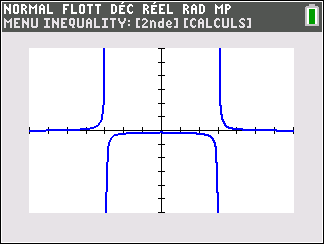
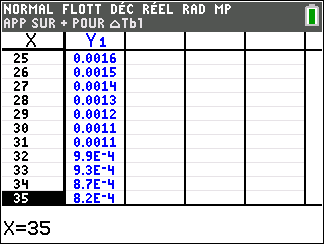
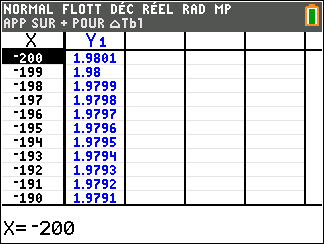
Soit la fonction f(x)=e^x(1-\frac{1}{x^2}) définie sur \mathbf{R}^{*}.

Voici sa courbe obtenue à l’aide de la calculatrice :

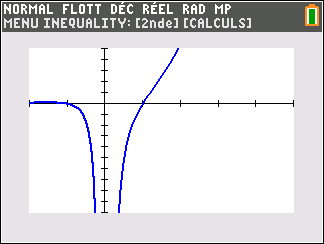
 Déterminer graphiquement les asymptotes éventuelles à la courbe C_f.

correction

Exercice n°2

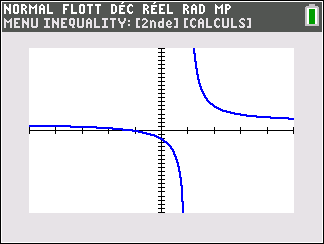
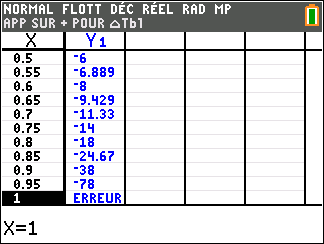
Soit la fonction f(x)=\frac{1}{2-x} définie sur \mathbf{R} privé de  2.

Voici sa courbe obtenue à l’aide de la calculatrice :

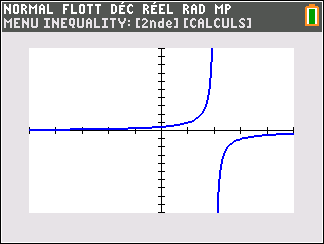
 Déterminer graphiquement les asymptotes éventuelles à la courbe C_f.

correction

Exercice n°3

Soit la fonction f(x)=\frac{1}{x^2-4} définie sur \mathbf{R} privé de  -2 et 2.

Voici sa courbe obtenue à l’aide de la calculatrice :

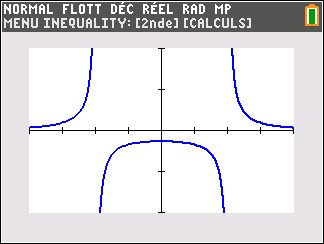
 Déterminer graphiquement les asymptotes éventuelles à la courbe C_f.

correction

Exercice n°4

Soit la fonction f(x)=(x^3-2x+1)(1-\frac{1}{x^2}) définie sur \mathbf{R} privé de  0.

Voici sa courbe obtenue à l’aide de la calculatrice :

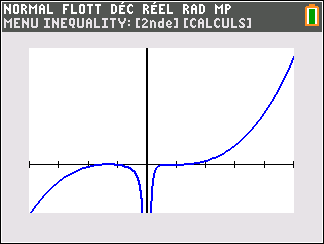
 Déterminer graphiquement les asymptotes éventuelles à la courbe C_f.

correction

Exercice n°5

Soit la fonction f(x)=e^x(1-\frac{1}{x^2}) définie sur \mathbf{R}^{*}.

  1. a.Calculer  \lim _{ x\to -\infty}f(x)
correction

 b. En déduire l’équation de l’asymptote horizontale à la courbe C_f en -\infty  .

correction

2.a.Calculer  \lim _{\substack{ x\to 0\\x>0}}f(x)

correction

 b. En déduire l’équation de l’asymptote verticale à la courbe C_f.

correction

Exercice n°6

Soit la fonction f(x)=\frac{1}{x^2-9} définie sur \mathbf{R} privé de -3 et 3 .

  1. a.Calculer  \lim _{ x\to -\infty}f(x)
correction

 b. En déduire l’équation de l’asymptote horizontale à la courbe C_f en -\infty  .

correction

2.a.Calculer  \lim _{\substack{ x\to -3\\x<-3}}f(x) et calculer  \lim _{\substack{ x\to -3\\x>-3}}f(x)

correction en -3^{-}
correction en -3^{+}

 b. En déduire l’équation de l’asymptote verticale à la courbe C_f.

correction

3.a.Calculer  \lim _{\substack{ x\to 3\\x<3}}f(x) et calculer  \lim _{\substack{ x\to 3\\x>3}}f(x)

correction en 3^{-}
correction en 3^{+}

 b. En déduire l’équation de l’asymptote verticale à la courbe C_f.

correction

4.a.Calculer  \lim _{ x\to +\infty}f(x)

correction

 b. En déduire l’équation de l’asymptote horizontale à la courbe C_f en +\infty.

correction

Exercice n°7

Soit la fonction f(x)=\frac{2x+2}{x-1} définie sur \mathbf{R} privé de 1.

  1. a.Calculer  \lim _{ x\to -\infty}f(x)
correction

 b. En déduire l’équation de l’asymptote horizontale à la courbe C_f en -\infty  .

correction

2.a.Calculer  \lim _{\substack{ x\to 1\\x<1}}f(x) et calculer  \lim _{\substack{ x\to 1\\x>1}}f(x)

correction en 1^{-}
correction en 1^{+}

 b. En déduire l’équation de l’asymptote verticale à la courbe C_f.

correction

3.a.Calculer  \lim _{ x\to +\infty}f(x)

correction

 b. En déduire l’équation de l’asymptote horizontale à la courbe C_f en +\infty.

correction

©2020 – Math’O karé SAS

  • La courbe se rapproche très près de l’axe des abscisses au voisinage de -\infty donc :

l’axe des abscisses, c’est-à-dire la droite d’équation y=0 est asymptote horizontale à la courbe en  -\infty

  • La courbe se rapproche très près de l’axe des ordonnées  donc :

l’axe des ordonnées, c’est-à-dire la droite d’équation x=0 est asymptote verticale à la courbe

  • La courbe se rapproche très près de l’axe des abscisses au voisinage de -\infty donc :

l’axe des abscisses, c’est-à-dire la droite d’équation y=0 est asymptote horizontale à la courbe en  -\infty

  • On peut imaginer que la courbe se rapproche très près de la droite verticale passant par la graduation 2 donc :

la droite d’équation x=2 est asymptote verticale à la courbe

  • La courbe se rapproche très près de l’axe des abscisses au voisinage de +\infty donc :

l’axe des abscisses, c’est-à-dire la droite d’équation y=0 est asymptote horizontale à la courbe en  +\infty

  • La courbe se rapproche très près de l’axe des abscisses au voisinage de -\infty donc :

l’axe des abscisses, c’est-à-dire la droite d’équation y=0 est asymptote horizontale à la courbe en  -\infty

  • On peut imaginer que la courbe se rapproche très près de la droite verticale passant par la graduation -2 donc :

la droite d’équation x=-2 est asymptote verticale à la courbe

  • On peut imaginer que la courbe se rapproche très près de la droite verticale passant par la graduation 2 donc :

la droite d’équation x=2 est asymptote verticale à la courbe

  • La courbe se rapproche très près de l’axe des abscisses au voisinage de +\infty donc :

l’axe des abscisses, c’est-à-dire la droite d’équation y=0 est asymptote horizontale à la courbe en  +\infty

  • La courbe se rapproche très près de l’axe des ordonnées  donc :

l’axe des ordonnées, c’est-à-dire la droite d’équation x=0 est asymptote verticale à la courbe

On veut calculer lim_{x\to -\infty}\hspace{0.2cm}e^x(1-\frac{1}{x^2}).

Regardons d’abord avec le tableur et la courbe de la calculatrice, vers quelle valeur se rapprochent les f(x) quand les x se rapprochent de -\infty.

Il semble que les  f(x) se rapprochent de 0.

La fonction est le produit de 2 fonctions, cliquer sur + La fonction est un produit, fg.

\lim f=lll+\infty-\infty+\infty
\lim g=l’+\infty-\infty+\infty-\infty-\infty
\lim f+g=l+l’+\infty-\infty+\infty-\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.

\lim f=ll\ne0\infty0
\lim g=l’\infty\infty\infty
\lim fg=l\times l’\infty\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

\lim f=ll\ne0l\infty\infty0
\lim g=l’\ne00\inftyl\infty0
\lim\frac{f}{g}=\frac{l}{l’}\infty0\inftyForme indéterminéeForme indéterminée

Remarque

quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

Si lim_{x\to a}\hspace{0.2cm}f(x)=b et lim_{X\to b}\hspace{0.2cm}g(X)=c alors lim_{x\to a}\hspace{0.2cm}g(f(x))=c

lim_{x\to -\infty}\hspace{0.2cm}e^x=0.

lim_{x\to -\infty}\hspace{0.2cm}{x^2}=+\infty\\lim_{x\to -\infty}\hspace{0.2cm}\frac{1}{x^2}=0\\lim_{x\to -\infty}\hspace{0.2cm}-\frac{1}{x^2}=0\\lim_{x\to -\infty}\hspace{0.2cm}1-\frac{1}{x^2}=1

Par produit , lim_{x\to -\infty}\hspace{0.2cm}e^x(1-\frac{1}{x^2})=0.

Donc lim_{x\to -\infty}\hspace{0.2cm}f(x)=0.

 

 

On a montré dans la question précédente que : lim_{x\to -\infty}\hspace{0.2cm}f(x)=0.

Donc la droite d’équation y=0 ( l’axe des abscisses) est asymptote horizontale à la courbe C_f en -\infty.

On veut calculer \lim _{\substack{ x\to 0\\x>0}}f(x).

Regardons d’abord avec le tableur et la courbe de la calculatrice, vers quelle valeur se rapprochent les f(x) quand les x se rapprochent de 0 par valeurs in.

Il semble que les  f(x) se rapprochent de -\infty.

La fonction est le produit de 2 fonctions, cliquer sur + La fonction est un produit, fg.

\lim f=lll+\infty-\infty+\infty
\lim g=l’+\infty-\infty+\infty-\infty-\infty
\lim f+g=l+l’+\infty-\infty+\infty-\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.

\lim f=ll\ne0\infty0
\lim g=l’\infty\infty\infty
\lim fg=l\times l’\infty\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

\lim f=ll\ne0l\infty\infty0
\lim g=l’\ne00\inftyl\infty0
\lim\frac{f}{g}=\frac{l}{l’}\infty0\inftyForme indéterminéeForme indéterminée

Remarque

quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

Si lim_{x\to a}\hspace{0.2cm}f(x)=b et lim_{X\to b}\hspace{0.2cm}g(X)=c alors lim_{x\to a}\hspace{0.2cm}g(f(x))=c

lim_{\substack{ x\to 0\\x>0}}\hspace{0.2cm}e^x=1.

lim_{\substack{ x\to 0\\x>0}}\hspace{0.2cm}{x^2}=0^{+}\\lim_{\substack{ x\to 0\\x>0}}\hspace{0.2cm}\frac{1}{x^2}=+\infty\\lim_{\substack{ x\to 0\\x>0}}\hspace{0.2cm}-\frac{1}{x^2}=-\infty\\lim_{\substack{ x\to 0\\x>0}}\hspace{0.2cm}1-\frac{1}{x^2}=-\infty

Par produit , lim_{\substack{ x\to 0\\x>0}}\hspace{0.2cm}e^x(1-\frac{1}{x^2})=-\infty.

Donc lim_{\substack{ x\to 0\\x>0}}\hspace{0.2cm}f(x)=-\infty

 

 

On a montré dans la question précédente que :  lim_{\substack{ x\to 0\\x>0}}\hspace{0.2cm}f(x)=-\infty

Donc la droite d’équation x=0 ( c’est_à_dire l’axe des oronnées ) est asymptote verticale à la courbe.

On veut calculer lim_{x\to -\infty}\hspace{0.2cm}\frac{1}{x^2-9}.

Regardons d’abord avec le tableur et la courbe de la calculatrice, vers quelle valeur se rapprochent les f(x) quand les x se rapprochent de -\infty.

Il semble que les  f(x) se rapprochent de 0.

La fonction est le quotient de 2 fonctions, cliquer sur + La fonction est un quotient, f/g.

\lim f=lll+\infty-\infty+\infty
\lim g=l’+\infty-\infty+\infty-\infty-\infty
\lim f+g=l+l’+\infty-\infty+\infty-\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.

\lim f=ll\ne0\infty0
\lim g=l’\infty\infty\infty
\lim fg=l\times l’\infty\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

\lim f=ll\ne0l\infty\infty0
\lim g=l’\ne00\inftyl\infty0
\lim\frac{f}{g}=\frac{l}{l’}\infty0\inftyForme indéterminéeForme indéterminée

Remarque

quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

Si lim_{x\to a}\hspace{0.2cm}f(x)=b et lim_{X\to b}\hspace{0.2cm}g(X)=c alors lim_{x\to a}\hspace{0.2cm}g(f(x))=c

lim_{x\to -\infty}\hspace{0.2cm}1=1
lim_{x\to -\infty}\hspace{0.2cm}x^2=+\infty\\lim_{x\to -\infty}\hspace{0.2cm}x^2-9=+\infty

Par quotient , lim_{x\to -\infty}\hspace{0.2cm}\frac{1}{x^2-9}=0.

Donc lim_{x\to -\infty}\hspace{0.2cm}f(x)=0.

 

 

On a montré dans la question précédente que : lim_{x\to -\infty}\hspace{0.2cm}f(x)=0.

Donc la droite d’équation y=0 ( l’axe des abscisses) est asymptote horizontale à la courbe C_f en -\infty.

On veut calculer \lim _{\substack{ x\to -3\\x<-3}}\frac{1}{x^2-9} 

Regardons d’abord avec le tableur et la courbe de la calculatrice, vers quelle valeur se rapprochent les f(x) quand les x se rapprochent de -3 par valeurs inférieures.

Il semble que les  f(x) se rapprochent de +\infty.

La fonction est le quotient de 2 fonctions, cliquer sur + La fonction est un quotient, f/g.

\lim f=lll+\infty-\infty+\infty
\lim g=l’+\infty-\infty+\infty-\infty-\infty
\lim f+g=l+l’+\infty-\infty+\infty-\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.

\lim f=ll\ne0\infty0
\lim g=l’\infty\infty\infty
\lim fg=l\times l’\infty\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

\lim f=ll\ne0l\infty\infty0
\lim g=l’\ne00\inftyl\infty0
\lim\frac{f}{g}=\frac{l}{l’}\infty0\inftyForme indéterminéeForme indéterminée

Remarque

quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

Si lim_{x\to a}\hspace{0.2cm}f(x)=b et lim_{X\to b}\hspace{0.2cm}g(X)=c alors lim_{x\to a}\hspace{0.2cm}g(f(x))=c

lim_{\substack{ x\to -3\\x<-3}}\hspace{0.3cm}1=1

lim_{\substack{ x\to -3\\x<-3}}\hspace{0.3cm}x^2-9=0^{+}, comme x<-3 alors x^2-9 est positif d’après le tableau ci-dessous

Par quotient , lim_{\substack{ x\to -3\\x<-3}}\hspace{0.3cm}\frac{1}{x^2-9}=+\infty

Donc lim_{\substack{ x\to -3\\x<-3}}\hspace{0.3cm}f(x)=+\infty

 

 

On veut calculer \lim _{\substack{ x\to -3\\x>-3}}\frac{1}{x^2-9} 

Regardons d’abord avec le tableur et la courbe de la calculatrice, vers quelle valeur se rapprochent les f(x) quand les x se rapprochent de -3 par valeurs supérieures.

Il semble que les  f(x) se rapprochent de -\infty.

La fonction est le quotient de 2 fonctions, cliquer sur + La fonction est un quotient, f/g.

\lim f=lll+\infty-\infty+\infty
\lim g=l’+\infty-\infty+\infty-\infty-\infty
\lim f+g=l+l’+\infty-\infty+\infty-\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.

\lim f=ll\ne0\infty0
\lim g=l’\infty\infty\infty
\lim fg=l\times l’\infty\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

\lim f=ll\ne0l\infty\infty0
\lim g=l’\ne00\inftyl\infty0
\lim\frac{f}{g}=\frac{l}{l’}\infty0\inftyForme indéterminéeForme indéterminée

Remarque

quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

Si lim_{x\to a}\hspace{0.2cm}f(x)=b et lim_{X\to b}\hspace{0.2cm}g(X)=c alors lim_{x\to a}\hspace{0.2cm}g(f(x))=c

lim_{\substack{ x\to -3\\x>-3}}\hspace{0.3cm}1=1

lim_{\substack{ x\to -3\\x>-3}}\hspace{0.3cm}x^2-9=0^{-}, comme x>-3 alors x^2-9 est négatif d’après le tableau ci-dessous

Par quotient , lim_{\substack{ x\to -3\\x<-3}}\hspace{0.3cm}\frac{1}{x^2-9}=-\infty.

Donc lim_{\substack{ x\to -3\\x<-3}}\hspace{0.3cm}f(x)=-\infty

 

 

On a montré dans la question précédente que :  lim_{\substack{ x\to -3\\x<-3}}\hspace{0.2cm}f(x)=+\infty

Donc la droite d’équation x=-3 est asymptote verticale à la courbe.

On veut calculer \lim _{\substack{ x\to 3\\x<3}}\frac{1}{x^2-9} 

Regardons d’abord avec le tableur et la courbe de la calculatrice, vers quelle valeur se rapprochent les f(x) quand les x se rapprochent de 3 par valeurs inférieures.

Il semble que les  f(x) se rapprochent de -\infty.

La fonction est le quotient de 2 fonctions, cliquer sur + La fonction est un quotient, f/g.

\lim f=lll+\infty-\infty+\infty
\lim g=l’+\infty-\infty+\infty-\infty-\infty
\lim f+g=l+l’+\infty-\infty+\infty-\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.

\lim f=ll\ne0\infty0
\lim g=l’\infty\infty\infty
\lim fg=l\times l’\infty\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

\lim f=ll\ne0l\infty\infty0
\lim g=l’\ne00\inftyl\infty0
\lim\frac{f}{g}=\frac{l}{l’}\infty0\inftyForme indéterminéeForme indéterminée

Remarque

quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

Si lim_{x\to a}\hspace{0.2cm}f(x)=b et lim_{X\to b}\hspace{0.2cm}g(X)=c alors lim_{x\to a}\hspace{0.2cm}g(f(x))=c

lim_{\substack{ x\to 3\\x<3}}\hspace{0.3cm}1=1

lim_{\substack{ x\to 3\\x<3}}\hspace{0.3cm}x^2-9=0^{-}, comme x<3 alors x^2-9 est négatif d’après le tableau ci-dessous

Par quotient , lim_{\substack{ x\to 3\\x<3}}\hspace{0.3cm}\frac{1}{x^2-9}=-\infty

Donc lim_{\substack{ x\to 3\\x<3}}\hspace{0.3cm}f(x)=-\infty

 

 

On veut calculer \lim _{\substack{ x\to 3\\x>3}}\frac{1}{x^2-9} 

Regardons d’abord avec le tableur et la courbe de la calculatrice, vers quelle valeur se rapprochent les f(x) quand les x se rapprochent de 3 par valeurs supérieures.

Il semble que les  f(x) se rapprochent de +\infty.

La fonction est le quotient de 2 fonctions, cliquer sur + La fonction est un quotient, f/g.

\lim f=lll+\infty-\infty+\infty
\lim g=l’+\infty-\infty+\infty-\infty-\infty
\lim f+g=l+l’+\infty-\infty+\infty-\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.

\lim f=ll\ne0\infty0
\lim g=l’\infty\infty\infty
\lim fg=l\times l’\infty\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

\lim f=ll\ne0l\infty\infty0
\lim g=l’\ne00\inftyl\infty0
\lim\frac{f}{g}=\frac{l}{l’}\infty0\inftyForme indéterminéeForme indéterminée

Remarque

quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

Si lim_{x\to a}\hspace{0.2cm}f(x)=b et lim_{X\to b}\hspace{0.2cm}g(X)=c alors lim_{x\to a}\hspace{0.2cm}g(f(x))=c

lim_{\substack{ x\to 3\\x>3}}\hspace{0.3cm}1=1

lim_{\substack{ x\to 3\\x>3}}\hspace{0.3cm}x^2-9=0^{+}, comme x>3 alors x^2-9 est négatif d’après le tableau ci-dessous

Par quotient , lim_{\substack{ x\to 3\\x>3}}\hspace{0.3cm}\frac{1}{x^2-9}=+\infty

Donc lim_{\substack{ x\to 3\\x>3}}\hspace{0.3cm}f(x)=+\infty

 

 

On a montré dans la question précédente que :  lim_{\substack{ x\to 3\\x<3}}\hspace{0.2cm}f(x)=-\infty

Donc la droite d’équation x=3 est asymptote verticale à la courbe.

On veut calculer lim_{x\to +\infty}\hspace{0.2cm}\frac{1}{x^2-9}.

Regardons d’abord avec le tableur et la courbe de la calculatrice, vers quelle valeur se rapprochent les f(x) quand les x se rapprochent de +\infty.

Il semble que les  f(x) se rapprochent de 0.

La fonction est le quotient de 2 fonctions, cliquer sur + La fonction est un quotient, f/g.

\lim f=lll+\infty-\infty+\infty
\lim g=l’+\infty-\infty+\infty-\infty-\infty
\lim f+g=l+l’+\infty-\infty+\infty-\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.

\lim f=ll\ne0\infty0
\lim g=l’\infty\infty\infty
\lim fg=l\times l’\infty\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

\lim f=ll\ne0l\infty\infty0
\lim g=l’\ne00\inftyl\infty0
\lim\frac{f}{g}=\frac{l}{l’}\infty0\inftyForme indéterminéeForme indéterminée

Remarque

quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

Si lim_{x\to a}\hspace{0.2cm}f(x)=b et lim_{X\to b}\hspace{0.2cm}g(X)=c alors lim_{x\to a}\hspace{0.2cm}g(f(x))=c

lim_{x\to +\infty}\hspace{0.2cm}1=1
lim_{x\to +\infty}\hspace{0.2cm}x^2=+\infty\\lim_{x\to +\infty}\hspace{0.2cm}x^2-9=+\infty

Par quotient , lim_{x\to +\infty}\hspace{0.2cm}\frac{1}{x^2-9}=0.

Donc lim_{x\to +\infty}\hspace{0.2cm}f(x)=0.

 

 

On a montré dans la question précédente que : lim_{x\to +\infty}\hspace{0.2cm}f(x)=0.

Donc la droite d’équation y=0 ( l’axe des abscisses) est asymptote horizontale à la courbe C_f en +\infty.

On veut calculer lim_{x\to -\infty}\hspace{0.2cm}\frac{2x+2}{x-1}.

Regardons d’abord avec le tableur et la courbe de la calculatrice, vers quelle valeur se rapprochent les f(x) quand les x se rapprochent de -\infty.

Il semble que les  f(x) se rapprochent de 2.

La fonction est le quotient de 2 fonctions, cliquer sur + La fonction est un quotient, f/g.

\lim f=lll+\infty-\infty+\infty
\lim g=l’+\infty-\infty+\infty-\infty-\infty
\lim f+g=l+l’+\infty-\infty+\infty-\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.

\lim f=ll\ne0\infty0
\lim g=l’\infty\infty\infty
\lim fg=l\times l’\infty\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

\lim f=ll\ne0l\infty\infty0
\lim g=l’\ne00\inftyl\infty0
\lim\frac{f}{g}=\frac{l}{l’}\infty0\inftyForme indéterminéeForme indéterminée

Remarque

quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

Si lim_{x\to a}\hspace{0.2cm}f(x)=b et lim_{X\to b}\hspace{0.2cm}g(X)=c alors lim_{x\to a}\hspace{0.2cm}g(f(x))=c

lim_{x\to -\infty}\hspace{0.2cm}2x+2= -\infty

lim_{x\to -\infty}\hspace{0.2cm}x-1=-\infty

Le théorème sur le quotient ne permet pas de conclure car on obtient la forme indéterminée, -\infty /-\infty.

Obtenir une forme indéterminée ne signifie pas qu’il n’y a pas de limite, cela signifie que le théorème ne permet pas de conclure. On change la forme de \frac{2x+2}{x-1}. On est en \infty et c’est le quotient de deux polynômes, il faut mettre en facteur les puissances de x de plus haut degré. x au numérateur et x au dénominateur.

\frac{2x+2}{x-1}=\frac {x(2+\frac{2}{x})}{x(1-\frac{1}{x})}

On simplifie par x

\frac{2x+2}{x-1}=\frac {2+\frac{2}{x}}{1-\frac{1}{x}}

La fonction est le quotient de 2 fonctions, cliquer sur + La fonction est un quotient, f/g.

lim_{x\to -\infty}\hspace{0.2cm}\frac{1}{x}=0\\lim_{x\to -\infty}\hspace{0.2cm}\frac{2}{x}=0\\lim_{x\to -\infty}\hspace{0.2cm}2+\frac{2}{x}=2
lim_{x\to -\infty}\hspace{0.2cm}\frac{1}{x}=0\\lim_{x\to -\infty}\hspace{0.2cm}1-\frac{1}{x}=1

 

Par quotient , lim_{x\to -\infty}\hspace{0.2cm}\frac {2+\frac{2}{x}}{1-\frac{1}{x}}=2.

Donc lim_{x\to -\infty}\hspace{0.2cm}f(x)=2.

 

 

On a montré dans la question précédente que : lim_{x\to -\infty}\hspace{0.2cm}f(x)=2.

Donc la droite d’équation y=2 est asymptote horizontale à la courbe C_f en -\infty.

On veut calculer lim_{\substack{ x\to 1\\x<1}}\hspace{0.3cm}\frac{2x+2}{x-1}.

Regardons d’abord avec le tableur et la courbe de la calculatrice, vers quelle valeur se rapprochent les f(x) quand les x se rapprochent de 1 par valeurs inférieures.

Il semble que les  f(x) se rapprochent de -\infty.

La fonction est le quotient de 2 fonctions, cliquer sur + La fonction est un quotient, f/g.

\lim f=lll+\infty-\infty+\infty
\lim g=l’+\infty-\infty+\infty-\infty-\infty
\lim f+g=l+l’+\infty-\infty+\infty-\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.

\lim f=ll\ne0\infty0
\lim g=l’\infty\infty\infty
\lim fg=l\times l’\infty\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

\lim f=ll\ne0l\infty\infty0
\lim g=l’\ne00\inftyl\infty0
\lim\frac{f}{g}=\frac{l}{l’}\infty0\inftyForme indéterminéeForme indéterminée

Remarque

quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

Si lim_{x\to a}\hspace{0.2cm}f(x)=b et lim_{X\to b}\hspace{0.2cm}g(X)=c alors lim_{x\to a}\hspace{0.2cm}g(f(x))=c

lim_{\substack{ x\to 1\\x<1}}\hspace{0.3cm}2x+2=2\times 1+2=4

lim_{\substack{ x\to 1\\x<1}}\hspace{0.3cm}x-1=0^{-}, comme x<1 alors x-1<0 donc négatif. On peut aussi utiliser le tableau de signes ci-dessous.

Par quotient , lim_{x\to 1^{-}}\hspace{0.3cm}\frac{2x+2}{x-1}=-\infty.

Donc lim_{x\to 1^{-}}\hspace{0.3cm}f(x)=-\infty

 

 

On veut calculer lim_{\substack{ x\to 1\\x>1}}\hspace{0.3cm}\frac{2x+2}{x-1}.

Regardons d’abord avec le tableur et la courbe de la calculatrice, vers quelle valeur se rapprochent les f(x) quand les x se rapprochent de 1 par valeurs supérieures.

Il semble que les  f(x) se rapprochent de +\infty.

La fonction est le quotient de 2 fonctions, cliquer sur + La fonction est un quotient, f/g.

\lim f=lll+\infty-\infty+\infty
\lim g=l’+\infty-\infty+\infty-\infty-\infty
\lim f+g=l+l’+\infty-\infty+\infty-\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.

\lim f=ll\ne0\infty0
\lim g=l’\infty\infty\infty
\lim fg=l\times l’\infty\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

\lim f=ll\ne0l\infty\infty0
\lim g=l’\ne00\inftyl\infty0
\lim\frac{f}{g}=\frac{l}{l’}\infty0\inftyForme indéterminéeForme indéterminée

Remarque

quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

Si lim_{x\to a}\hspace{0.2cm}f(x)=b et lim_{X\to b}\hspace{0.2cm}g(X)=c alors lim_{x\to a}\hspace{0.2cm}g(f(x))=c

lim_{\substack{ x\to 1\\x>1}}\hspace{0.3cm}2x+2=2\times 1+2=4

 

lim_{\substack{ x\to 1\\x>1}}\hspace{0.3cm}x-1=0^{+}, comme x>1 alors x-1>0 donc positif. On peut aussi utiliser le tableau de signes ci-dessous.

Par quotient , lim_{x\to 1^{+}}\hspace{0.3cm}\frac{2x+2}{x-1}=+\infty.

Donc lim_{x\to 1^{+}}\hspace{0.3cm}f(x)=+\infty

 

 

On a montré dans la question précédente que :  lim_{\substack{ x\to 1\\x<1}}\hspace{0.2cm}f(x)=-\infty

Donc la droite d’équation x=1 est asymptote verticale à la courbe.

On veut calculer lim_{x\to +\infty}\hspace{0.2cm}\frac{2x+2}{x-1}.

Regardons d’abord avec le tableur et la courbe de la calculatrice, vers quelle valeur se rapprochent les f(x) quand les x se rapprochent de +\infty.

Il semble que les  f(x) se rapprochent de 2.

La fonction est le quotient de 2 fonctions, cliquer sur + La fonction est un quotient, f/g.

\lim f=lll+\infty-\infty+\infty
\lim g=l’+\infty-\infty+\infty-\infty-\infty
\lim f+g=l+l’+\infty-\infty+\infty-\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.

\lim f=ll\ne0\infty0
\lim g=l’\infty\infty\infty
\lim fg=l\times l’\infty\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

\lim f=ll\ne0l\infty\infty0
\lim g=l’\ne00\inftyl\infty0
\lim\frac{f}{g}=\frac{l}{l’}\infty0\inftyForme indéterminéeForme indéterminée

Remarque

quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

Si lim_{x\to a}\hspace{0.2cm}f(x)=b et lim_{X\to b}\hspace{0.2cm}g(X)=c alors lim_{x\to a}\hspace{0.2cm}g(f(x))=c

lim_{x\to+\infty}\hspace{0.2cm}2x+2= +\infty

lim_{x\to +\infty}\hspace{0.2cm}x-1=+\infty

Le théorème sur le quotient ne permet pas de conclure car on obtient la forme indéterminée, +\infty /+\infty.

Obtenir une forme indéterminée ne signifie pas qu’il n’y a pas de limite, cela signifie que le théorème ne permet pas de conclure. On change la forme de \frac{2x+2}{x-1}. On est en \infty et c’est le quotient de deux polynômes, il faut mettre en facteur les puissances de x de plus haut degré. x au numérateur et x au dénominateur.

\frac{2x+2}{x-1}=\frac {x(2+\frac{2}{x})}{x(1-\frac{1}{x})}

On simplifie par x

\frac{2x+2}{x-1}=\frac {2+\frac{2}{x}}{1-\frac{1}{x}}

La fonction est le quotient de 2 fonctions, cliquer sur + La fonction est un quotient, f/g.

lim_{x\to +\infty}\hspace{0.2cm}\frac{1}{x}=0\\lim_{x\to +\infty}\hspace{0.2cm}\frac{2}{x}=0\\lim_{x\to +\infty}\hspace{0.2cm}2+\frac{2}{x}=2
lim_{x\to +\infty}\hspace{0.2cm}\frac{1}{x}=0\\lim_{x\to +\infty}\hspace{0.2cm}1-\frac{1}{x}=1

Par quotient , lim_{x\to +\infty}\hspace{0.2cm}\frac {2+\frac{2}{x}}{1-\frac{1}{x}}=2.

Donc lim_{x\to +\infty}\hspace{0.2cm}f(x)=2.

 

 

On a montré dans la question précédente que : lim_{x\to +\infty}\hspace{0.2cm}f(x)=2.

Donc la droite d’équation y=2 est asymptote horizontale à la courbe C_f en +\infty.

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.