Intégrale d’une fonction continue et positive
Sommaire
Définition
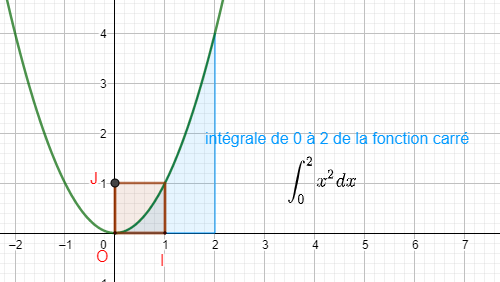
On appelle unité d’aire (u.a.) l’aire du rectangle de côtés [OI] et [OJ].
Soit f une fonction continue et positive sur un intervalle [a;b].
On appelle intégrale de a à b de f , l’aire exprimée en u.a. délimitée par la courbe C_f , l’axe des abscisses et les droites verticales d’équations x=a et x=b.
Cette intégrale se note \int_a^b f(x)\hspace{0.05cm}dx
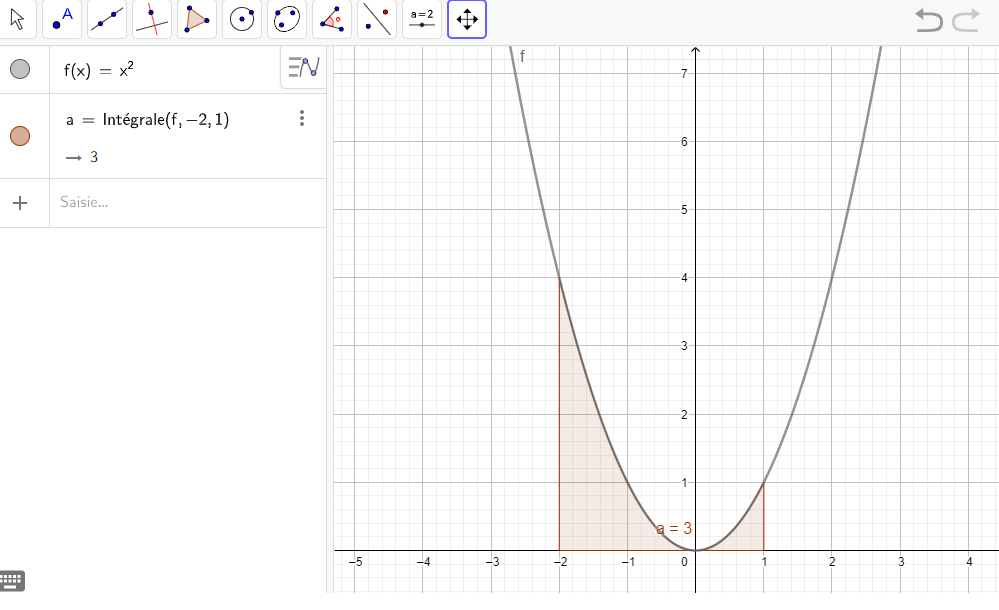
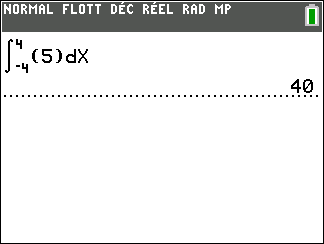
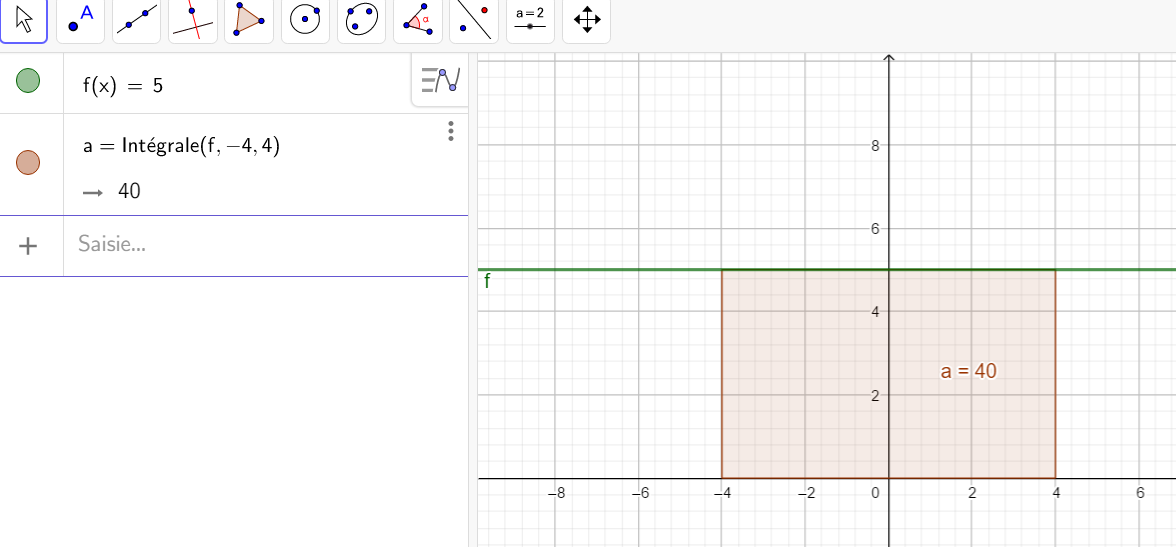
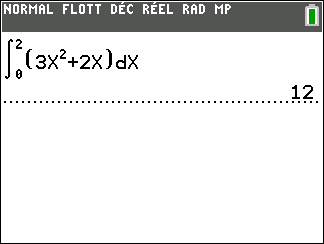
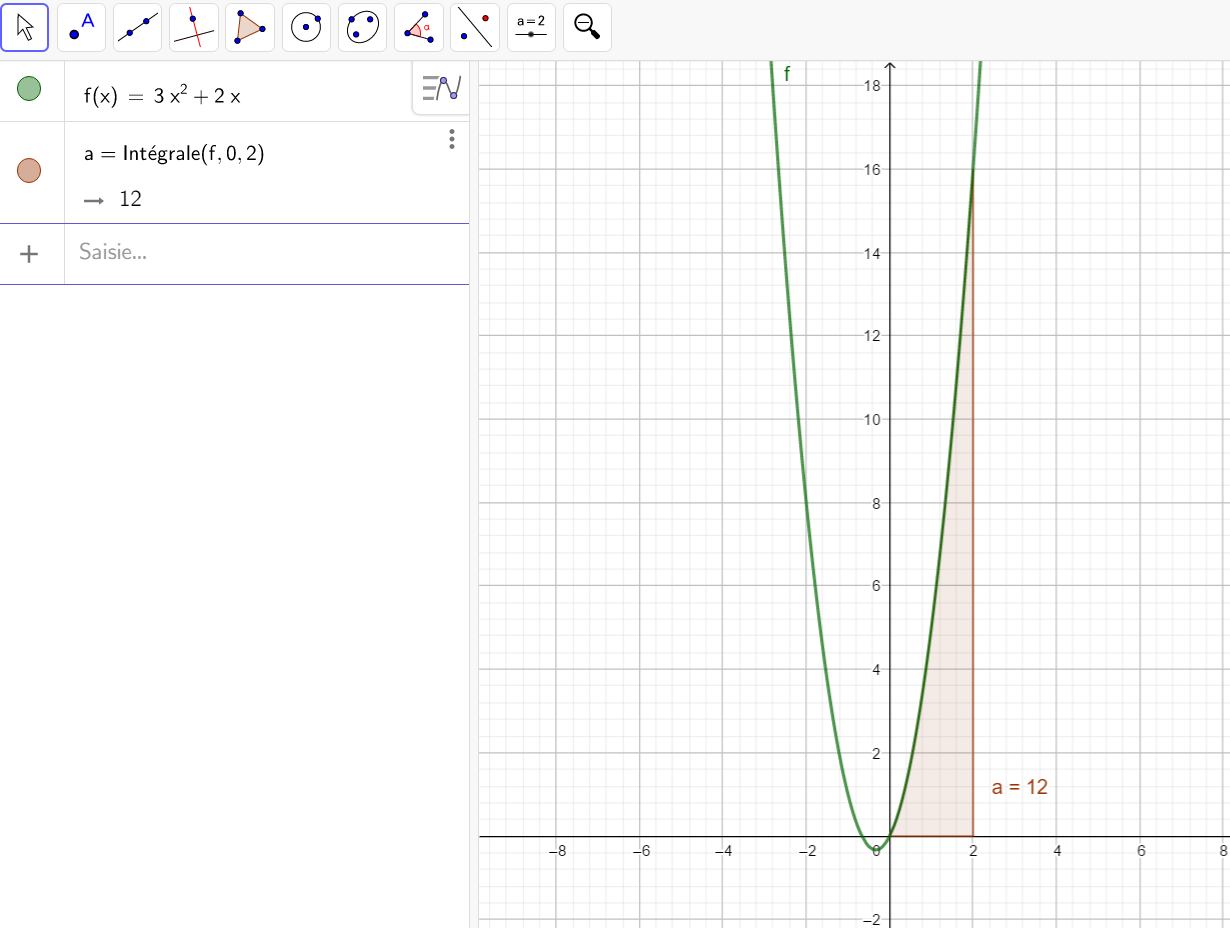
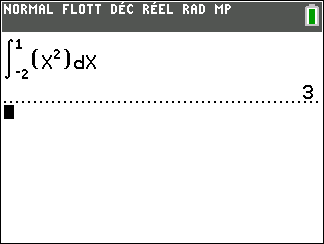
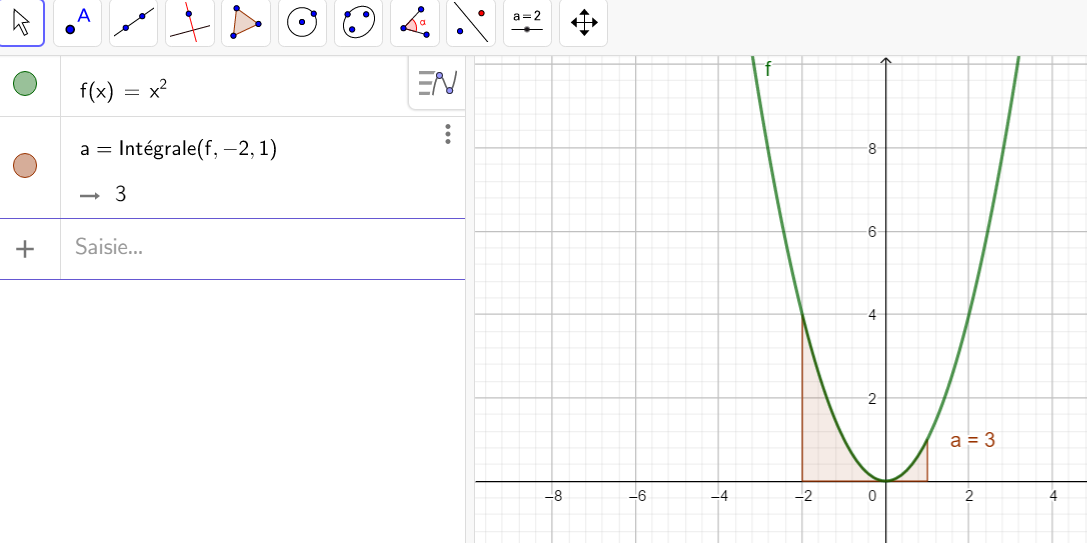
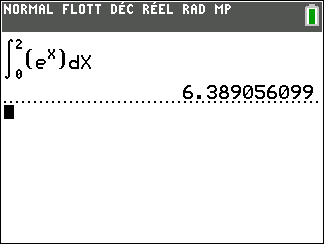
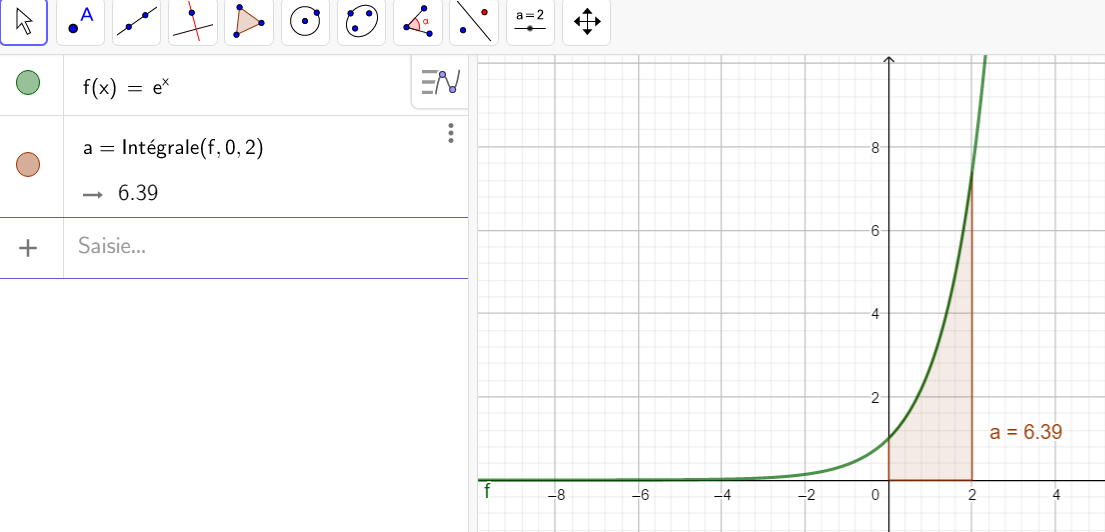
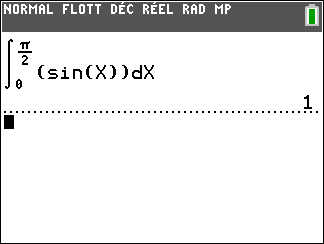
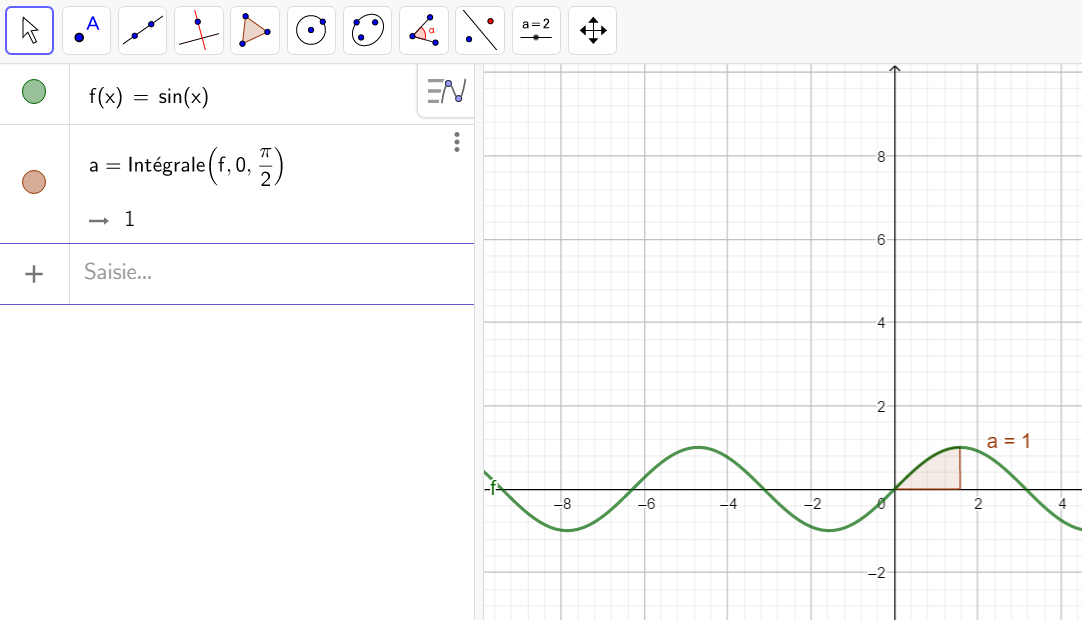
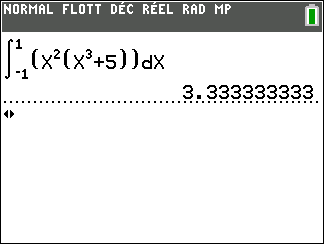
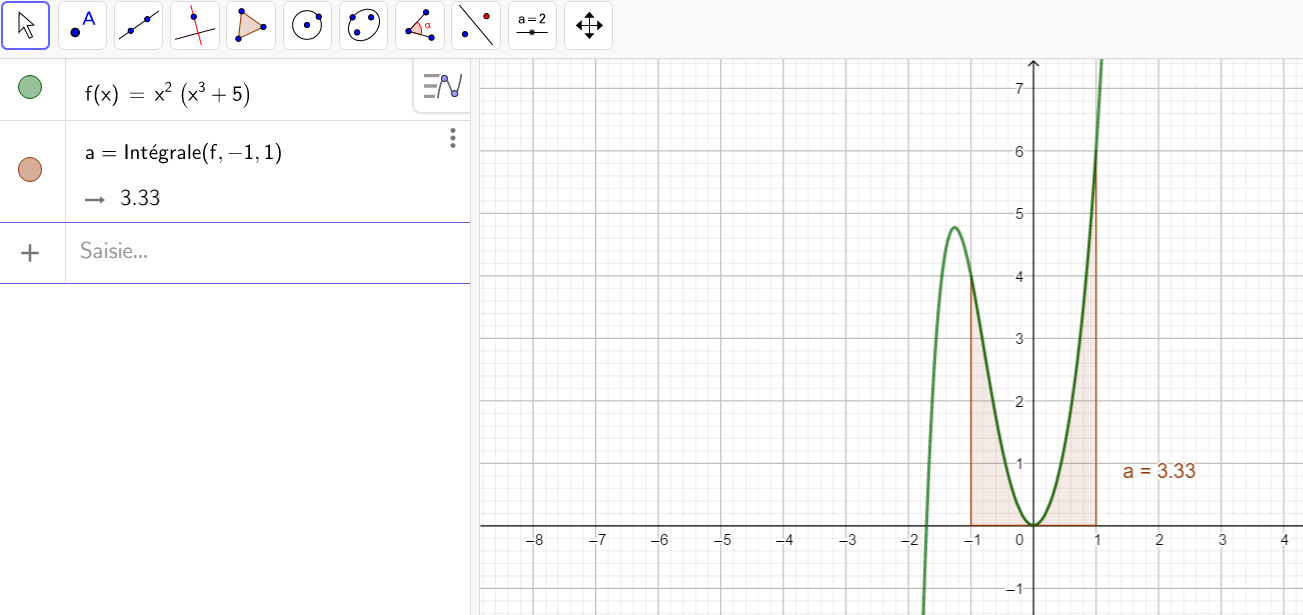
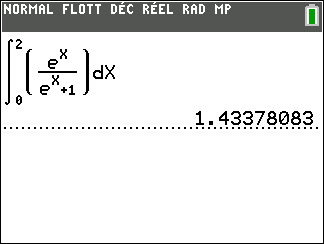
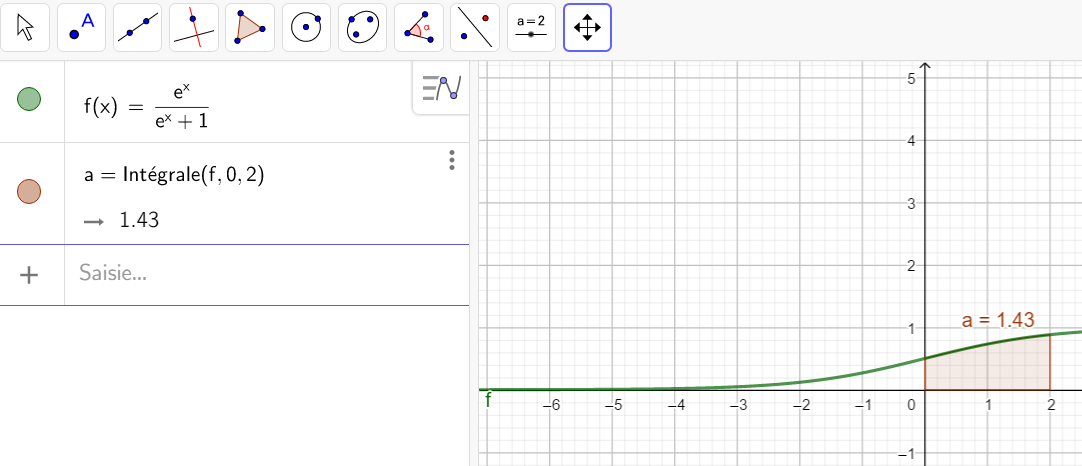
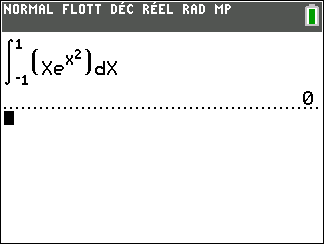
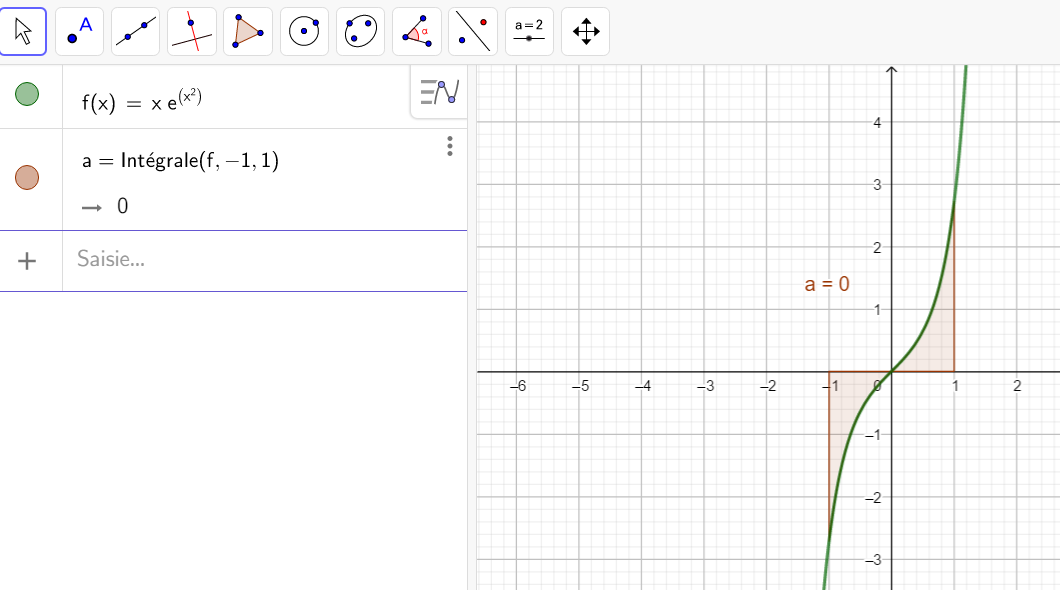
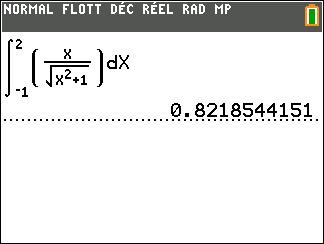
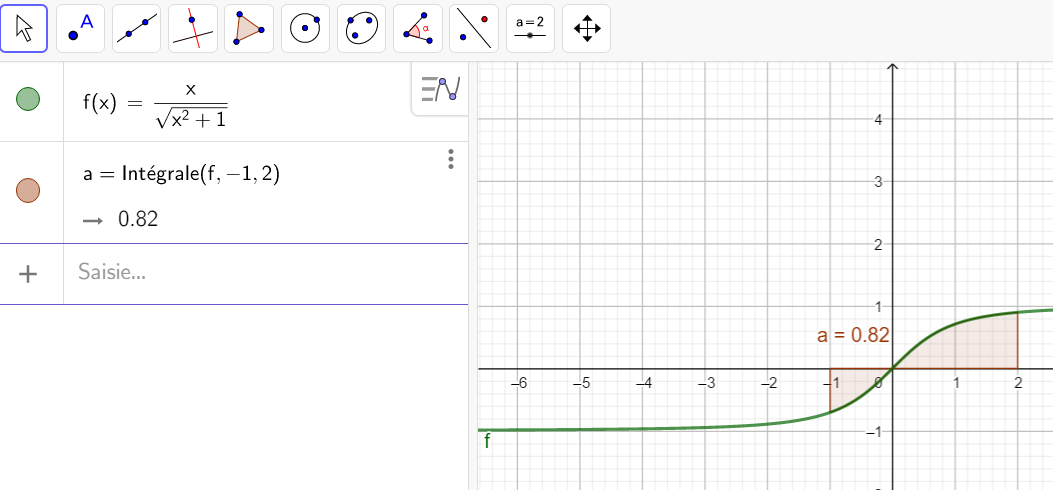
Calculer une intégrale avec Géogébra
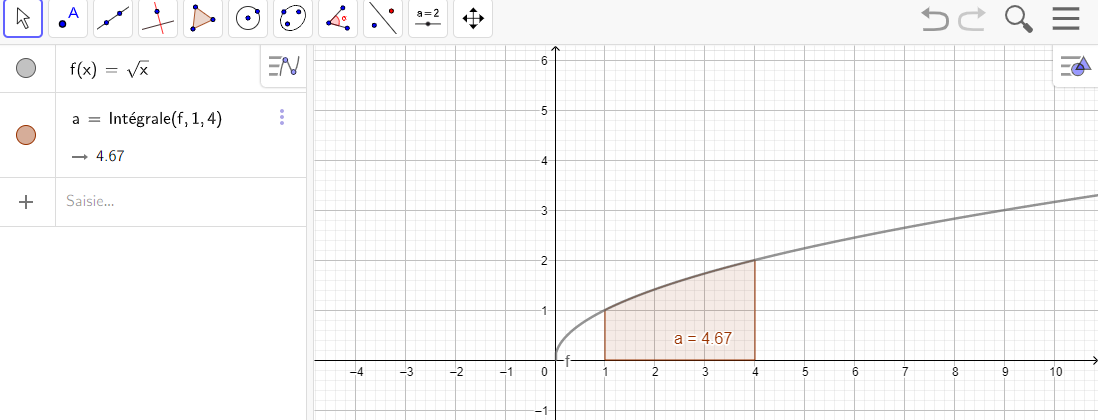
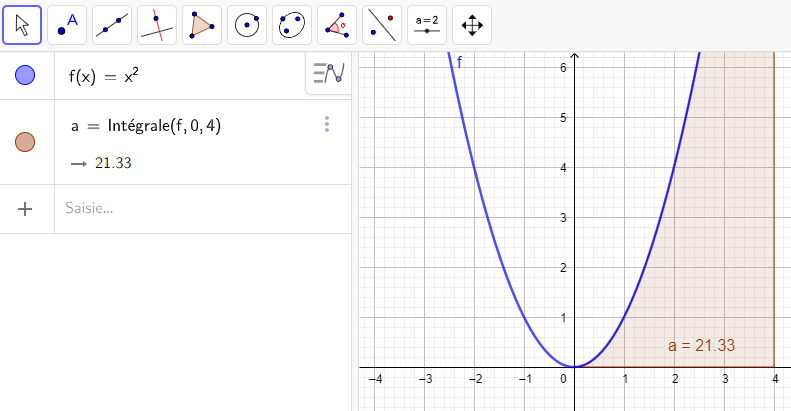
Après avoir saisi la fonction, par exemple f(x)=\sqrt{x}.
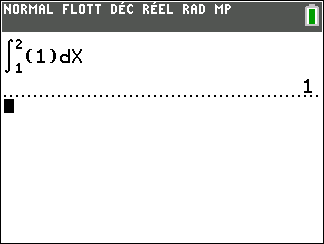
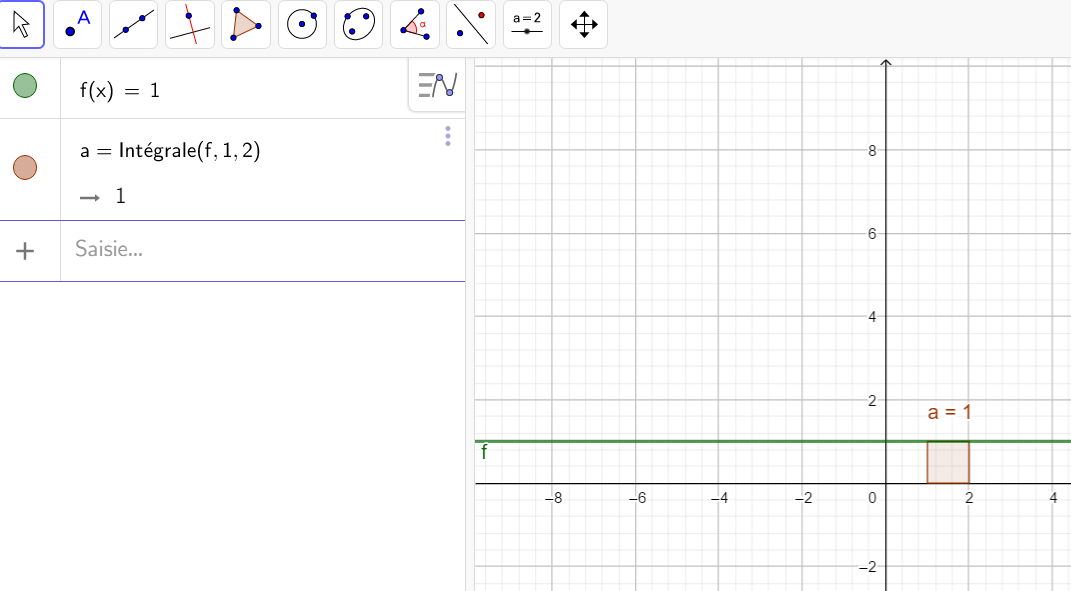
Il faut saisir en-dessous , dans la colonne Algèbre située à gauche de l’écran, intégrale(f,0,4).
La valeur de l’intégrale s’affiche dans la colonne Algèbre et l’aire correspondante apparaît en couleur dans le repère.
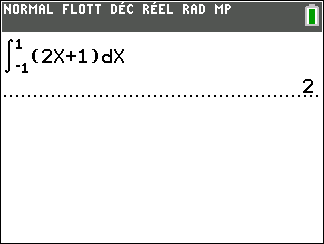
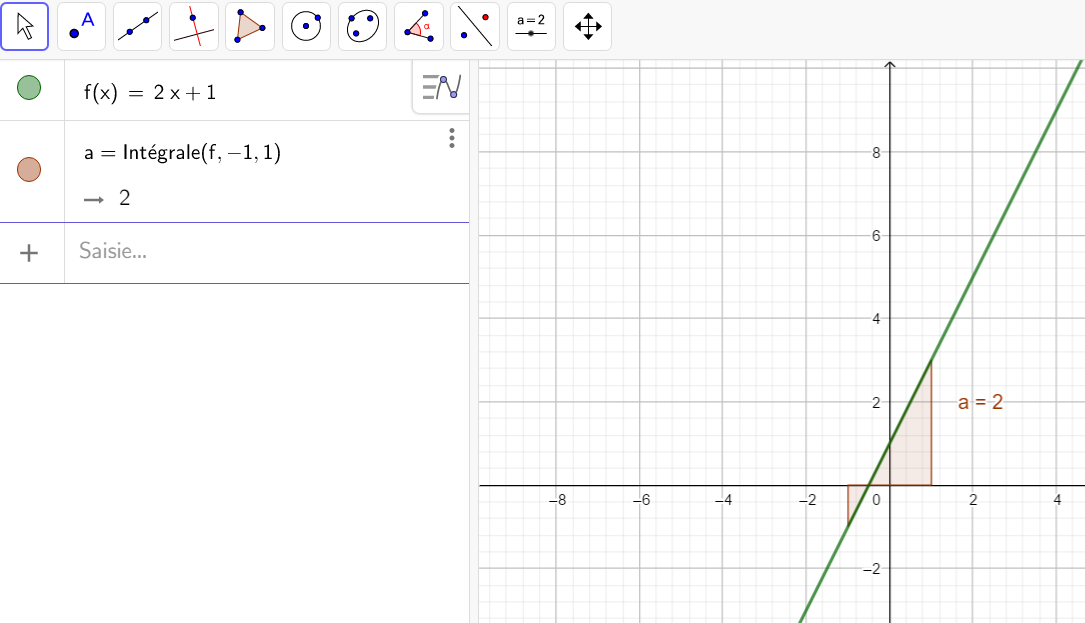
Exercice n°1
En utilisant, la page Géogébra ci_dessus, calculer les intégrales suivantes ( il n’est pas nécessaire de tout retaper, modifier juste ce qui doit l’être ). On a choisi des fonctions continues et positives sur leur intervalle d’intégration.
1.\int_1^4 \sqrt{x}\hspace{0.05cm}dx
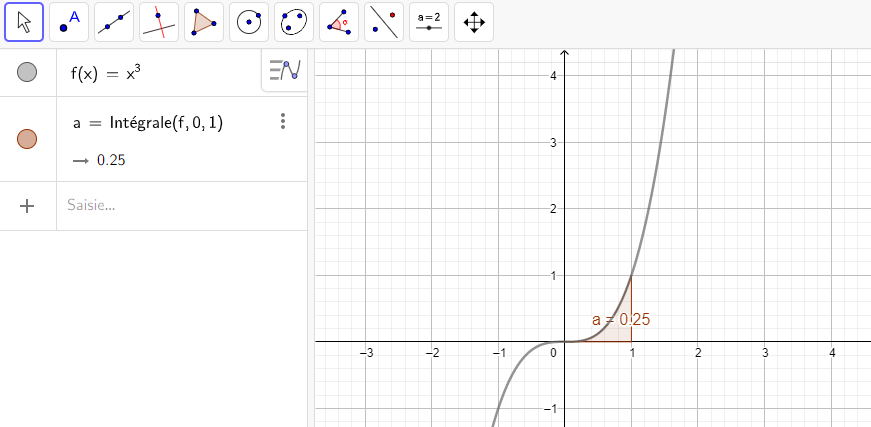
2.\int_0^1 x^3\hspace{0.05cm}dx
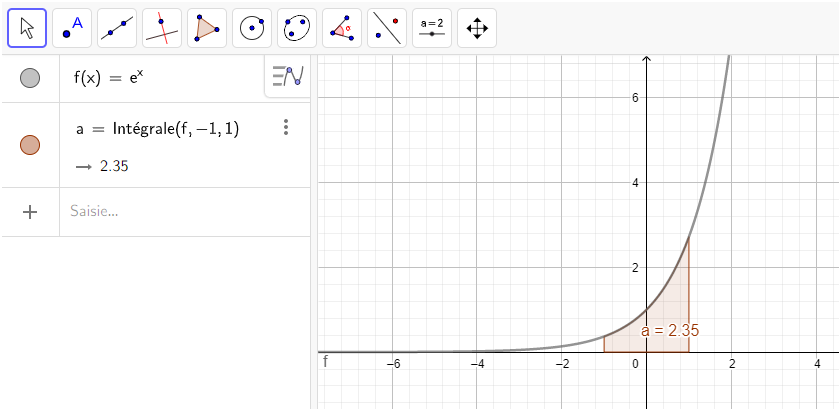
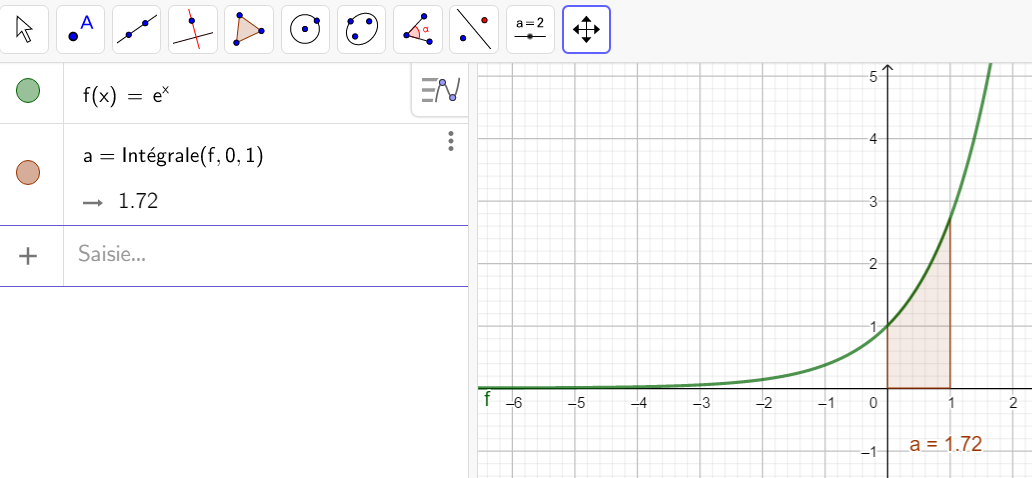
3.\int_{-1}^1 e^x\hspace{0.05cm}dx
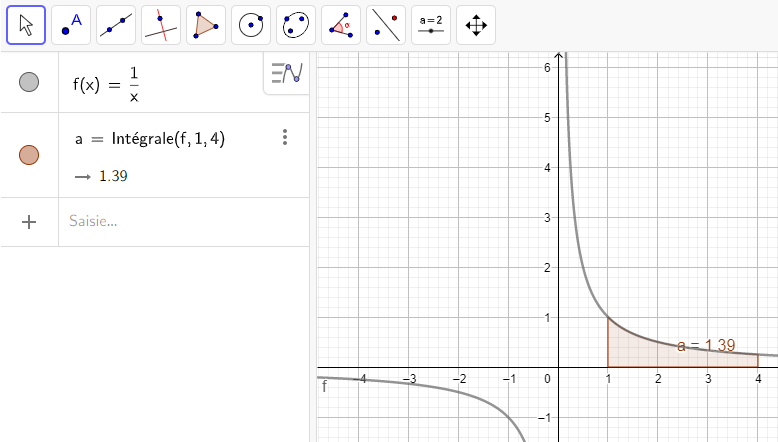
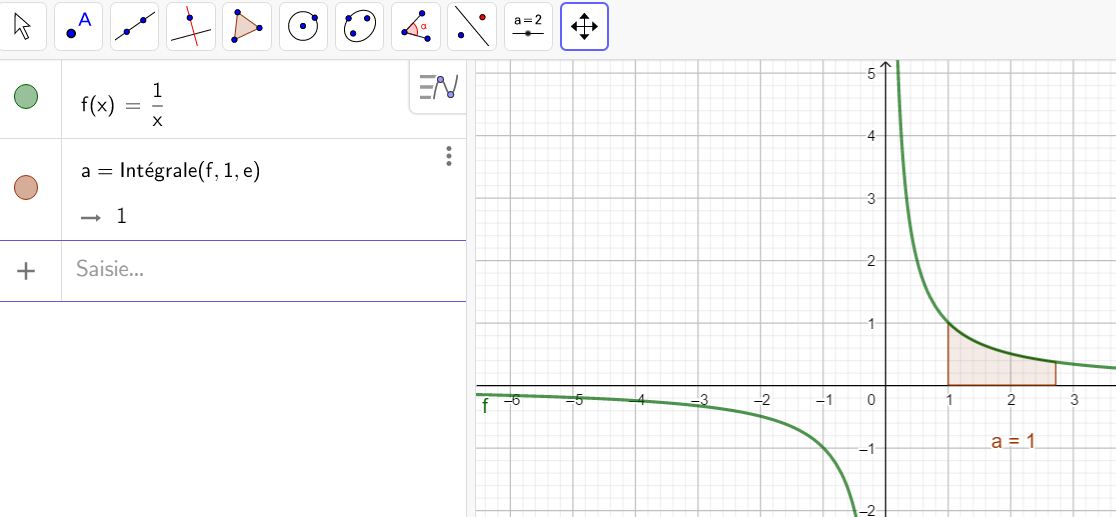
4.\int_1^4 \frac{1}{x}\hspace{0.05cm}dx
5.\int_{-2}^{1} x^2\hspace{0.05cm}dx
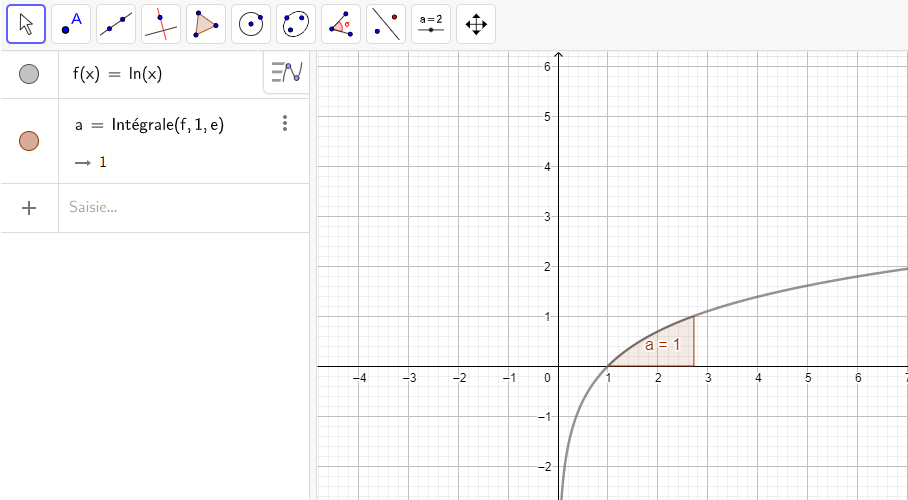
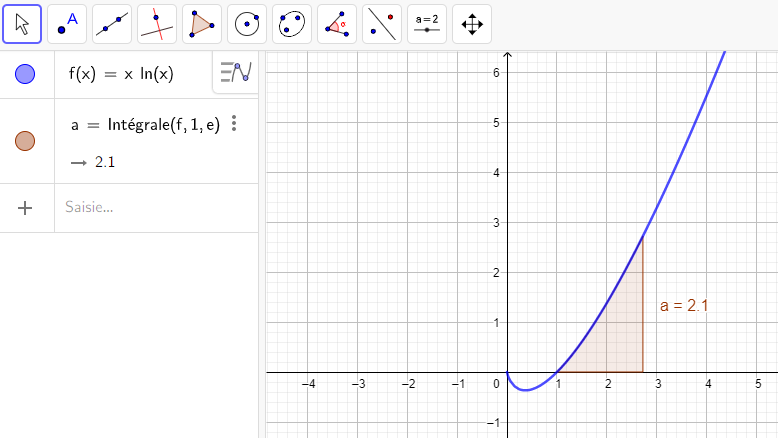
6.\int_1^e ln(x)\hspace{0.05cm}dx
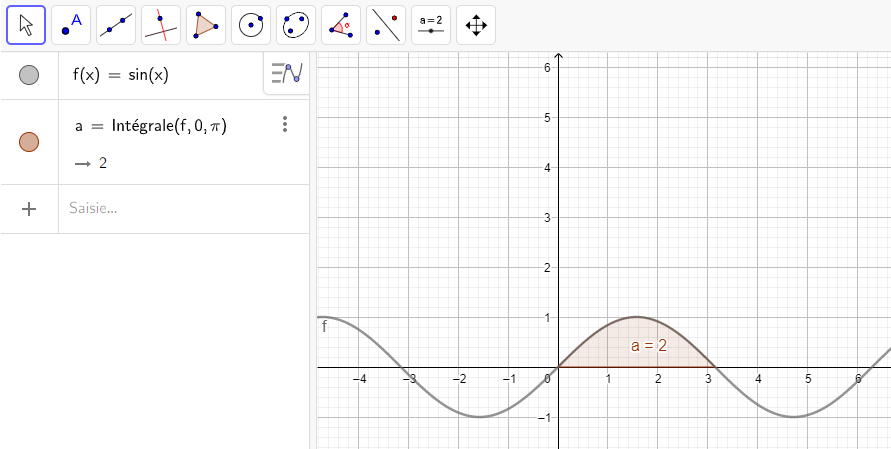
7.\int_{0}^{\pi} sin(x)\hspace{0.05cm}dx
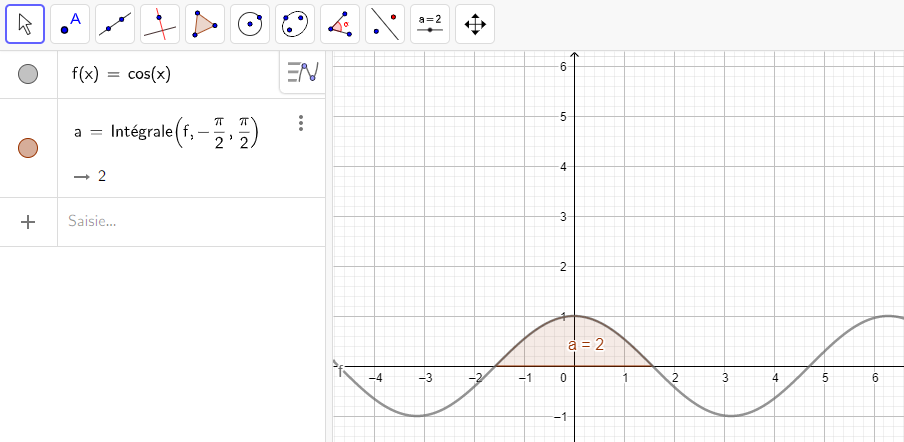
8.\int_{-\pi}^{\pi} cos(x)\hspace{0.05cm}dx
Intégrale d’une fonction continue
Théorème fondamental
Soit f une fonction continue sur un intervalle [a;b].
La fonction F_a définie sur [a;b] par F_a(x)=\int_a^x f(f)\hspace{0.05cm}dt est la primitive de f sur [a;b] qui s’annule en a.
C’est-à-dire que pout tout x de [a;b] , F_a'(x)=f(x).
Calcul de l’intégrale d’une fonction continue
Propriété
Soit f une fonction continue et positive sur un intervalle [a;b].
Si F est une primitive de f alors \int_a^b f(x)\hspace{0.05cm}dx=F(b)-F(a).
Propriété
Toute fonction continue sur un intervalle I admet des primitives sur I.
Définition
Soit f une fonction continue sur un intervalle I , F une une primitive de f et a et b deux réels de I. On appelle intégrale de a à b de f le réel noté \int_a^b f(x)\hspace{0.05cm}dx=[F(x)]_a^b=F(b)-F(a).
Exercice n°2
Calculer les intégrales suivantes en utilisant la définition ci-dessus.
Exercice n°3
Calculer les intégrales suivantes en utilisant la définition ci-dessus.
Propriétés et intégration par parties
Propriétés
Soient f et g deux fonctions continues sur un intervalle I.
a,b,c sont trois réels de l’intervalle I et k est une constante réelle.
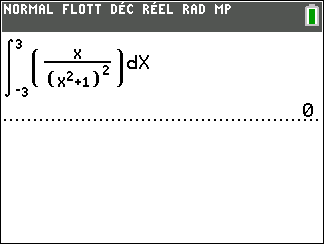
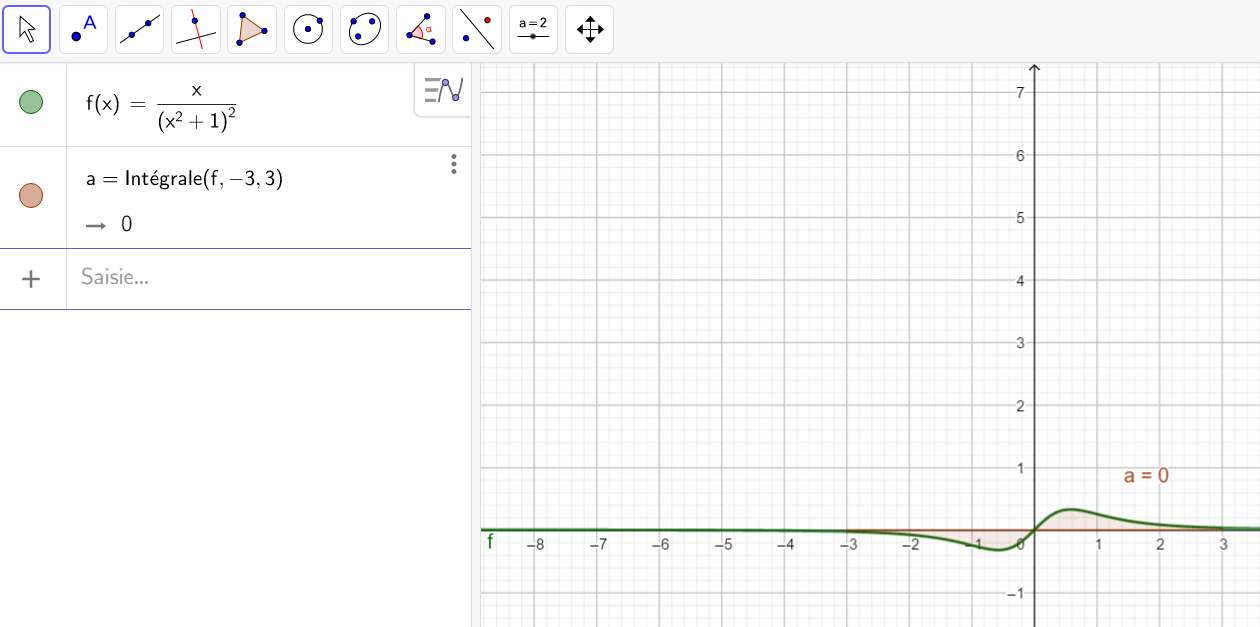
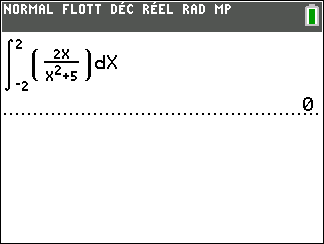
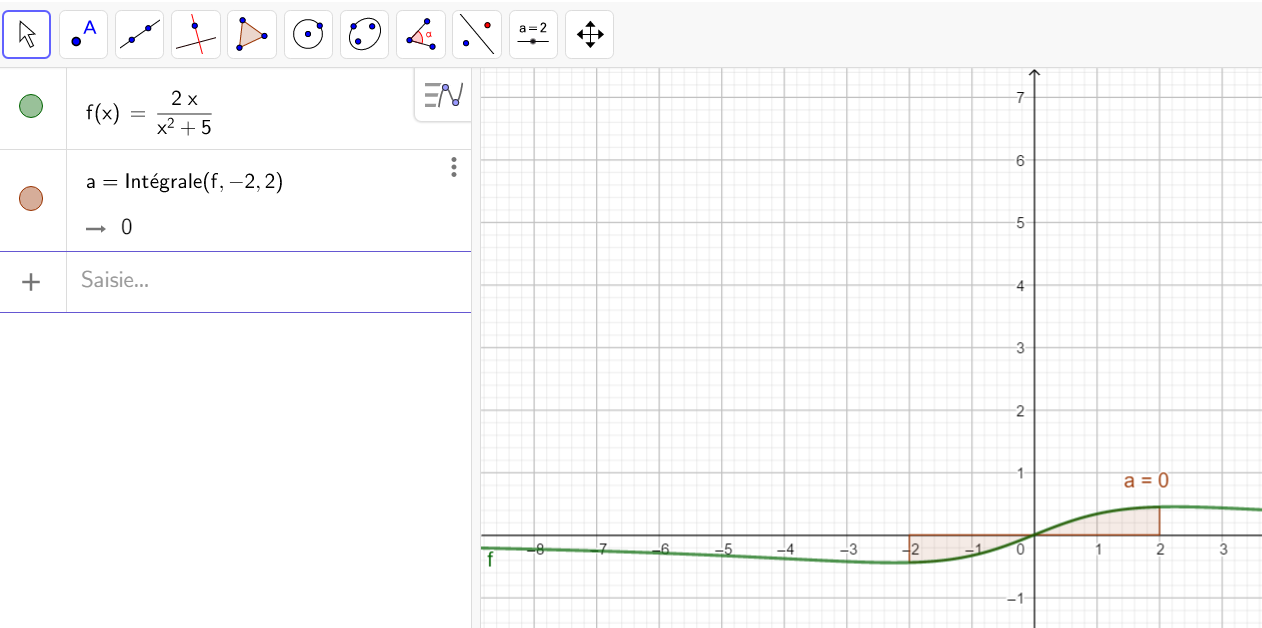
- \int_{a}^a f(x)\hspace{0.05cm}dx=0
2. \int_{b}^a f(x)\hspace{0.05cm}dx=-\int_{a}^b f(x)\hspace{0.05cm}dx
3. \int_{a}^b kf(x)\hspace{0.05cm}dx=k\int_{a}^b f(x)\hspace{0.05cm}dx
4. \int_{a}^b (f(x)+g(x))\hspace{0.05cm}dx=\int_{a}^b f(x)\hspace{0.05cm}dx +\int_{a}^b g(x)\hspace{0.05cm}dx
5. \int_{a}^b f(x)\hspace{0.05cm}dx+\int_{b}^c f(x)\hspace{0.05cm}dx =\int_{a}^c f(x)\hspace{0.05cm}dx
6. Si pour tout x de [a;b], f(x)\geq 0 alors \int_{a}^b f(x)\hspace{0.05cm}dx\geq 0
7. Si pour tout x de [a;b], f(x)\geq g(x) alors \int_{a}^b f(x)\hspace{0.05cm}dx\geq \int_{a}^b g(x)\hspace{0.05cm}dx
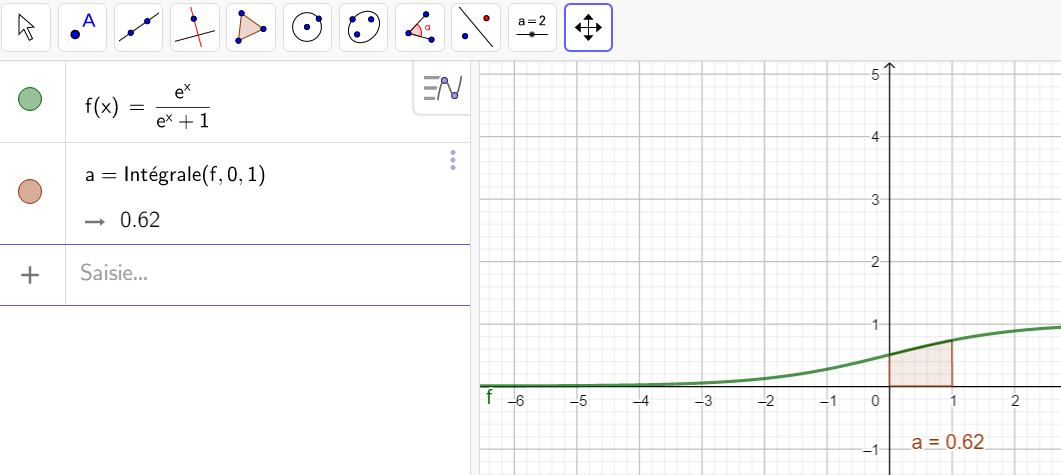
Exercice n°4
Soit I=\int_{0}^1 \frac{e^x}{e^x+1}\hspace{0.05cm}dx et J=\int_{0}^1 \frac{1}{e^x+1}\hspace{0.05cm}dx
- Utiliser la propriété n°4 et calculer ensuite la valeur de I+J
2. Calculer la valeur de I
3. Déduire des questions précédentes la valeur de J.
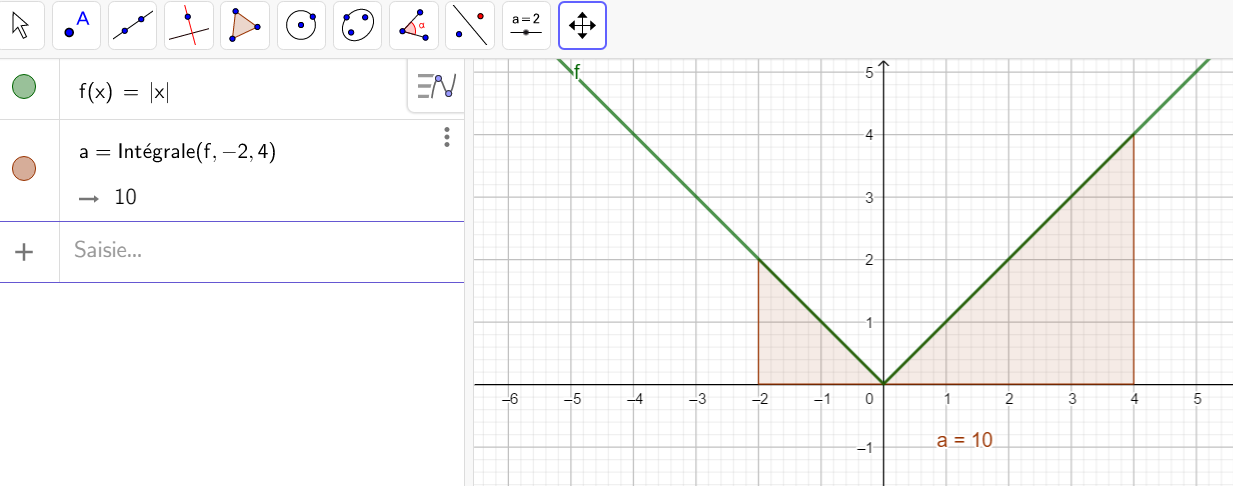
Exercice n°5
En utilisant la relation de Chasles, calculer \int_{-2}^4 |x|\hspace{0.05cm}dx
Exercice n°6
- Donner un encadrement de ln(x) sur l’intervalle [1;e]
2. En utilisant la propriété n°7, en déduire que 0\leq \int_{1}^e x^2ln(x)\hspace{0.05cm}dx\leq \frac{e^3-1}{3} .
Intégration par parties
Soient u et v deux fonctions dérivables sur un intervalle I et dont les dérivées u’ et v’ sont continues sur I .
a,b sont deux réels de l’intervalle I.
\int_{b}^a u(x)v'(x)\hspace{0.05cm}dx=[u(x)v(x)]_{a}^b-\int_{a}^b u'(x)v(x)\hspace{0.05cm}dx
Exercice n°7
Calculer les intégrales suivantes à l’aide d’une intégration par parties..
1.\int_{1}^e xln(x)\hspace{0.05cm}dx
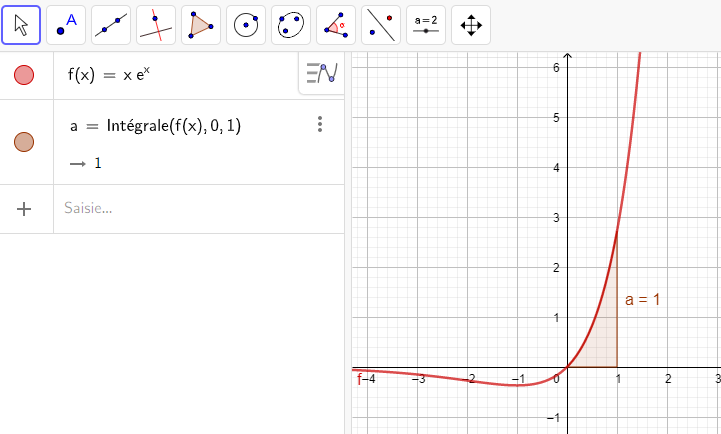
2.\int_{0}^1xe^x \hspace{0.05cm}dx
3.\int_{0}^{\frac{\pi} {3}}(x-1)cos(x) \hspace{0.05cm}dx
4.\int_{1}^e ln(x)\hspace{0.05cm}dx
Applications du calcul intégral
Calculs d’aires
Cas n°1 : f est positive sur [a;b].
L’aire limitée par x=a , x=b , C_f et l’axe des abscisses est \int_{a}^b f(x)\hspace{0.05cm}dx
Exemple n°1 :
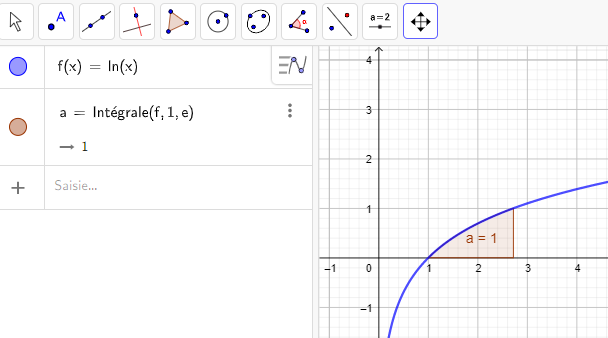
L’aire limitée par x=1 , x=e , C_f et l’axe des abscisses est \int_{1}^e f(x)\hspace{0.05cm}dx=1
Cas n°2 : f est négative sur [a;b].
L’aire limitée par x=a , x=b , C_f et l’axe des abscisses est -\int_{a}^b f(x)\hspace{0.05cm}dx
Exemple n°2 :
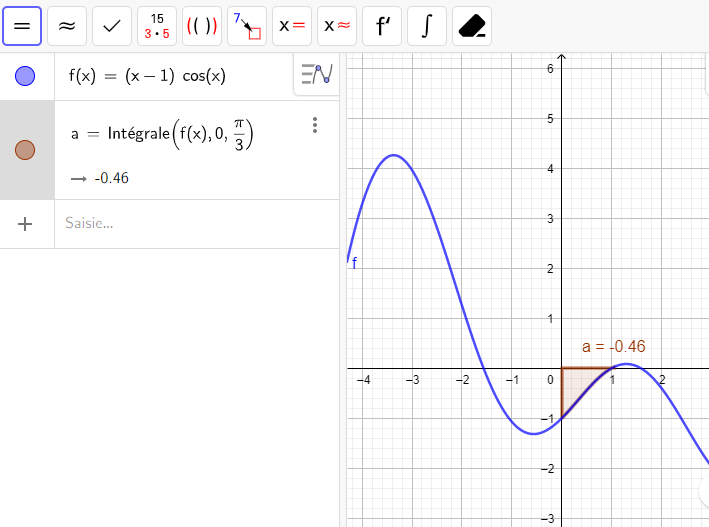
L’aire limitée par x=0 , x=\frac{\pi}{3} , C_f et l’axe des abscisses est -\int_{0}^{\frac{\pi}{3}} f(x)\hspace{0.05cm}dx=-(-0.46)
Cas n°3: f change de signe sur [a;b].
On utilise la relation de Chasles et ce qu’on a vu dans les cas 1 et 2 pour calculer l’aire limitée par x=a , x=b , C_f et l’axe des abscisses.
Exemple n°3 :
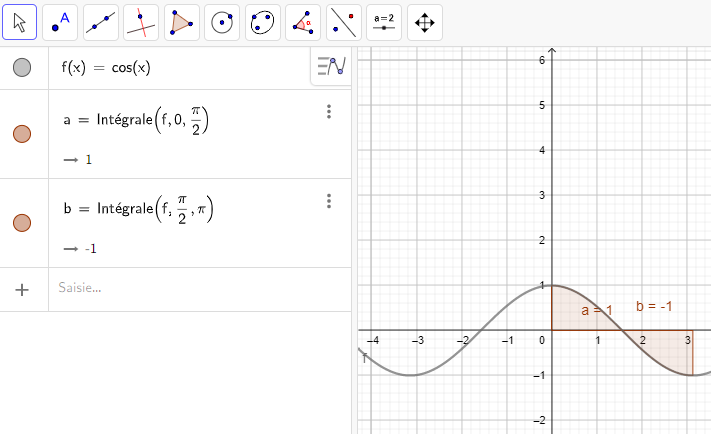
L’aire limitée par x=0 , x=\pi , C_f et l’axe des abscisses est \int_{0}^{\frac{\pi}{2}} f(x)\hspace{0.05cm}dx–\int_{\frac{\pi}{2}}^{\pi} f(x)\hspace{0.05cm}dx=1-(-1)=2
Exercice n°8
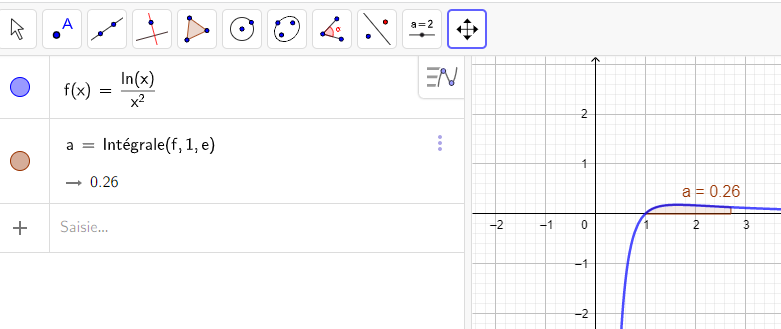
Soit f une fonction définie sur ]0;+\infty[ par f(x)=\frac{ln(x)}{x^2}.
Calculer, en unités d’aire, l’aire du domaine compris entre la courbe C_f , l’axe des abscisses et les droites d’équations respectives x=1 et x=e.
On utilisera une intégration par parties.
Exercice n°9
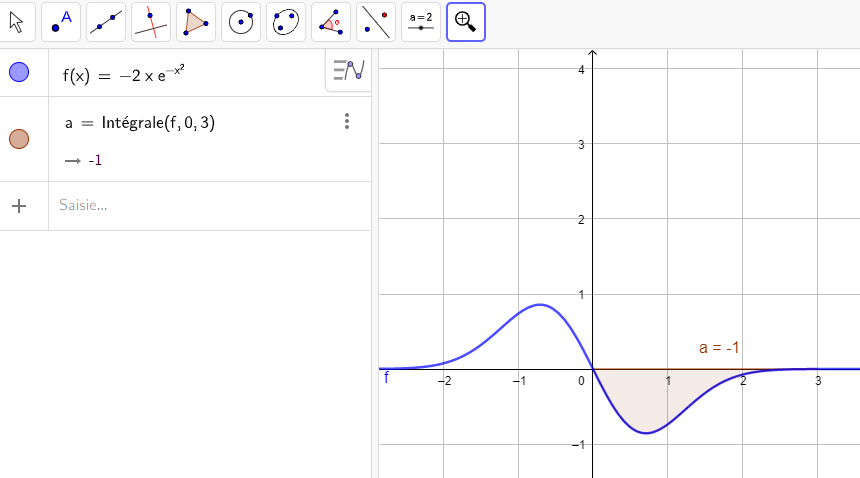
Soit f une fonction définie sur \mathbf{R} par f(x)=-2xe^{-x^2}.
Calculer, en unités d’aire, l’aire du domaine compris entre la courbe C_f , l’axe des abscisses et les droites d’équations respectives x=0 et x=3.
Propriété
Soient f et g deux fonctions continues sur un intervalle I telles que f(x)\leq g(x)
Soient deux réels a et b de l’intervalle I tels que a<b.
L’aire ( en unités d’aire) de la partie du plan limitée par x=a , x=b , C_f et C_g est égale à :
\int_{a}^b (g(x)-f(x))\hspace{0.05cm}dx
Exercice n°10
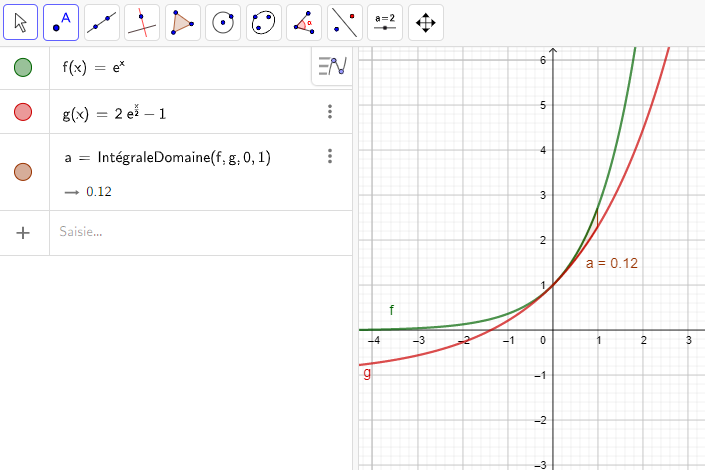
Soient f et g les fonctions définies sur \mathbf{R} par
f(x)=e^x et g(x)=2e^{\frac{x}{2}}-1.
On admet que f(x)\geq g(x) Calculer, en unité d’aire, l’aire du domaine compris entre les courbes ) Calculer, en unité d’aire, l’aire du domaine compris entre les courbes C_f et C_g et les droites d’équations respectives x=0 et x=1.
Valeur moyenne d’une fonction
Propriété
Soit f une fonction continue sur un intervalle [a;b].
On appelle valeur moyenne de f sur [a;b] le réel suivant :
\frac{1}{b-a}\int_{a}^b f(x)\hspace{0.05cm}dx
Exercice n°11
Calculer la valeur moyenne de f sur l’intervalle proposé
1.f(x)=x^2 sur l’intervalle [0;4]
2.f(x)=\frac{1}{x} sur l’intervalle [1;e]
3.f(x)=e^x sur l’intervalle [0;1].
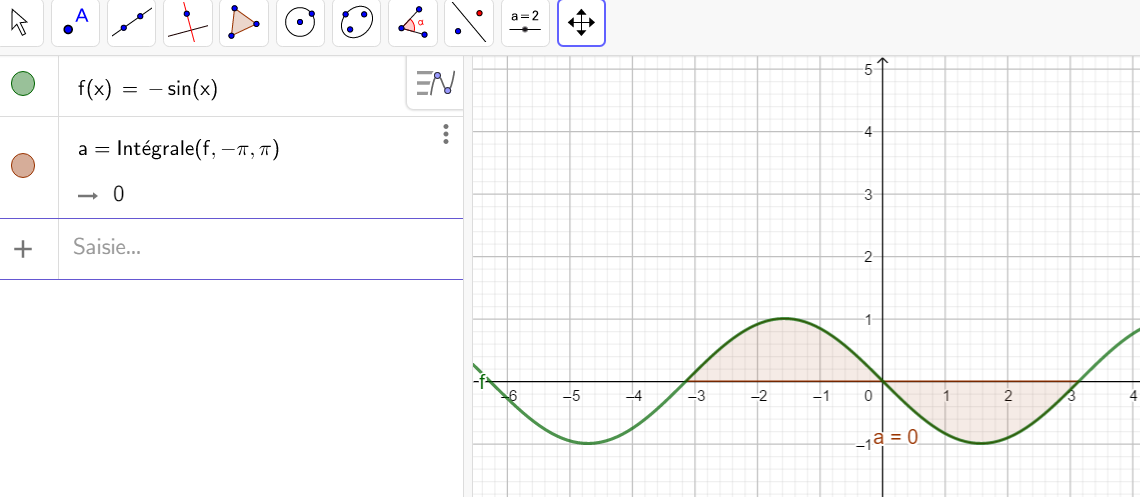
4.f(x)=-sin(x) sur l’intervalle [-\pi;\pi].