Exercice n°2 : centres étrangers 11 Mai 2022
Partie A
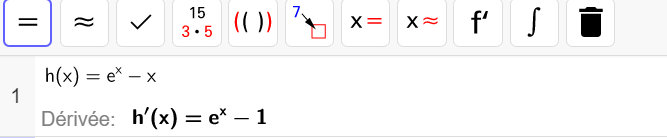
Soit h la fonction définie sur \mathbf{R}par
h(x)=e^x-x
1. Déterminer les limites de h en -\infty et +\infty.
2. Étudier les variations de h et dresser son tableau de variation.
3. En déduire que :
si a et b sont deux réels tels que 0<a<b alors h(a)-h(b)<0.
Partie B
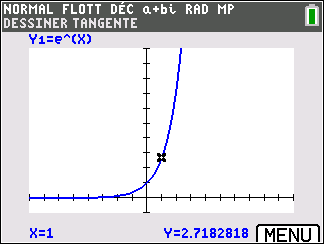
Soit f la fonction définie sur \mathbf{R}par
f(x)=e^x
On note C_f sa courbe représentative dans un repère orthomormé..
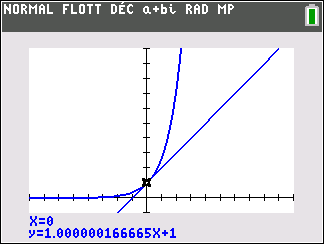
1. Déterminer une équation de la tangente T à C_f au point d’abscisse 0.
Dans la suite de l’exercice on s’intéresse à l’écart entre T et C_f au voisinage de 0.
Cet écart est défini comme la différence des ordonnées des points de T et C_f de même abscisse.
On s’intéresse aux points d’abscisse \frac{1}{n}, avec n entier naturel non nul.
On considère alors la suite (u_n) définie pour tout entier naturel non nul n par :
u_n=exp(\frac{1}{n})-\frac{1}{n}-1.
2. Déterminer la limite de la suite (u_n).
3. a. Démontrer que, pour tout entier naturel non nul n,
u_{n+1}-u_n=h(\frac{1}{n+1})-h(\frac{1}{n}).
où h est la fonction définie à la partie A.
b. En déduire le sens de variation de la suite (u_n).
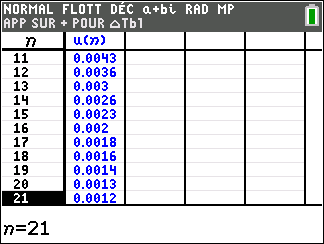
4. Le tableau ci-dessous donne des valeurs approchées à 10^{-9} des premiers termes de la suite (u_n).
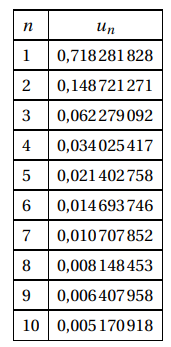
Donner la plus petite valeur de l’entier naturel n pour laquelle l’écart entre T et C_f semble être inférieur à 10^{-2}..