Résolvons dans \mathbf{R}, l’inéquation suivante 2x^{2}-5x+1 >1
L’inéquation à résoudre 2x^{2}-5x+1 >1 est du 2nd degré . Dans 2x^{2}-5x+1 le plus grand exposant de x est 2.
La méthode proposée concerne les inéquations du second degré.
2x^{2}-5x+1 >1
1.Je fais tout passer à gauche, zéro apparaît à droite.
le 1 à droite n’est pas à sa place, j’enlève 1 de chaque côté.
2x^{2}-5x+1-1 >0
2x^{2}-5x >0
2. Je factorise le membre de gauche.
a. Il y a un facteur commun.
2x^{2}= {x}\times{2x}
5x ={x}\times{5}
x(2x-5) > 0
3. J’écris la phrase d’introduction.
Je cherche pour quelles valeurs de x, le produit x(2x-5) est de signe(+) .
4. Je prépare mon tableau de signes.
Je résous x=0
Je résous 2x-5=0\\2x=5\\x=\frac{5}{2}
Je place les valeurs 0 et \frac{5}{2} sur la première ligne du tableau en les rangeant dans le bon ordre. Je place les zéros sur les lignes en-dessous.
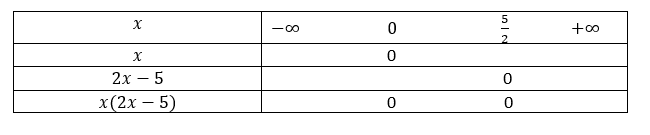
Je remplis ce tableau avec des signes (-), (+) , des zéros et parfois des doubles barres quand il y a des valeurs interdites.
On utilise le résultat du cours suivant :

Sur la ligne du facteur x, comme a=1 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).
Sur la ligne du facteur (2x-5), comme a=2 , on commence par le signe (-) jusqu’au zéro et on complète avec des (+).
Pour compléter la ligne du produit x(2x-5), j’applique la règle des signes pour le produit.
plus par plus : plus.
plus par moins : moins.
moins par plus : moins.
moins par moins : plus.
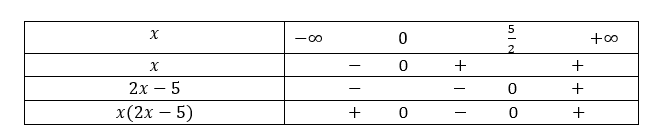
5. Je réponds à la phrase d’introduction.
Le produit x(2x-5) est de signe(+) pour les première et troisième colonnes qui correspondent aux valeurs de x comprises entre -\infty et 0 puis entre \frac{5}{2} et +\infty.
Je ne prends pas les valeurs 0 et \frac{5}{2} car le produit ne peut pas être nul. Donc j’ouvre les crochets en 0 et \frac{5}{2}, ce qui signifie que les crochets sont tournés vers l’extérieur de l’intervalle.
S=]-\infty;0[\cup]\frac{5}{2};+\infty[



