logo

TS. bac 2022 probabilités exercice n°1 ( Polynésie 4 mai 2022 sujet 1)

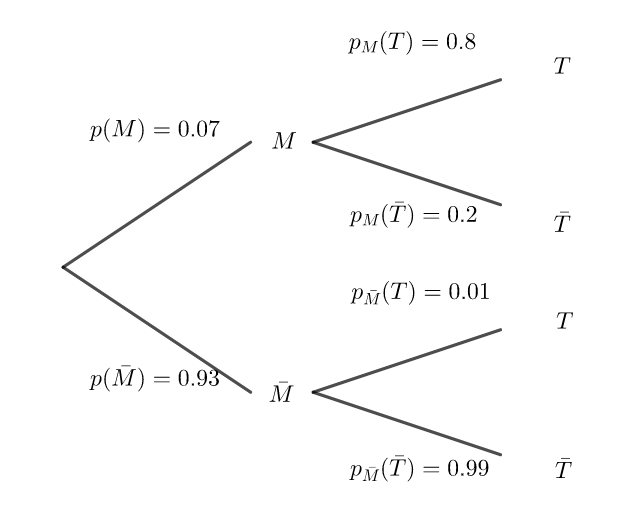
Selon les autorités sanitaires d’un pays, 7% des habitants sont affectés par une certaine maladie.
Dans ce pays, un test est mis au point pour détecter cette maladie. Ce test a les caractéristiques suivantes :
• Pour les individus malades, le test donne un résultat négatif dans 20% des cas;
• Pour les individus sains, le test donne un résultat positif dans 1% des cas.
Une personne est choisie au hasard dans la population et testée.
On considère les évènements suivants :
• M « la personne est malade »;
• T « le test est positif ».
1. Calculer la probabilité de l’évènement M\cap T. On pourra s’appuyer sur un arbre pondéré.

correction arbre pondéré
correction p(M\cap T)

2. Démontrer que la probabilité que le test de la personne choisie au hasard soit positif vaut 0.0653.

correction

3. Dans un contexte de dépistage de la maladie, est-il plus pertinent de connaître P_M(T) ou P_T(M)?

correction

4. On considère dans cette question que la personne choisie au hasard a eu un test positif.
Quelle est la probabilité qu’elle soit malade ?

On arrondira le résultat à 10^{-2} près.

correction

5. On choisit des personnes au hasard dans la population. La taille de la population de
ce pays permet d’assimiler ce prélèvement à un tirage avec remise.
On note X la variable aléatoire qui donne le nombre d’individus ayant un test positif
parmi les 10 personnes.
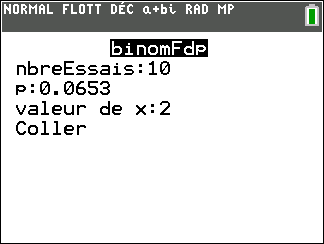
a. Préciser la nature et les paramètres de la loi de probabilité suivie par X.

correction

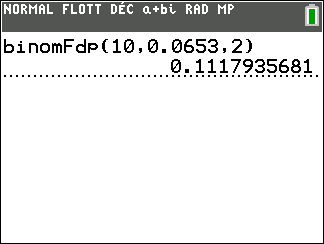
b. Déterminer la probabilité pour qu’exactement deux personnes aient un test positif.

On arrondira le résultat à 10^{-2} près.

correction

6. Déterminer le nombre minimum de personnes à tester dans ce pays pour que la probabilité qu’au moins l’une d’entre elle ait un test positif, soit supérieur à 99%.

correction

©2020 – Math’O karé SAS

Conseil : il est parfois utile de reformuler les phrases pour se ramener au plus près des définitions du cours.

Selon les autorités sanitaires d’un pays, 7 % des habitants sont affectés par une certaine maladie, donc p(M)=0.07.

Pour les individus malades, le test donne un résultat négatif dans 20% des cas

On peut aussi écrire : sachant que la personne est malade, la probabilité qu’elle ait un test négatif est 0.2.

donc p_M(\bar{T})=0.2

Pour les individus sains, le test donne un résultat positif dans 1% des cas

On peut aussi écrire : sachant que la personne n’est pas malade, la probabilité qu’elle ait un test positif est 0.01.

donc p_{\bar{M}}(T)=0.01.

On reporte les probabilités trouvées sur les branches correspondantes de l’arbre ci-dessous.

Pour les branches sans probabilités, on utilise la propriété suivante : la somme des probabilités sur les branches issues d’un même noeud est égale à 1.

Par exemple la somme des probabilités sur les branches primaires est égale à 1 donc  p(M)+p(\bar{M})=1

0.07+p(\bar{M})=1

p(\bar{M})=1-0.07

p(\bar{M})=0.93

Par exemple la somme des probabilités sur les branches secondaires issues de l’évènement M est égale à 1 donc p_M(T)+p_M(\bar T)=1

p_M(T)+0.2=1

p_M(T)=1-0.2

p_M(T)=0.8

Par exemple la somme des probabilités sur les branches secondaires issues de l’évènement \bar M est égale à 1 donc p_{\bar M} (T)+p_{\bar M}(\bar T)=1

0.01+p_{\bar M}(\bar T)=1

p_{\bar M}(\bar T)=1-0.01

p_{\bar M}(\bar T)=0.99

Calculer p(M\cap T) revient à calculer la probabilité du chemin qui passe par M et T en multipliant les probabilités sur les branches, ce qui revient à appliquer la formule du cours p(M\cap T)=p(M)\times p_M(T).

p(M\cap T)=0.07\times 0.8=0.056.

On veut démontrer que la probabilité que le test de la personne choisie au hasard soit positif vaut 0.0673.

On veut calculer p(T), il faut ajouter les probabilités de tous les chemins qui mènent à T. Ici il y en a deux.

Cela revient à appliquer la formule des probabilités totales :

p(T)=p(M\cap T)+p(\bar M\cap T)

On a vu précédemment que p(M\cap T)=0.056

\hspace{0.85cm}=0.056+p(\bar M)\times p_{\bar M}(T)

\hspace{0.85cm}=0.056+0.93\times 0.01

\hspace{0.85cm}=0.056+0.0093

\hspace{0.85cm}=0.0653

p_M(T) est la probabilité d’avoir un test positif sachant qu’on est malade

p_T(M) est la probabilité d’être malade sachant que le test est positif.

Pour dépister une maladie, mieux vaut calculer la probabilité d’être malade sachant que le test est positif c’est-à-dire p_T(M).

La personne choisie au hasard a eu un test positif. Quelle est la probabilité qu’elle soit malade ? 

On reformule : sachant que la personne a eu un test positif, quelle est la probabilité qu’elle soit malade?

La condition est la personne a eu un test positif.

Pour calculer p_{T}(M), on ne peut pas utiliser l’arbre car pour l’arbre la condition est M ou \bar M. On applique donc la formule du cours.

p_{T}(M)=\frac{p(T\cap M)}{p(T)}

p_{T}(M)=\frac{0.056}{0.0653}

 

p_{T}(M)=\frac{1}{12}\times \frac{3}{1}

 

p_{T}(M)=0.86

Le tirage étant assimilé à un tirage avec remise, on a une indépendance des 10 tirages, le succès étant
défini par le test positif, on peut assimiler cette variable aléatoire à une loi de Bernoulli de paramètre
n=10 et p=0.0653.

Pour calculer p(X=2), on utilise la calculatrice TI 83 Premium :

Au clavier

A l’écran

Appuyer sur la touche 2nde puis la touche var. Dans le menu déroulant, on sélectionne la ligne B:binomFdP 

On valide avec entrer

Sur la ligne nbreEssais on saisit le nombre total d’épreuves c’est-à-dire n.

Sur la ligne p on saisit la probabilité du succès.

Sur la ligne valeur de x on saisit le nombre de succès choisi.

 

On appuie sur la touche entrer deux fois

On rédige :

p(X=2)=\binom{10}{2}\times 0.0653^2\times(1-0.0653)^{10-2}\approx 0.11.

 

 

On veut déterminer le nombre minimum de personnes à tester dans ce pays pour que la probabilité qu’au moins l’une d’entre elles ait un test positif, soit supérieur à 99%.

On note n l’inconnue c’est-à-dire le nombre minimum de personnes à tester dans ce pays pour que la probabilité qu’au moins l’une d’entre elles ait un test positif, soit supérieur à 99%.

On met le problème en inéquation :

p(X \geq 1)>0.99

Le contraire de X \geq 1 est X =0. On peut donc résoudre 

1-p(X=0)>0.99

 

-p(X=0)>0.99-1

 

-p(X=0)>-0.01

Attention, on divise par -1, le sens de l’inégalité change.

p(X=0)<0.01

Comme p(X=0)=(1-0.0653)^{n}, on va résoudre 

(1-0.0653)^{n}<0.01

 

0.9347^{n}<0.01

 

0.9347^{n}<0.01

 

0.9347^{n}<0.01

La fonction ln est croissante, nombres et images varient dans le même sens.

ln(0.9347^{n})<ln(0.01)

 

nln(0.9347)<ln(0.01)

On divise par ln(0.9347) qui est négatif donc le sens de l’inégalité change.

n>\frac{ln(0.01)}{ln(0.9347)}

 

n>68.2

Il faut donc tester au minimum 69 personnes  pour que la probabilité qu’au moins l’une d’entre elles ait un test positif, soit supérieur à 99%.

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.