Métropole 11 mai 2022
Le directeur d’une grande entreprise a proposé à l’ensemble de ses salariés un stage de formation à l’utilisation d’un nouveau logiciel.
Ce stage a été suivi par 25 % des salariés.
1. Dans cette entreprise, 52 % des salariés sont des femmes, parmi lesquelles 40 % ont suivi le stage.
On interroge au hasard un salarié de l’entreprise et on considère les évènements :
• F : « le salarié interrogé est une femme »,
• S : « le salarié interrogé a suivi le stage ».
\overline{F} et \overline{S} désignent respectivement les évènements contraires des évènements F et S.
a. Donner la probabilité de l’évènement S.
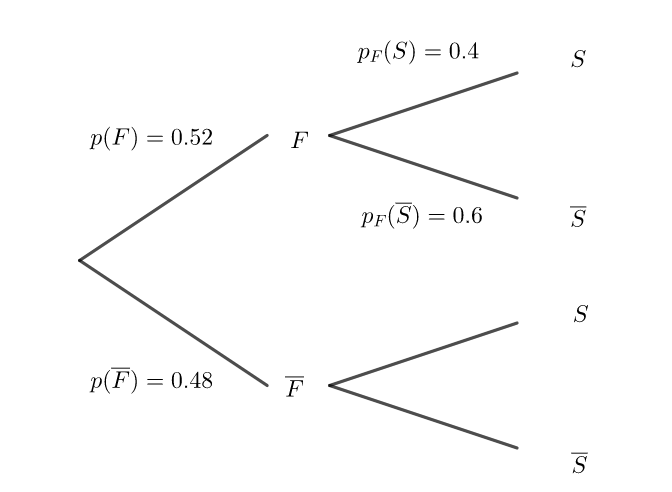
b. Recopier et compléter les pointillés de l’arbre pondéré ci-dessous sur les quatre branches indiquées.
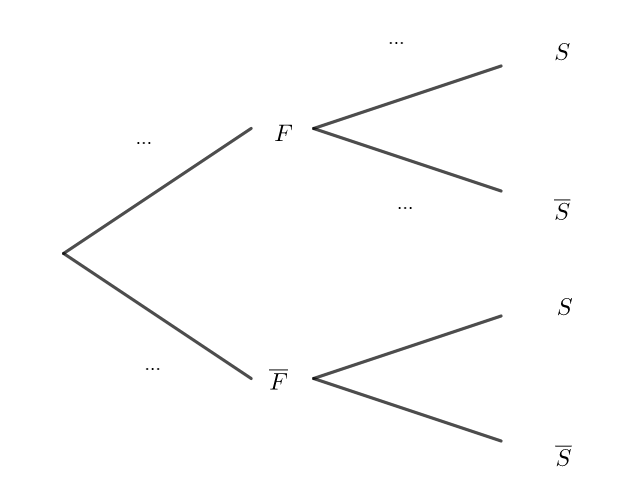
c. Démontrer que la probabilité que la personne interrogée soit une femme ayant suivi le stage est égale à 0.208.
d. On sait que la personne interrogée a suivi le stage. Quelle est la probabilité que ce soit une femme ?
e. Le directeur affirme que, parmi les hommes salariés de l’entreprise, moins de 10 % ont suivi le stage.
Justifier l’affirmation du directeur.
2. On note X la variable aléatoire qui à un échantillon de 20 salariés de cette entreprise choisis au hasard associe le nombre de salariés de cet échantillon ayant suivi le stage. On suppose que l’effectif des salariés de l’entreprise est suffisamment important pour assimiler ce choix à un tirage avec remise.
a. Déterminer, en justifiant, la loi de probabilité suivie par la variable aléatoire X
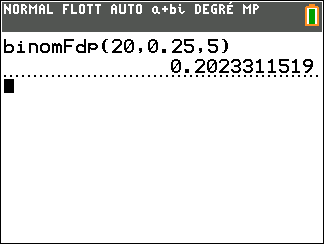
b. Déterminer, à 10^{-3} près, la probabilité que 5 salariés dans un échantillon de 20 aient suivi le stage.
c. Le programme ci-dessous, écrit en langage Python, utilise la fonction binomiale(i,n,p) créée pour l’occasion qui renvoie la valeur de la probabilité P(X=i) dans le cas où la variable aléatoire X suit une loi binomiale de paramètres n et p.

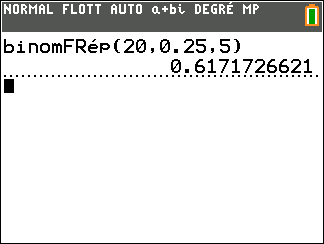
Déterminer, à 10^{-3} près, la valeur renvoyée par ce programme lorsque l’on saisit proba(5) dans la console Python.
Interpréter cette valeur dans le contexte de l’exercice.
d. Déterminer, à 10^{-3} près, la probabilité qu’au moins 6 salariés dans un échantillon de 20 aient suivi le stage.
3. Cette question est indépendante des questions 1 et 2.
Pour inciter les salariés à suivre le stage, l’entreprise avait décidé d’augmenter les salaires des salariés ayant suivi le stage de 5 %, contre 2 % d’augmentation pour les salariés n’ayant pas suivi le stage.
Quel est le pourcentage moyen d’augmentation des salaires de cette entreprise dans ces conditions ?