Les parties A et B peuvent être traitées de façon indépendante.
Au cours de la fabrication d’une paire de lunettes, la paire de verres doit subir deux traitements notés
T_1 et T_2.
Partie A
On prélève au hasard une paire de verres dans la production.
On désigne par A l’évènement : « la paire de verres présente un défaut pour le traitement T_1 ».
On désigne par B l’évènement : « la paire de verres présente un défaut pour le traitement T_2 ».
On note respectivement \overline{A} et \overline{B} les évènements contraires de A et B.
Une étude a montré que :
• la probabilité qu’une paire de verres présente un défaut pour le traitement T_1 notée P(A) est
égale à 0.1.
• la probabilité qu’une paire de verres présente un défaut pour le traitement T_2 notée P(B) est
égale à 0.2.
• la probabilité qu’une paire de verres ne présente aucun des deux défauts est 0.75.
1. Recopier et compléter le tableau suivant avec les probabilités correspondantes.
A | \overline{A} | Total | |
B | |||
\overline{B} | |||
Total |
2. a. Déterminer, en justifiant la réponse, la probabilité qu’une paire de verres, prélevée au hasard dans la production, présente un défaut pour au moins un des deux traitements T_1 ou T_2.
b. Donner la probabilité qu’une paire de verres, prélevée au hasard dans la production, présente deux défauts, un pour chaque traitement T_1 et T_2.
c. Les évènements A et B sont-ils indépendants ? Justifier la réponse.
3. Calculer la probabilité qu’une paire de verres, prélevée au hasard dans la production, présente un défaut pour un seul des deux traitements
4. Calculer la probabilité qu’une paire de verres, prélevée au hasard dans la production, présente
un défaut pour le traitement T_2, sachant que cette paire de verres présente un défaut pour le traitement T_1.
Partie B
On prélève, au hasard, un échantillon de 50 paires de verres dans la production. On suppose que la production est suffisamment importante pour assimiler ce prélèvement à un tirage avec remise.
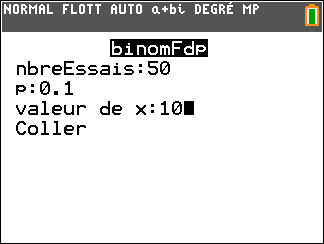
On note X la variable aléatoire qui, à chaque échantillon de ce type, associe le nombre de paires de verres qui présentent le défaut pour le traitement T_1.
1. Justifier que la variable aléatoire X suit une loi binomiale et préciser les paramètres de cette loi.
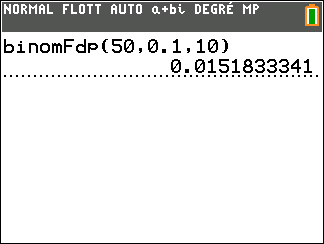
2. Donner l’expression permettant de calculer la probabilité d’avoir, dans un tel échantillon, exactement 10 paires de verres qui présentent le défaut pour le traitement T_1
Effectuer ce calcul et arrondir le résultat à 10^{-3}.
3. En moyenne, combien de paires de verres ayant le défaut pour le traitement T_1 peut-on trouver dans un échantillon
de 50 paires ?