logo

T. bac 2022 fonctions: exo n°2 ( Asie 17 mai 2022)

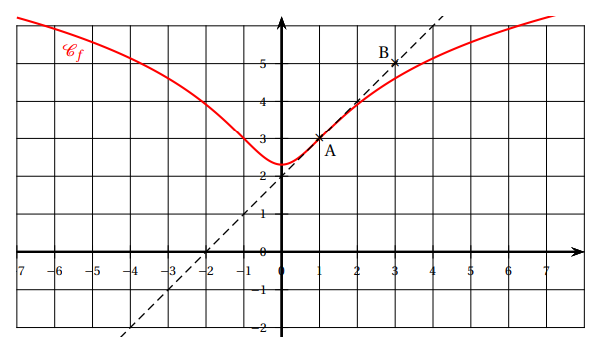
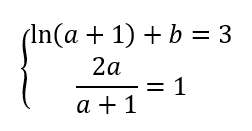Soit f une fonction définie et dérivable sur \mathbf{R}. On considère les points A(1;3) et B(3;5).
On donne ci-dessous C_f la courbe représentative de f dans un repère orthogonal du plan, ainsi que la tangente (AB) à la courbe C_f au point A.

Les trois parties de l’exercice peuvent être traitées de manière indépendante.
Partie A
1. Déterminer graphiquement les valeurs de f(1) et f'(1).

correction

2. La fonction f est définie par l’expression f(x)=ln(ax^2+1)+b, où a et b sont des nombres réels positifs.
a. Déterminer l’expression de f'(x).

correction

b. Déterminer les valeurs de a et b à l’aide des résultats précédents.

correction

Partie B
On admet que la fonction f est définie sur \mathbf{R} par
f(x)=ln(x^2+1)+3-ln(2)
1. Montrer que f est une fonction paire.

correction

2. Déterminer les limites de f en +\infty et en -\infty.

correction

3. Déterminer l’expression de f'(x)
Étudier le sens de variation de la fonction f sur \mathbf{R}.
Dresser le tableau des variations de f en y faisant figurer la valeur exacte du minimum ainsi que les limites de f en +\infty et en -\infty.

correction

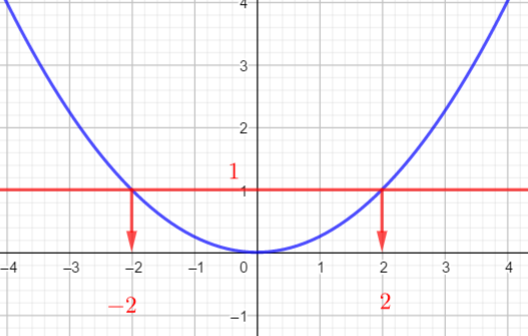
4. À l’aide du tableau des variations de f , donner les valeurs du réel f pour lesquelles l’équation f(x)=k admet deux solutions.

correction

5. Résoudre l’équation  f(x)=3+ln(2).

correction

Partie C
On rappelle que la fonction f est définie sur \mathbf{R} par
f(x)=ln(x^2+1)+3-ln(2).

1. Conjecturer, par lecture graphique, les abscisses des éventuels points d’inflexion de la
courbe C_f.

correction

2. Montrer que, pour tout nombre réel x, on a : f"(x)=\frac{2(1-x^2)}{(x^2+1)^2}.

correction

3. En déduire le plus grand intervalle sur lequel la fonction f est convexe.

correction

©2020 – Math’O karé SAS

On veut déterminer graphiquement f(1).

Je place 1 sur l’axe des abscisses.

Je trace la droite parallèle à l’axe des ordonnées passant par 1 jusqu’à la courbe

A partir du point de la courbe trouvé, je trace la droite parallèle à l’axe des abscisses  jusqu’à l’axe des ordonnées et je lis alors l’image de 1.

f(1)=3.

Pour valider ma réponse, je peux vérifier que le point qui a pour coordonnées :  1 et 3 est situé sur la courbe. C’est le point A.

On veut déterminer graphiquement f'(1).

Pour cela, il faut déterminer le coefficient directeur de la tangente à la courbe au point d’abscisse 1.

A partir du point A, j’avance  horizontalement d’une graduation et verticalement je monte d’une graduation pour retomber sur la tangente donc le coefficient directeur est positif et vaut 1.

f'(1)=1.

 

f(x)=ln(ax^2+1)+b, où a et b sont des nombres réels positifs.
On veut déterminer l’expression de f'(x).

C’est une somme, donc :

f'(x)=(ln(ax^2+1))’+(b)’

(b)’=0 car b est une constante.

f'(x)=(ln(ax^2+1))’

ln(ax^2+1) est de la forme ln(u(x)) avec u(x)=ax^2+1 donc u'(x)=2ax.

On remplace u(x) par ax^2+1 et u'(x) par 2ax dans \frac{u'(x)}{u(x)}.

f'(x)=\frac{2ax}{ax^2+1}.

On veut déterminer les valeurs de a et b à l’aide des résultats précédents.

On sait que f(1)=3 donc ln(a\times 1^2+1)+b=3.

On sait que f'(1)=1 donc \frac{2a\times 1}{a\times 1^2+1}=1.

On va donc résoudre le système de deux équations à deux inconnues suivant.

On résout la deuxième équation :

\frac{2a}{a+1}=1

2a=a+1

2a-a=1

a=1

On remplace a par 1 dans ln(a+1)+b=3.

ln(2)+b=3

b=3-ln(2).

Donc f(x)=ln(x^2+1)+3-ln(2).

 

On veut montrer que la fonction f définie sur \mathbf{R} est paire.

On vérifie que l’ensemble de définition est symétrique par rapport à 0, c’est le cas.

On calcule f(-x)

Pour cela on remplace tous les x par (-x) dans f(x)=ln(x^2+1)+3-ln(2)

f(-x)=ln((-x)^2+1)+3-ln(2)\\\hspace{1.05cm}=ln(x^2+1)+3-ln(2)\\\hspace{1.05cm}=f(x).

Donc la fonction f définie sur \mathbf{R} est paire.

 

On veut déterminer les limites de f en +\infty et en -\infty.

f(x)=ln(x^2+1)+3-ln(2).

On s’intéresse surtout à la fonction x\to ln(x^2+1)

La fonction x\to ln(x^2+1) est la composée de 2 fonctions, cliquer sur + La fonction est une composée, gof.

\lim f=lll+\infty-\infty+\infty
\lim g=l’+\infty-\infty+\infty-\infty-\infty
\lim f+g=l+l’+\infty-\infty+\infty-\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.

\lim f=ll\ne0\infty0
\lim g=l’\infty\infty\infty
\lim fg=l\times l’\infty\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

\lim f=ll\ne0l\infty\infty0
\lim g=l’\ne00\inftyl\infty0
\lim\frac{f}{g}=\frac{l}{l’}\infty0\inftyForme indéterminéeForme indéterminée

Remarque

quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

Si lim_{x\to a}\hspace{0.2cm}f(x)=b et lim_{X\to b}\hspace{0.2cm}g(X)=c alors lim_{x\to a}\hspace{0.2cm}g(f(x))=c

lim_{x\to -\infty}\hspace{0.2cm}x^2=+\infty\\lim_{x\to -\infty}\hspace{0.2cm}x^2+1=+\infty
lim_{X\to +\infty}\hspace{0.3cm}ln(X)=+\infty

Par fonction composée, lim_{x\to -\infty}\hspace{0.2cm}ln(x^2+1)=+\infty.

Par somme, lim_{x\to -\infty}\hspace{0.2cm}ln(x^2+1)+3-ln(2)=+\infty

Donc lim_{x\to -\infty}\hspace{0.2cm}f(x)=+\infty

lim_{x\to +\infty}\hspace{0.2cm}x^2=+\infty\\lim_{x\to +\infty}\hspace{0.2cm}x^2+1=+\infty
lim_{X\to +\infty}\hspace{0.3cm}ln(X)=+\infty

Par fonction composée, lim_{x\to +\infty}\hspace{0.2cm}ln(x^2+1)=+\infty.

Par somme, lim_{x\to +\infty}\hspace{0.2cm}ln(x^2+1)+3-ln(2)=+\infty

Donc lim_{x\to +\infty}\hspace{0.2cm}f(x)=+\infty

 

 

On a vu dans la partie A que f'(x)=\frac{2x}{x^2+1}.

Comme x^2+1>0, f'(x) est du signe de 2x.

Donc f'(x)<0 si x \in ]-\infty;0[ et f'(x)>0 si x \in ]0;+\infty[.

Comme f(0)=3-ln(2), on peut en déduire le tableau de variations suivant.

D’après le tableau de variations ci-dessous l’équation f(x)=k admet deux solutions si k>3-ln(2).

résoudre f(x)=3+ln(2)

c’est-à-dire : ln(x^2+1)+3-ln(2)=3+ln(2)

Etape n°1: On se ramène à une écriture de la forme  ln(a)=ln(b)

ln(x^2+1)+3-ln(2)=3+ln(2)\\ln(x^2+1)=3+ln(2)-3+ln(2)\\ln(x^2+1)=2ln(2)\\ln(x^2+1)=ln(2^2)\\ln(x^2+1)=ln(4)

Etape n°2 : On résout l’équation ln(x^2+1)=ln(4)

On peut appliquer la propriété suivante ln(x)=ln(y) \iff x=y.

ln(x^2+1)=ln(4) \iff x^2+1=4\\\hspace{2.9cm} \iff x^2=3\\\hspace{2.9cm} \iff x=-\sqrt{3} ou x=\sqrt{3}

Donc S=\{-\sqrt{3};\sqrt{3}\}

La fonction f définie sur \mathbf{R} est d’abord concave puis convexe puis concave.

En effet la courbe C_f est d’abord au-dessus de ses sécantes puis en-dessous et enfin au-dessus.

Il y a donc deux points d’inflexion.

f'(x)= \frac{2x}{x^2+1}

1.On veut calculer f"(x).

On répond à la question suivante : f'(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est le quotient de deux fonctions \frac{u}{ v} avec  u(x)=2x et v(x)=x^2+1.

On va utiliser la ligne n°5 du tableau n°1 ci-dessous.

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

2a.on veut calculer la dérivée  u'(x)

u(x)=2x

u'(x)=(2x)’

On utilise la ligne 2 du tableau 1 pour remplacer (2x)’ par 2(x)’

u'(x)=2(x)’

On utilise les lignes 1 (constante) et 2 (identité) du tableau 2 ci-dessous pour finir le calcul.

u'(x)=2\times1

u'(x)=2

2b.on veut calculer la dérivée  v'(x)

v(x)=x^2+1 est une somme, on utilise la 1ère ligne du tableau n°1 

v'(x)=(x^2+1)’

v'(x)=(x^2)’+(1)’

On utilise les lignes 1 (constante) et 3 (carré) du tableau 2 ci-dessous pour finir le calcul.

v'(x)=2x+0

v'(x)=2x

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}

3. On calcule la dérivée seconde f"(x) 

On remplace u par  2x,  v par x^2+1, u’ par  2 et v’ par 2x dans la formule \frac{u’\times v-u\times v’}{v^2} 

Voilà ce qu’il faut écrire sur votre copie :

f"(x)= (\frac{2x}{x^2+1})’\\\hspace{0.95cm}=\frac{(2x)’\times{(x^2+1)}-{(2x)}\times{(x^2+1)’}}{(x^2+1)^2}\\\hspace{0.95cm}=\frac{2\times{(x^2+1)}-{(2x)}\times{2x}}{(x^2+1)^2}\\\hspace{0.95cm}=\frac{2x^2+2-4x^2}{(x^2+1)^2} 

On réduit au numérateur

 f"(x)=\frac{-2x^2+2}{(x^2+1)^2}

On factorise au numérateur.

f"(x)=\frac{2(1-x^2)}{(x^2+1)^2} 

 

Pour déterminer le plus grand intervalle où  f est convexe, il faut résoudre l’inéquation  f"(x)> 0.

f"(x)=\frac{2(1-x^2)}{(x^2+1)^2}

Comme   (x^2+1)^2 et 2 sont strictement positifs, on va résoudre 1-x^2> 0.

Il n’est pas nécessaire de calculer le discrimant, on peut directement déterminer les racines de ce polynôme du second degré , c’est -1 et 1.

Comme a=-1, le polynôme est du signe de a à l’extérieur des racines et du signe de -a à l’intérieur.

Donc 1-x^2 est positif sur l’intervalle ]-1;1[ et donc le plus grand intervalle où  f est convexe est ]-1;1[.

 

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.