logo

T. bac 2022 fonctions exo n°3 ( Asie 18 mai 2022 )

Partie A

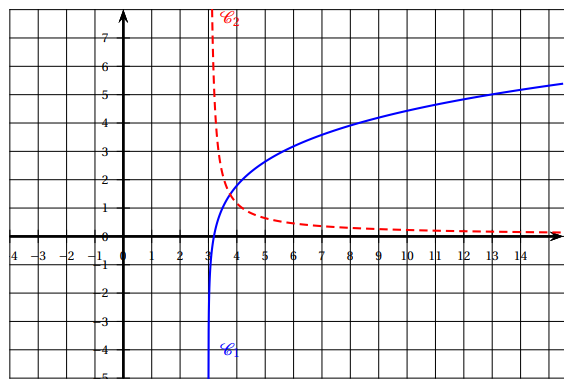
Dans le repère orthonormé ci-dessus, sont tracées les courbes représentatives d’une fonction f et de sa fonction dérivée, notée f’, toutes deux définies sur ]3;+\infty[ .
1. Associer à chaque courbe la fonction qu’elle représente. Justifier.

correction

2. Déterminer graphiquement la ou les solutions éventuelles de l’équation f(x)=3 .

correction

3. Indiquer, par lecture graphique, la convexité de la fonction f .

correction

Partie B
1. Justifier que la quantité ln(x^2-x-6) est bien définie pour les valeurs x de l’intervalle ]3;+\infty[ , que l’on nommera I dans la suite.

correction

2. On admet que la fonction f de la Partie A est définie par f(x)=ln(x^2-x-6) sur I.
Calculer les limites de la fonction f aux deux bornes de l’intervalle I.
En déduire une équation d’une asymptote à la courbe représentative de la fonction f sur I.

correction

3. a. Calculer f'(x) pour tout x appartenant à I

correction

3.b. Étudier le sens de variation de la fonction f sur I.
Dresser le tableau des variations de la fonction f en y faisant figurer les limites
aux bornes de I.

correction

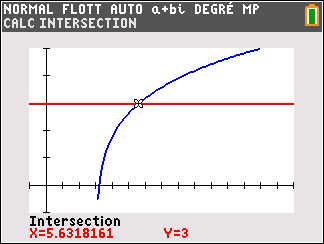
4. a. Justifier que l’équation f(x)=3 admet une unique solution \alpha sur l’intervalle ]5;6[.

correction

4.b. Déterminer, à l’aide de la calculatrice, un encadrement de \alpha à 10^{-2} près.

correction

5. a. Justifier que f"(x)=\frac{-2x^2+2x-13}{(x^2-x-6)^2}.

correction

5.b. Étudier la convexité de la fonction f sur I.

correction

©2020 – Math’O karé SAS

Possibilité n°1 : C_1 est la courbe de f et C_2 est la courbe de f’;

Comme C_2 est au-dessus de l’axe des abscisses, f'(x) est positif et donc f est croissante et C_1 monte.

Possibilité n°2 : C_1 est la courbe de f’ et C_2 est la courbe de f.

C_1 est en-dessous puis au-dessus de l’axe des abscisses, f'(x) est négative puis positive et donc f est décroissante puis croissante et C_1 descend puis monte.

Ce qui impossible compte-tenu de l’énoncé.

Résoudre graphiquement f(x)=3 revient à déterminer graphiquement le ou les antécédents de 3 s’il(s) existe(nt).

  • Je place 3 sur l’axe des ordonnées
  • Je trace la parallèle à l’axe des abscisses passant par 3 toute entière , d’un bord à l’autre du repère
  • Je repère les points d’intersection éventuels de la droite et de la courbe C_1
  • Je lis les abscisses de ces points d’intersections qui sont les antécédents de 3

L’antécédent de 3 est à peu près 5.5.

Graphiquement, l’équation f(x)=3 a pour ensemble solution S=\{5.5\}.

 

 

Graphiquement f semble concave sur un intervalle ]3;+\infty[ car pour tout x\in ]3;+\infty[, C_1 semble au-dessus de ses sécantes.

On veut justifier que la quantité ln(x^2-x-6) est bien définie pour les valeurs x de l’intervalle ]3;+\infty[ , que l’on nommera I dans la suite.

Il suffit simplement de montrer que la quantité x^2-x-6 est strictement positive sur ]3;+\infty[ .

On va étudier le signe de x^2-x-6 par le calcul.

J’identifie les coefficients l’équation a=1, b=-1 et c=-6.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1, (-1) ,(-6)  .

\Delta=(-1)²-4\times{1}\times{(-6)}\\\Delta=1+24\\\Delta=25

Comme \Delta>0 , l’équation admet deux solutions réelles notées

x_1=\frac{-b-\sqrt{\Delta}}{2a} et x_2=\frac{-b+\sqrt{\Delta}}{2a}.

ax²+bx+c est  du signe de a à l’extérieur des racines et du signe de (-a) à l’intérieur des racines.

Je calcule x_1=\frac{-b-\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par 1, (-1), 25.

x_1=\frac{-(-1)-\sqrt{25}}{2\times{1}}\\x_1=\frac{1-5}{2}\\x_1=-\frac{4}{2}\\x_1=-2.

Je calcule x_2=\frac{-b+\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par 1,(-1), 25.

x_2=\frac{-(-1)+\sqrt{25}}{2\times{1}}\\x_2=\frac{1+5}{2}\\x_2=\frac{6}{2}.

x_2=3.

Je dresse le tableau de signes du polynôme:

Comme a=1 le signe de a est positif.

D’après le tableau de signes, x^2-x-6 est strictement positif sur ]3;+\infty[.

Ainsi la quantité ln(x^2-x-6) est bien définie pour les valeurs x de l’intervalle ]3;+\infty[ .

 

On veut déterminer les limites de f en 3 et en +\infty.

f(x)=ln(x^2-x-6).

La fonction x\to ln(x^2-x+6) est la composée de 2 fonctions, cliquer sur + La fonction est une composée, gof.

\lim f=lll+\infty-\infty+\infty
\lim g=l’+\infty-\infty+\infty-\infty-\infty
\lim f+g=l+l’+\infty-\infty+\infty-\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en factorisant et on applique un autre théorème par exemple celui sur le produit.

\lim f=ll\ne0\infty0
\lim g=l’\infty\infty\infty
\lim fg=l\times l’\infty\inftyForme indéterminée

Remarque quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en développant et on applique un autre théorème par exemple celui sur la somme.

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

\lim f=ll\ne0l\infty\infty0
\lim g=l’\ne00\inftyl\infty0
\lim\frac{f}{g}=\frac{l}{l’}\infty0\inftyForme indéterminéeForme indéterminée

Remarque

quand on dit « forme indéterminée » cela signifie que le théorème ne permet pas de conclure. On modifie l’écriture par exemple en simplifiant le quotient et on applique à nouveau le théorème .

Dans le tableau, on a noté \infty sans préciser le signe, il suffira d’appliquer le règle des signes pour conclure.

Si lim_{x\to a}\hspace{0.2cm}f(x)=b et lim_{X\to b}\hspace{0.2cm}g(X)=c alors lim_{x\to a}\hspace{0.2cm}g(f(x))=c

Calcul de lim_{x\to 3}\hspace{0.2cm}f(x).

lim_{x\to 3}\hspace{0.2cm}x^2-x-6=9-3-6=0
lim_{X\to 0}\hspace{0.3cm}ln(X)=-\infty

Par fonction composée, lim_{x\to 3}\hspace{0.2cm}ln(x^2-x-6)=-\infty.

Donc lim_{x\to 3}\hspace{0.2cm}f(x)=-\infty et donc la droite verticale d’équation x=3 est asymptote à courbe représentative de la fonction f sur I soit C_1.

Calcul de lim_{x\to +\infty}\hspace{0.2cm}f(x).

On veut calculer lim_{x\to +\infty}\hspace{0.2cm}x^2-x-6 mais on obtient une forme indéterminée. On met x^2 en facteur et on applique le théorème sur le produit.

lim_{x\to +\infty}\hspace{0.2cm}x^2-x-6=lim_{x\to +\infty}\hspace{0.2cm}x^2(1-\frac{1}{x}-\frac{6}{x^2})\\\hspace{3.25cm}=+\infty

car

lim_{x\to +\infty}\hspace{0.2cm}x^2=+\infty et lim_{x\to +\infty}\hspace{0.2cm}(1-\frac{1}{x}-\frac{6}{x^2})=1.

lim_{X\to +\infty}\hspace{0.3cm}ln(X)=+\infty

Par fonction composée, lim_{x\to +\infty}\hspace{0.2cm}ln(x^2-x-6)=+\infty

Donc lim_{x\to +\infty}\hspace{0.2cm}f(x)=+\infty

 On veut calculer la dérivée de f(x)=ln(x^2-x-6).

ln(x^2-x-6) est de la forme ln(u(x)) avec u(x)=x^2-x-6 donc u'(x)=2x-1.

On remplace u(x) par x^2-x-6 et u'(x) par 2x-1 dans \frac{u'(x)}{u(x)}.

f'(x)=\frac{2x-1}{x^2-x-6}.

On veut étudier le sens de variation de la fonction f sur I.
 f'(x)=\frac{2x-1}{x^2-x-6}.

On a montré que x^2-x-6>0 sur I.

De plus 2x-1>0 sur I.

Donc f'(x) est positive sur I.

Donc f est croissante sur I.

De plus lim_{x\to 3}\hspace{0.2cm}f(x)=-\infty et lim_{x\to +\infty}\hspace{0.2cm}f(x)=+\infty

On dresse ensuite le tableau des variations de la fonction f en y faisant figurer les limites aux bornes de I

On va justifier que l’équation f(x)=3 admet une unique solution  que l’on notera \alpha dans ]5;6[. 

On visualise le phénomène sur le tableau de variations.

A l’aide de la calculatrice, on détermine :

f(5)=2.64 et f(6)=3.18.

Sur l’intervalle ]5;6[ la fonction f est  continue et  strictement croissante.

Comme  3\in]2.64;3.18] alors l’équation f(x)=3 admet une unique solution notée \alpha sur l’intervalle ]5;6[.

Au clavier

A l’écran

Taper sur la touche f(x) en haut à gauche du clavier de la calculatrice.

En général le mode fonction est activé par défaut.

Si ce n’est pas le cas, taper sur la touche mode et sélectionner FONCTION sur la 5ème ligne. Puis quitter avec 2nde mode

On programme la fonction en complétant la ligne Y1= . Pour saisir x taper au clavier sur la touche X,T,O,n.

Puis taper Y2=3

Taper sur la touche  graphe

Taper sur la touche 2nde et la touche trace puis sélectionner 5:intersection dans le menu. Appuyer sur entrer.

Appuyer sur entrer deux  fois.Puis taper par exemple 5 au clavier pour saisir la valeur initiale ( la valeur choisie doit être inférieure à l’abscisse du point d’intersection des deux courbes).

On fait entrer et on peut lire en bas de l’écran la valeur de \alpha.

Il ne reste plus qu’à donner un encadrement de \alpha à 10^{-2} près.

5.63<\alpha <5.64.

 

On veut justifier que f"(x)=\frac{-2x^2+2x-13}{(x^2-x-6)^2}

f'(x)= \frac{2x-1}{x^2-x-6}

1.On veut calculer f"(x).

On répond à la question suivante : f'(x) est-elle une somme, le produit d’un réel par une fonction, le produit de deux fonctions, l’inverse d’une fonction ou le quotient de deux fonctions ?

C’est le quotient de deux fonctions \frac{u}{ v} avec  u(x)=2x-1 et v(x)=x^2-x-6.

On va utiliser la ligne n°5 du tableau n°1 ci-dessous.

f(x) est 

f'(x) se calcule ainsi :

une somme u+v

u’+v’

le produit d’une constante k par une fonction u c’est-à-dire ku

k\times u’

un produit de deux fonctions u\times v

u’\times v+u\times v’

l’inverse d’une fonction \frac{1}{u}

-\frac{u’}{u^2}

un quotient \frac{u}{v}

 \frac{u’\times v-u\times v’}{v^2}

2a.on veut calculer la dérivée  u'(x)

u(x)=2x-1

u'(x)=(2x)’-(1)’

u'(x)=2(x)’-0

u'(x)=2\times1

u'(x)=2

2b.on veut calculer la dérivée  v'(x)

v(x)=x^2-x-6 est une somme, on utilise la 1ère ligne du tableau n°1 

v'(x)=(x^2-x-6)’

v'(x)=(x^2)’-(x)’-(6)’

v'(x)=2x-1-0

v'(x)=2x-1

Fonction

f(x)

Dérivable sur…

f'(x)

constante

f(x)=k\mathbf{R}f'(x)=0

identité

f(x)=x\mathbf{R}f'(x)=1

carré

f(x)=x^2\mathbf{R}f'(x)=2x

cube

f(x)=x^3\mathbf{R}f'(x)=3x^2

inverse 

f(x)=\frac{1}{x}\left]-\infty;0\right[\cup\left]0;+\infty\right[f'(x)=-\frac{1}{x^2}

racine carrée

f(x)=\sqrt{x}]0;+\infty[f'(x)=\frac{1}{2\sqrt{x}}

3. On calcule la dérivée seconde f"(x) 

On remplace u par  2x-1,  v par x^2-x-6, u’ par  2 et v’ par 2x-1 dans la formule \frac{u’\times v-u\times v’}{v^2} 

Voilà ce qu’il faut écrire sur votre copie :

f"(x)= (\frac{2x-1}{x^2-x-6})’\\\hspace{0.95cm}=\frac{(2x-1)’\times{(x^2-x-6)}-{(2x-1)}\times{(x^2-x-6)’}}{(x^2-x-6)^2}\\\hspace{0.95cm}=\frac{2\times{(x^2-x-6)}-{(2x-1)}\times{(2x-1)}}{(x^2-x-6)^2}\\\hspace{0.95cm}=\frac{2x^2-2x-12-(4x^2-4x+1)}{(x^2-x-6)^2}\\\hspace{0.95cm}=\frac{2x^2-2x-12-4x^2+4x-1}{(x^2-x-6)^2} 

On réduit au numérateur

 f"(x)=\frac{-2x^2+2x-13}{(x^2-x-6)^2}

 

Pour étudier la convexité de f, il faut étudier le signe de f"(x).

f"(x)=\frac{-2x^2+2x-13}{(x^2-x-6)^2}

Comme   (x^2-x-6)^2 est positif, on va étudier le signe de -2x^2+2x-13.

On calcule le discrimant

a=-2, b=2 et c=-13.

\Delta=2^2-4\times (-2)\times (-13)=-100

Comme \Delta<0, le polynôme -2x^2+2x-13 est toujours du signe de a donc négatif.

Donc le quotient \frac{-2x^2+2x-13}{(x^2-x-6)^2} est négatif sur I, donc f"(x) est négatif sur I donc f est concave sur I.  

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.