Lors d’une kermesse, un organisateur de jeux dispose, d’une part, d’une roue comportant quatre cases blanches et huit cases rouges et, d’autre part, d’un sac contenant cinq jetons portant les numéros 1, 2, 3, 4 et 5.
Le jeu consiste à faire tourner la roue, chaque case ayant la même probabilité d’être obtenue, puis à extraire un ou deux jetons du sac selon la règle suivante :
• si la case obtenue par la roue est blanche, alors le joueur extrait un jeton du sac;
• si la case obtenue par la roue est rouge, alors le joueur extrait successivement et sans remise deux jetons du sac.
Le joueur gagne si le ou les jetons tirés portent tous un numéro impair.
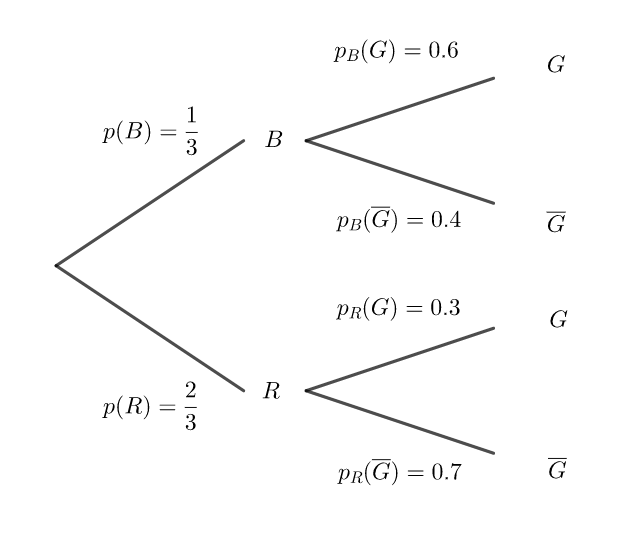
1. Un joueur fait une partie et on note B l’évènement « la case obtenue est blanche », R l’évènement « la case obtenue est rouge » et G l’évènement « le joueur gagne la partie ».
a. Donner la valeur de la probabilité conditionnelle p_B(G).
b. On admettra que la probabilité de tirer successivement et sans remise deux jetons impairs est égale à 0,3.
Recopier et compléter l’arbre de probabilité suivant :
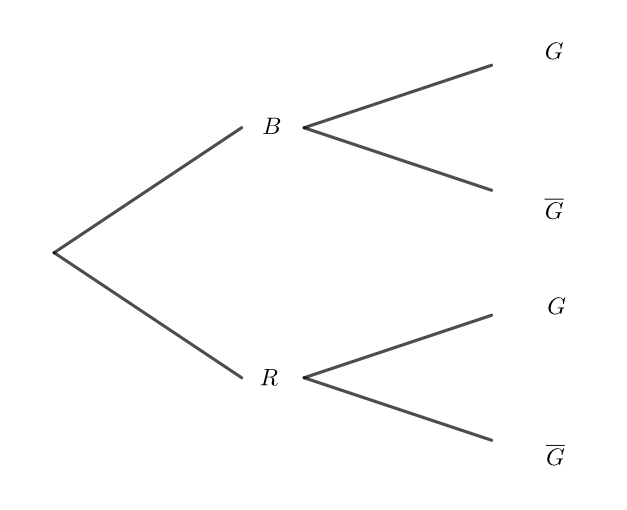
2. a. Montrer que p(G)=0.4
2. b. Un joueur gagne la partie.
Quelle est la probabilité qu’il ait obtenu une case blanche en lançant la roue ?
3. Les évènements B et G sont-ils indépendants ? Justifier.
4. Un même joueur fait dix parties. Les jetons tirés sont remis dans le sac après chaque partie.
On note X la variable aléatoire égale au nombre de parties gagnées.
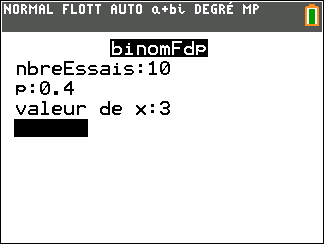
a. Expliquer pourquoi X suit une loi binomiale et préciser ses paramètres.
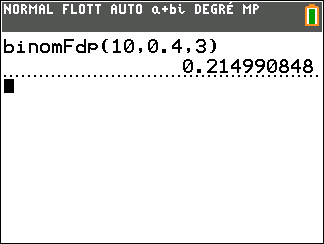
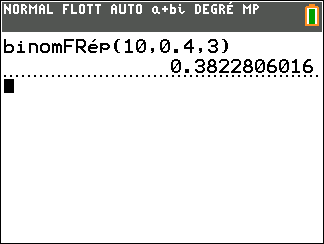
b. Calculer la probabilité, arrondie à 10^{-3} près, que le joueur gagne exactement trois parties sur les dix parties jouées.
c. Calculer p(X\geq 4) arrondie à 10^{-3} près.
Donner une interprétation du résultat obtenu.
5. Un joueur fait n parties et on note p_n la probabilité de l’évènement « le joueur gagne au moins une partie ».
a. Montrer que p_n=1-0.6^n.
b. Déterminer la plus petite valeur de l’entier n pour laquelle la probabilité de gagner au moins une partie est supérieure ou égale à 0.99.