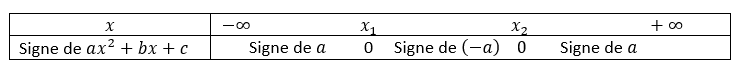T. bac 2022 fonctions exo n°5 ( Nouvelle calédonie 26 Octobre 2022 )

ANALYSE, Exercices bac 2022 : les fonctions, Niveau terminale spécialité

Voici la courbe de la fonction $f$ définie sur l’intervalle $]0 ; +∞[$ par $f (x) = x^2 −6x +4ln(x)$ dans une fenêtre active Géogébra.

On considère la fonction $f$ définie sur l’intervalle $]0 ; +∞[$ par $f (x) = x^2 −6x +4ln(x)$
On admet que la fonction $f$ est deux fois dérivable sur l’intervalle $]0 ; +∞[$ .
On note $f’$ sa dérivée et $f"$ sa dérivée seconde.
On note $C_f$ la courbe représentative de la fonction $f$ dans un repère orthogonal.
1. a. Déterminer $lim_{x\to 0}\hspace{0.2cm}f(x)$ .

On observe la courbe pour se faire une idée du résultat (attention la lecture graphique se limite à la fenêtre d’affichage et on peut parfois avoir des surprises)

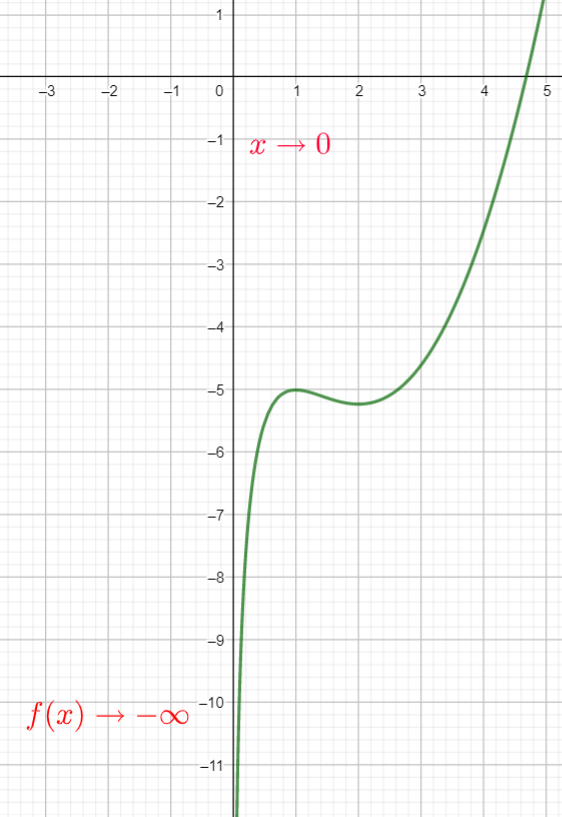
Interpréter graphiquement ce résultat.

1. b. Déterminer $lim_{x\to +\infty}\hspace{0.2cm}f(x)$ .

On observe la courbe pour se faire une idée du résultat (attention la lecture graphique se limite à la fenêtre d’affichage et on peut parfois avoir des surprises)

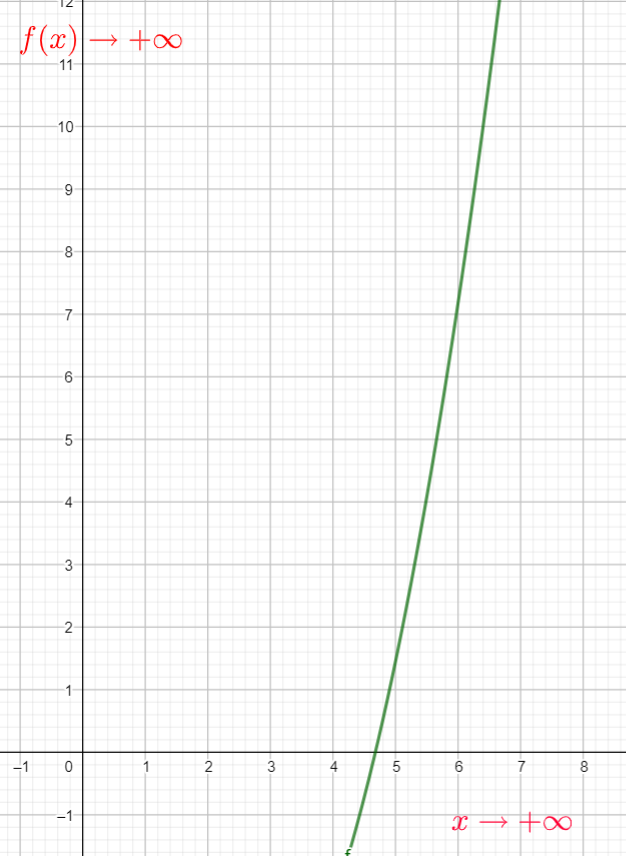
2. a. Déterminer $f'(x)$ pour $x$ appartenant à l’intervalle $]0 ; +∞[$ .

Taper f'(x)= dans la colonne du milieu : celle du calcul formel, faire entrer et la dérivée apparaît.

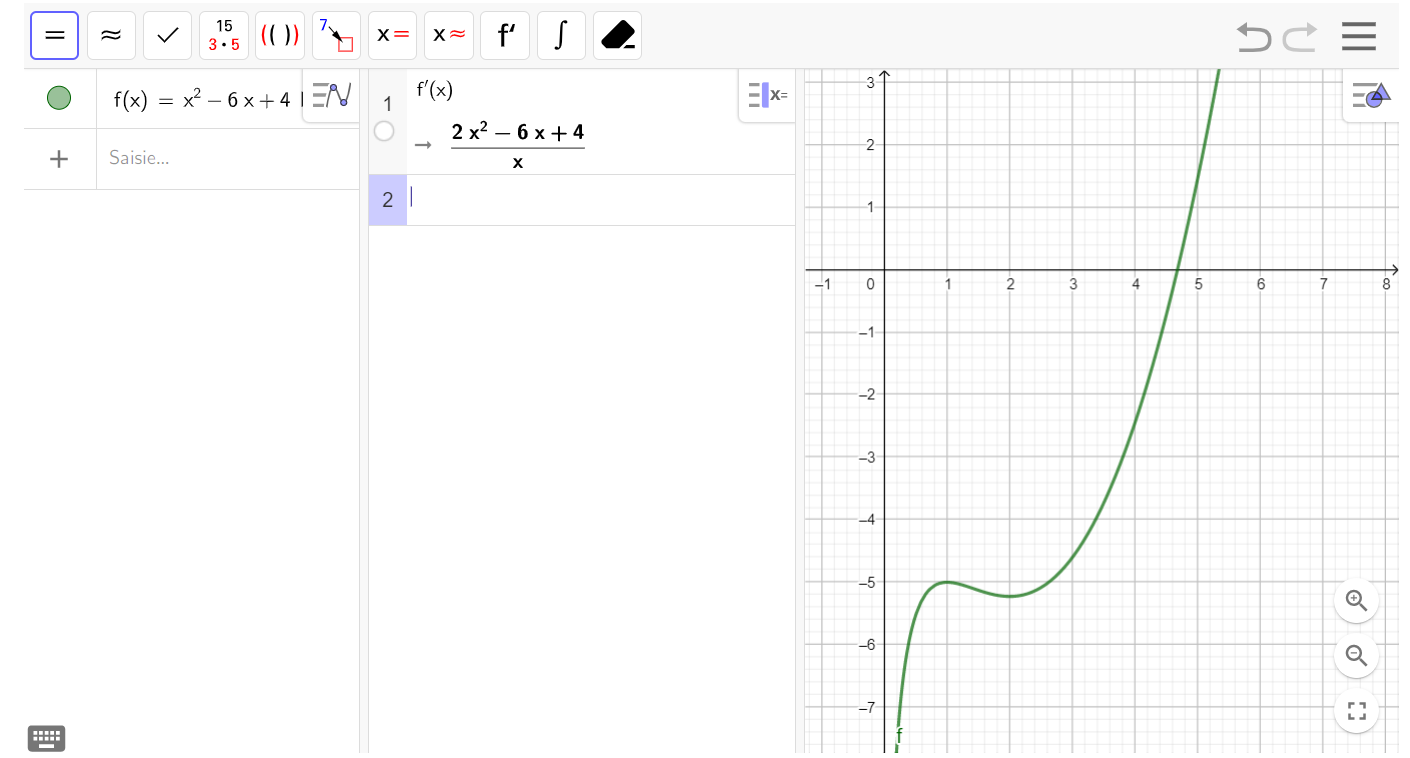
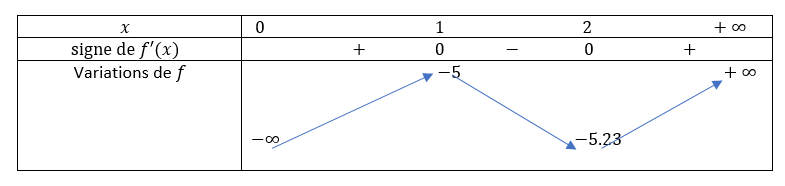
2. b. Étudier le signe de $f'(x)$ sur l’intervalle $]0 ; +∞[$ .
En déduire le tableau de variations de $f$ sur l’intervalle $]0 ; +∞[$ .

Pour conjecturer les variations, on peut cliquer gauche sur les trois points verticaux situés à droite de $f (x) = x^2 −6x +4ln(x)$ dans la première colonne et sélectionner Points spéciaux dans le menu déroulant. On peut lire les coordonnées des extremums. Graphiquement, la courbe monte jusqu’à x=1, descend jusqu’à x=2 puis monte.

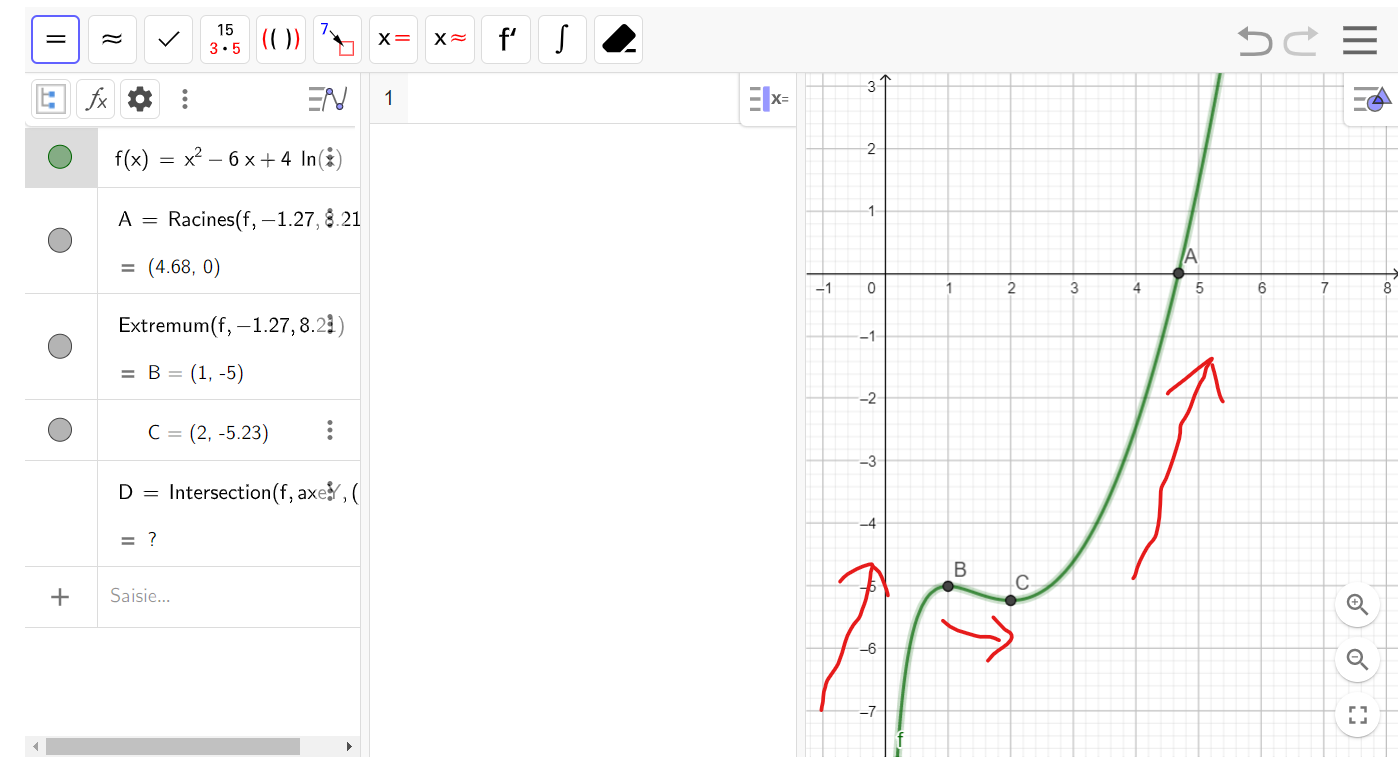
3. Montrer que l’équation $f(x)=0$ admet une unique solution dans l’intervalle $[4;5]$ .

Pour visualiser le phénomène, on peut cliquer gauche sur les trois points verticaux situés à droite de $f (x) = x^2 −6x +4ln(x)$ dans la première colonne et sélectionner Points spéciaux dans le menu déroulant. Le point A est le point d’intersection de la courbe et de l’axe des ordonnées.

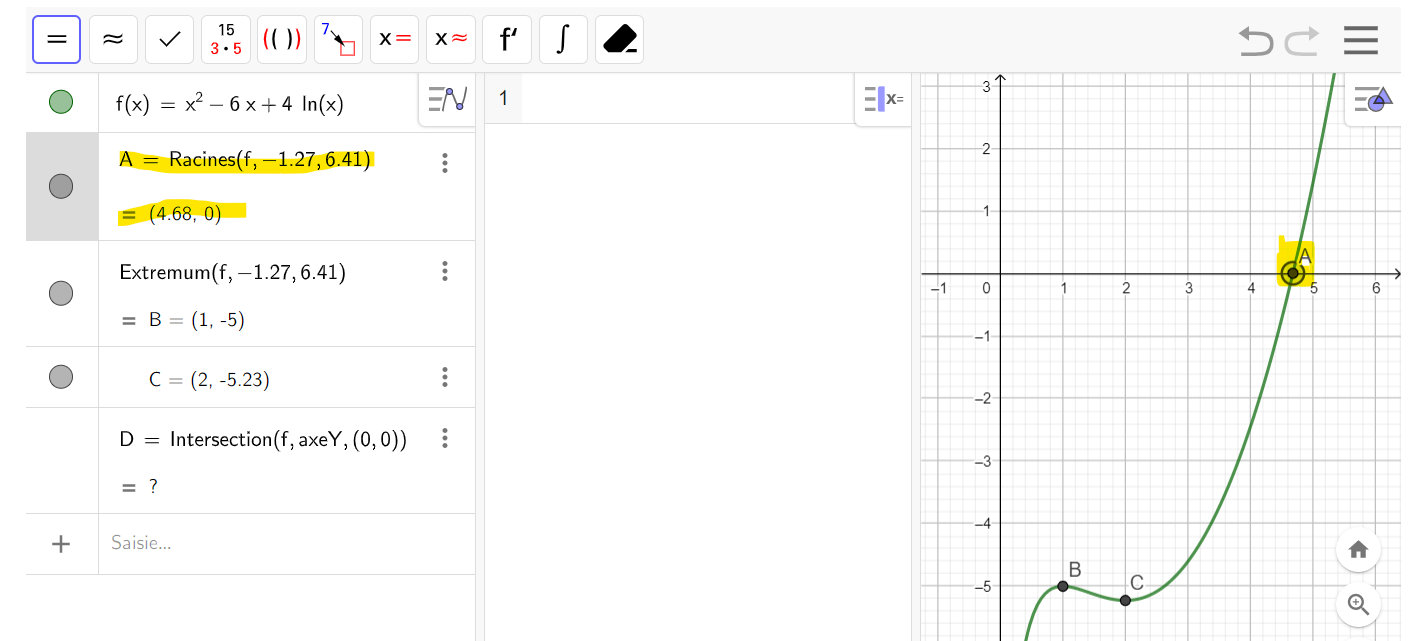
4. On admet que, pour tout $x$ appartenant à l’intervalle $]0 ; +∞[$ , on a :
$f"(x)=\frac{2x^2-4}{x^2}$ .
a. Étudier la convexité de la fonction $f$ sur l’intervalle $]0 ; +∞[$ .
On précisera les valeurs exactes des coordonnées des éventuels points d’inflexion de $C_f$ .

b. On note $A$ le point de coordonnées $(\sqrt{2},f(\sqrt{2}))$ .
Soit $t$ un réel strictement positif tel que $t\ne \sqrt{2}$
Soit $M$ le point de coordonnées $(t,f(t))$
En utilisant la question 4. a, indiquer, selon la valeur de $t$ , les positions relatives du segment $[AM]$ et de la courbe $C_f$ .