logo

T. bac2022 suites exo n°3 ( nouvelle calédonie 27 Octobre 2022 )

Cet exercice est un questionnaire à choix multiples.
Pour chacune des questions suivantes, une seule des quatre réponses proposées est exacte.
Une réponse fausse, une réponse multiple ou l’absence de réponse à une question ne rapporte ni n’enlève de point.
Pour répondre, indiquer sur la copie le numéro de la question et la lettre de la réponse choisie.
Aucune justification n’est demandée.
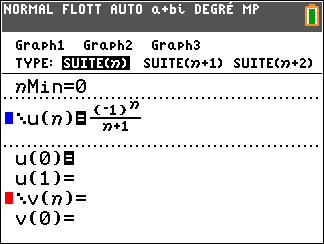
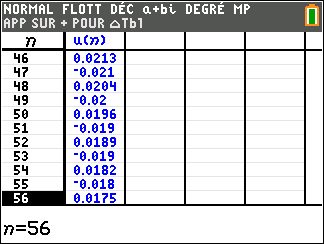
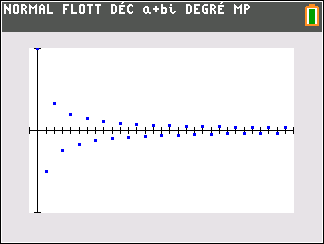
1. On considère la suite (u_n) définie pour tout entier naturel n par
u_n=\frac{(-1)^n}{n+1}
On peut affirmer que :

a.La suite (u_n) diverge vers +\infty.

b.La suite (u_n) diverge vers -\infty.

c.La suite (u_n) n’a pas de limite.

d.La suite (u_n) converge.

correction n°1 : avec la TI 83 Premium CE
correction n°2

Dans les questions 2 et 3, on considère deux suites (v_n) et (w_n) vérifiant la relation : w_n=e^{-2v_n}+2
2. Soit a un nombre réel strictement positif. On a v_0=ln(a).

a. w_0=\frac{1}{a^2}+2

b. w_0=\frac{1}{a^2+2}

c. w_0=-2a+2

d. w_0=\frac{1}{-2a}+2

correction

3. On sait que la suite (v_n) est croissante. On peut affirmer que la suite (w_n) est :

a. décroissante et majorée par 3.

b. décroissante et minorée par 2.

c. croissante et majorée par 3.

d. croissante et minorée par 2.

correction

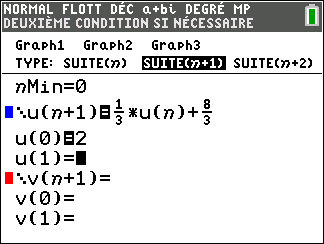
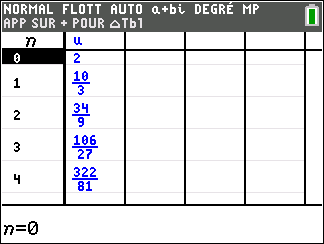
4. On considère la suite (a_n) ainsi définie :
a_0=2 et, pour tout entier naturel n, a_{n+1}=\frac{1}{3}a_n+\frac{8}{3}.
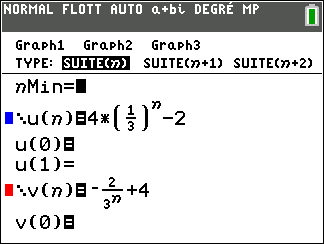
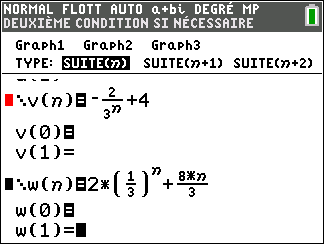
Pour tout entier naturel n, on a :

a. a_n=4\times (\frac{1}{3})^n-2

b. a_n=-\frac{2}{3^n}+4

c. a_n=4-(\frac{1}{3})^n

b. a_n=2\times (\frac{1}{3})^n+\frac{8n}{3}

correction

5. On considère une suite (b_n) telle que, pour tout entier naturel n, on a :
b_{n+1}=b_n+ln(\frac{2}{(b_n)^2+3})
On peut affirmer que :

a. la suite (b_n) est croissante.

b. la suite (b_n) est décroissante.

c. la suite (b_n) n’est pas monotone.

d. le sens de variation de la suite (b_n) dépend de b_0.

correction

©2020 – Math’O karé SAS

Voici comment programmer sa TI 83 Premium CE pour faire apparaître le tableur ou le graphe.

On voit que les termes u_n se rapprochent de 0, la suite (u_n) converge vers 0.

La bonne réponse est la réponse d

Au clavier

A l’écran

Taper sur la touche mode et sélectionner SUITE sur la 5ème ligne. Puis quitter avec 2nde mode

Taper ensuite sur la touche f(x) en haut à gauche. Comme la suite  est définie par formule explicite, à l’aide des flèches, dans TYPE sélectionner SUITE(n).

On programme la suite

Pour cela sur la ligne nMin saisir  le plus petit rang, c’est souvent 0 mais il arrive que ce soit 1 ou autre chose. 

Puis compléter la ligne u(n+1)=. Pour saisir n taper au clavier sur la touche X,T,O,n et pour saisir u taper sur la touche 2nde puis sur la touche 7.

Il n’est pas nécessaire de compléter la ligne u(0)=

Pour afficher les termes de la suite, s’assurer que le tableur est bien paramétré, faire 2nde puis fenêtre on doit avoir 0, 1, AUTO et AUTO.

Taper sur la touche 2nde et sur la touche graphe, le tableur apparaît.

On descend dans le tableau pour voir vers quelle valeur semble se rapprocher les termes de la suite.

Compte-tenu du tableur obtenu précédemment, on modifie l’affichage du graphique en tapant sur la touche fenêtre et en modifiant les valeurs déjà présentes.

Voici par exemple, un paramétrage possible.

Taper sur la touche graphe, le graphique apparaît.

On a u_n=\frac{(-1)^n}{n+1}.

On va utiliser le théorème des gendarmes.

-1\leq (-1)^n \leq 1\\ \frac{-1}{n+1} \leq \frac{(-1)^n}{n+1} \leq \frac{1}{n+1}

Comme lim_{n\to+\infty}\hspace{0.2cm}\frac{-1}{n+1}=0 et lim_{n\to+\infty}\hspace{0.2cm}\frac{1}{n+1}=0, d’après le théorème des gendarmes :

lim_{n\to+\infty}\hspace{0.2cm}\frac{(-1)^n}{n+1}=0

Donc 

lim_{n\to+\infty}\hspace{0.2cm}u_n=0 et ainsi la suite (u_n) converge.

La bonne réponse est la réponse d.

 

On a v_0=ln(a).

Calculons w_0 en remplaçant v_0 par ln(a) dans w_0=e^{-2v_0}+2.

w_0=e^{-2v_0}+2\\\hspace{0.5cm}=e^{-2ln(a)}+2\\\hspace{0.5cm}=\frac{1}{e^{2ln(a)}}+2\\\hspace{0.5cm}=\frac{1}{e^{ln(a^2)}}+2\\\hspace{0.5cm}=\frac{1}{a^2}+2

La bonne réponse est la réponse a.

On veut étudier les varaitions de la suite (w_n).

On peut décomposer la séquence de calcul de w_n. Cette décomposition nous donnera la procédure pour déterminer les variations de (w_n).

\hspace{0.1cm}\times(-2)\hspace{0.5cm}exp()\hspace{0.55cm}+2 \\v_n\to -2v_n\to  e^{-2v_n}\to e^{-2v_n}+2

On sait que la suite (v_n) est croissante :

v_n \leq v_{n+1}

On multiplie par (-2) qui est négatif, l’inégalité change de sens.

-2v_n \geq -2v_{n+1}

La fonction exponentielle est croissante : les nombres et les images varient dans le même sens.

e^{-2v_n} \geq e^{-2v_{n+1}}

On ajoute 2 , l’inégalité ne change pas de sens.

e^{-2v_n}+2 \geq e^{-2v_{n+1}}+2

Donc 

w_n \geq w_{n+1}

Donc la suite (w_n) est décroissante.

On sait que  e^{-2v_n}>0 donc e^{-2v_n}+2>0+2 donc w_n>2 donc (w_n) est minorée par 2 .

Donc la bonne réponse est la réponse b

On commence par programmer la suite  (a_n) par récurrence en utilisant  a_{n+1}=\frac{1}{3}a_n+\frac{8}{3} et a_{0}=2.

Au clavier

A l’écran

Taper sur la touche mode et sélectionner SUITE sur la 5ème ligne. Puis quitter avec 2nde mode

Taper ensuite sur la touche f(x) en haut à gauche. Comme la suite  est définie par récurrence, à l’aide des flèches, dans TYPE sélectionner SUITE(n+1).

On programme la suite

Pour cela sur la ligne nMin saisir  le plus petit rang, c’est souvent 0 mais il arrive que ce soit 1 ou autre chose. 

Puis compléter la ligne u(n+1)=. Pour saisir n taper au clavier sur la touche X,T,O,n et pour saisir u taper sur la touche 2nde puis sur la touche 7.

Compléter la ligne u(0)=2.

Pour afficher les termes de la suite, s’assurer que le tableur est bien paramétré, faire 2nde puis fenêtre on doit avoir 0, 1, AUTO et AUTO.

Taper sur la touche 2nde et sur la touche graphe, le tableur apparaît.

 

Ensuite on calcule a_0 mentalement en remplaçant n par 0 dans les quatre réponses. On obtient 2 pour trois réponses et 3 pour la réponse c.

On programme ensuite les trois suites des réponses a, b et d et on regarde quelle suite donne les mêmes valeurs que le tableau précédent.

Au clavier

A l’écran

Taper sur la touche mode et sélectionner SUITE sur la 5ème ligne. Puis quitter avec 2nde mode

Taper ensuite sur la touche f(x) en haut à gauche. Comme la suite  est définie par formule explicite, à l’aide des flèches, dans TYPE sélectionner SUITE(n).

On programme les trois suites.

Pour cela sur la ligne nMin saisir  le plus petit rang, c’est souvent 0 mais il arrive que ce soit 1 ou autre chose. 

Puis compléter la ligne u(n+1)=. Pour saisir n taper au clavier sur la touche X,T,O,n et pour saisir u taper sur la touche 2nde puis sur la touche 7.

Continuer pour les autres suites.

Pour afficher les termes de la suite, s’assurer que le tableur est bien paramétré, faire 2nde puis fenêtre on doit avoir 0, 1, AUTO et AUTO.

Taper sur la touche 2nde et sur la touche graphe, le tableur apparaît.

On descend dans le tableau pour voir vers quelle valeur semble se rapprocher les termes de la suite.

On retrouve les mêmes valeurs dans la colonne de v_n=-\frac{2}{3^n}+4.

Donc la bonne réponse est la réponse b

On considère une suite (b_n) telle que, pour tout entier naturel n, on a :
b_{n+1}=b_n+ln(\frac{2}{(b_n)^2+3}).

On s’intéresse aux variations de la suite (b_n).

En enlevant b_n de chaque côté de l’égalité b_{n+1}=b_n+ln(\frac{2}{(b_n)^2+3}), on ne devrait pas avoir trop de mal à déterminer le signe de b_{n+1}-b_n.

b_{n+1}-b_n=ln(\frac{2}{(b_n)^2+3})

Pour déterminer le signe de ln(\frac{2}{(b_n)^2+3}), il faut comparer \frac{2}{(b_n)^2+3} à 1.

(b_n)^2>0\\(b_n)^2+3>3

La fonction inverse est décroissante, les nombres et leurs images varient en sens contraire.

\frac{1}{(b_n)^2+3}<\frac{1}{3}\\\frac{2}{(b_n)^2+3}<\frac{2}{3}, or \frac{2}{3}<1 donc :

\frac{2}{(b_n)^2+3}<1

La fonction ln est croissante, les nombres et leurs images varient dans le même sens.

ln(\frac{2}{(b_n)^2+3})<ln(1)\\ln(\frac{2}{(b_n)^2+3})<0

Donc ln(\frac{2}{(b_n)^2+3}) est négatif.

Donc b_{n+1}-b_n est négatif.

Donc la suite (b_n) est décroissante.

Donc la bonne réponse est la réponse b.

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.