logo

T. bac2022 suites exo n°4 ( Amérique du Nord 18 mai 2022 )

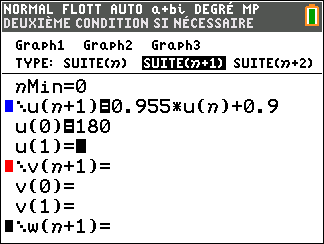
Dans cet exercice, on considère la suite (T_n) définie par :
T_0=180 et, pour tout entier naturel n, T_{n+1}=0.955T_n+0.9
1. a. Démontrer par récurrence que, pour tout entier naturel n, T_n\geq 20.

correction

b. Vérifier que pour tout entier naturel n, T_{n+1}-T_n=-0.045(T_n-20). En déduire le sens de variation de la suite (T_n).

correction

c. Conclure de ce qui précède que la suite (T_n) est convergente. Justifier.

correction

2. Pour tout entier naturel n, on pose : u_n=T_n-20.
a. Montrer que la suite (u_n) est une suite géométrique dont on précisera la raison.

correction

b. En déduire que pour tout entier naturel n, T_n=20+160\times 0.955n .

correction

c. Calculer la limite de la suite (T_n).

correction

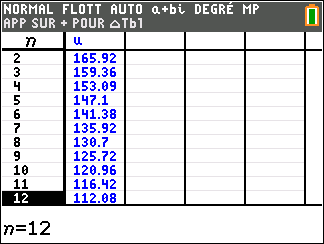
d. Résoudre l’inéquation T_n\leq 120 d’inconnue n entier naturel.

conjecture avec la TI 83
correction

3. Dans cette partie, on s’intéresse à l’évolution de la température au centre d’un gâteau après sa sortie du four.
On considère qu’à la sortie du four, la température au centre du gâteau est de 180° C et celle de l’air ambiant de 20° C.
La loi de refroidissement de Newton permet de modéliser la température au centre du gâteau par la suite précédente (T_n). Plus précisément, T_n représente la température au centre du gâteau, exprimée en degré Celsius, n minutes après sa sortie du four.
a. Expliquer pourquoi la limite de la suite (T_n) déterminée à la question 2. c. était prévisible dans le contexte de l’exercice.

correction

b. On considère la fonction Python ci-dessous :

Donner le résultat obtenu en exécutant la commande temp(120).
Interpréter le résultat dans le contexte de l’exercice.

correction

©2020 – Math’O karé SAS

On considère la suite (T_n) définie par :
T_0=180 et, pour tout entier naturel n, T_{n+1}=0.955T_n+0.9
On veut montrer par récurrence que pour tout entier naturel n, T_n\geq 20.

Initialisation : J’écris la propriété au premier rang en remplaçant tous les n par 0.

T_0\geq 120 vraie car T_0=180

Transmission ou hérédité : .

T_n\geq 20\\0.955T_n\geq 0.955\times 20\\0.955T_n\geq 19.1\\0.955T_n+0.9\geq 19.1+0.9\\0.955T_n+0.9\geq 20\\T_{n+1}\geq 20

étape n°1 : j’écris la propriété au rang  n en haut.

étape n°4 : Je multiplie par 0.955 l’inégalité, le sens  ne change pas car 0.955 est positif.

étape n°5 : Je calcule.

étape n°6 : J’ajoute 0.9 aux deux membres de l’inégalité.

étape n°3 : je remplace  T_{n+1} par 0.955 T_n+0.9.

étape n°2 : j’écris la propriété au rang n+1 en bas.

Conclusion : J’écris la propriété au rang  n et je rajoute pour tout n.

Pour tout entier naturel n, T_n\geq 20.

 

On veut vérifier que pour tout entier naturel n, T_{n+1}-T_n=-0.045(T_n-20). En déduire le sens de variation de la suite (T_n).

T_{n+1}-T_n=0.955T_n+0.9-T_n\\T_{n+1}-T_n=-0.045T_n+0.9\\T_{n+1}-T_n=-0.045\times T_n+0.045\times 20\\T_{n+1}-T_n=-0.045(T_n-20)

étape n°1 : On remplace T_{n+1} par 0.955T_n+0.9

étape n°4 : On calcule

étape n°3 : On développe -0.045( T_n-20).

étape n°2 : on écrit la conclusion en bas.

On a montré par récurrence que T_n\geq 20 donc T_n-20 est positif donc  -0.045(T_n-20) est négatif donc T_{n+1}-T_n est négatif donc la suite (T_n) est décroissante.

 

La suite (T_n) est  décroissante et minorée par 20. Donc d’après le théorème de convergence monotone, la suite (T_n) converge.

u_n=T_n-20.
Pour montrer que la suite (u_n) est géométrique, nous allons prouver l’égalité suivante u_{n+1}=q\times u_n.

On part du premier membre u_{n+1}, on le transforme pour arriver au second membre q\times u_n.

u_{n+1}=T_{n+1}-20 

\hspace{0.75cm}=0.955T_n+0.9-20. 

\hspace{0.75cm}=0.955T_n-19.1 

\hspace{0.75cm}=0.955(T_n-20)

\hspace{0.75cm}=0.955\times u_n

Etape n°1 : On exprime u_{n+1} en fonction de T_{n+1}

Etape n°4 : On exprime T_{n+1} en fonction de T_{n}

Etape n°5 :  On réduit la somme. En mettant en facteur le coefficient par lequel T_n est multiplié , ici 0.955, on arrivera à l’étape n°3.

Etape n°3 :  On remplace u_n par T_n-20

Etape n°2 :  On écrit le second membre de l’égalité qu’on veut démontrer.

Donc la suite (u_n) est géométrique de raison 0.955.

Pour calculer v_0, on remplace n par 0 dans v_n=u_n-2500.

v_0=u_0-2500

On remplace u_0 par 1000.

v_0=1000-2500

v_0=-1500

On veut montrer que T_n=20+160\times 0.955n .

1.On va utiliser l’égalité u_n=T_n-20 pour trouver une expression de T_n.

u_n=T_n-20

A=B et B=A sont des égalités équivalentes.

T_n-20=u_n

-20 n’est pas à sa place, j’ajoute 20 de chaque côté.

T_n=u_n+20

2.On va exprimer  u_n en fonction de n.

On a montré que la suite (u_n) est géométrique de raison 0.955

On calcule le premier terme u_0=T_0-20=180-20=160.

Donc u_n=160\times 0.955^n

3.On conclut

On remplace u_n par 160\times 0.955^n dans T_n=u_n+20.

T_n=160\times 0.955^n+20

T_n=20+160\times 0.955^n.

Comme -1<0.955<1 on a : lim_{n\to+\infty}\hspace{0.2cm}160\times 0.955^n=0

Donc lim_{n\to+\infty}\hspace{0.2cm}T_n=20

Taper sur la touche mode et sélectionner SUITE sur la 5ème ligne. Puis quitter avec 2nde mode

Taper ensuite sur la touche f(x) en haut à gauche. Comme la suite  est définie par formule explicite, à l’aide des flèches, dans TYPE sélectionner SUITE(n+1).

On programme la suite

Pour cela sur la ligne nMin saisir  le plus petit rang, c’est souvent 0 mais il arrive que ce soit 1 ou autre chose. 

Puis compléter la ligne u(n+1)=. Pour saisir n taper au clavier sur la touche X,T,O,n et pour saisir u taper sur la touche 2nde puis sur la touche 7.

Compléter la ligne u(0)=

Pour afficher les termes de la suite, s’assurer que le tableur est bien paramétré, faire 2nde puis fenêtre on doit avoir 0, 1, AUTO et AUTO.

Taper sur la touche 2nde et sur la touche graphe, le tableur apparaît.

On descend dans le tableau et on voit que les termes de la suite sont inférieurs à 120 à partir du rang 11

On va résoudre T_n\leq 120.

C’est-à-dire

160\times 0.955^n+20\leq 120

20 n’est pas à sa place, on enlève 20 de chaque côté

160\times 0.955^n\leq 120-20

160\times 0.955^n\leq 100

160 n’est pas à sa place, c’est un facteur dans un produit, on divise par 160 de chaque côté.

0.955^n\leq \frac{100}{160}

0.955^n\leq \frac{5}{8}

On va utiliser la fonction logarithme népérien. Comme elle est croissante, les nombres et les images varient dans le même sens.

ln(0.955^n)\leq ln(\frac{5}{8})

On utilise la propriété ln(a^n)=n\times ln(a)

n\times ln(0.955)\leq ln(\frac{5}{8})

ln(0.955) n’est pas à sa place, c’est un facteur dans un produit, on divise par ln(0.955) de chaque côté. Comme 0.955<1, ln(0.955) est négatif le sens de l’inégalité change.

n\geq \frac{ln(\frac{5}{8})}{ln(0.955)}

Après calcul à la calculatrice.

n\geq 10.21

Donc à partir du rang 11, T_n\leq 120.

Lorsque le gâteau est sorti du four, il va céder son énergie (sa chaleur) à l’extérieur (environnement ambiant). Sa masse étant très faible par rapport à celle de l’extérieur, il va diminuer sa température pour atteindre celle de l’extérieur, soit 20° C. ce qui correspond au résultat précédent à savoir : lim_{n\to+\infty}\hspace{0.2cm}T_n=20

 La fonction Python décrite est un algorithme de seuil : on cherche à partir de quand, la température devient inférieure ou égale au seuil fixé (ici l’argument de la fonction seuil() qui est x). La valeur renvoyée sera le premier entier vérifiant T_n \leq x.
temp(120) fournira le premier nombre entier n tel que T_n \leq 120, soit d’après la question précédente, n=11. Dans le contexte de l’exercice, il faudra donc 11 minutes avant que la température du plat soit inférieure ou égale à 120° C.

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.