T. bac2022 suites exo n°5 ( Polynésie 30 Août 2022 )

ANALYSE, Exercices bac 2022 : les suites, Niveau terminale spécialité

Soit $k$ un nombre réel.
On considère la suite $(u_n)$ définie par son premier terme $u_0$ et pour tout entier naturel $n$ , $u_{n+1}=ku_n(1-u_n)$ .
Les deux parties de cet exercice sont indépendantes.
On y étudie deux cas de figure selon les valeurs de $k$ .

Partie 1
Dans cette partie, $k=1.9$ et $u_0=0.1$ .
On a donc, pour tout entier naturel $n$ , $u_{n+1}=1.9u_n(1-u_n)$ .
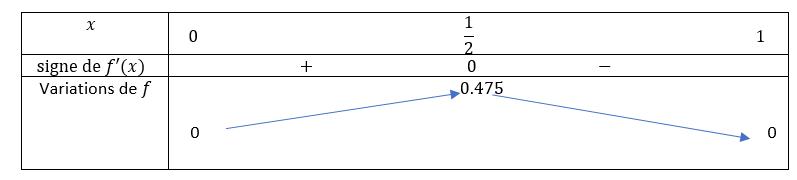
1. On considère la fonction $f$ définie sur $[0;1]$ par $f(x)=1.9x(1-x)$ .
a. Étudier les variations de $f$ sur $[0;1]$ .

b. En déduire que si $x \in [0;1]$ alors $f(x) \in [0;1]$ .

2. Ci-dessous sont représentés les premiers termes de la suite $(u_n)$ construits à partir de la courbe $C_f$ de la fonction $f$ et de la droite $D$ d’équation $y=x$ .

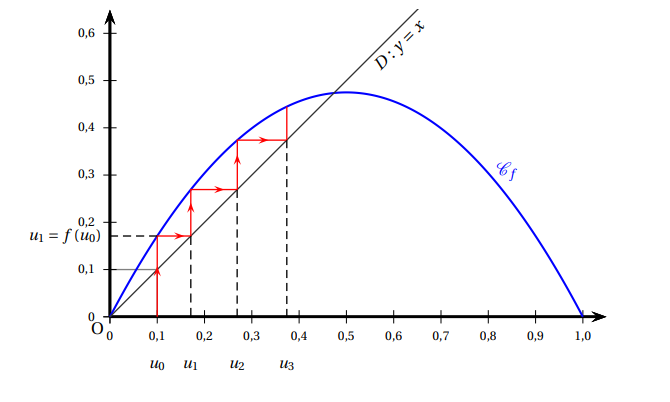
Conjecturer le sens de variation de la suite $(u_n)$ et sa limite éventuelle.

3. a. En utilisant les résultats de la question 1, démontrer par récurrence que pour tout entier naturel $n$ :
$0\leq u_n\leq u_{n+1}\leq \frac{1}{2}$ .

b. En déduire que la suite $(u_n)$ converge.

c. Déterminer sa limite.

Partie 2

Dans cette partie, $k=\frac{1}{2}$ et $u_0=\frac{1}{4}$
On a donc, pour tout entier naturel $n$ , $u_{n+1}=\frac{1}{2}u_n(1-u_n)$ et $u_0=\frac{1}{4}$ .
On admet que pour tout entier naturel $n$ : $0\leq u_n \leq (\frac{1}{2})^n$ .

1. Démontrer que la suite $(u_n)$ converge et déterminer sa limite.

2. On considère la fonction Python algo (p) où $p$ désigne un entier naturel non nul :

Expliquer pourquoi, pour tout entier naturel non nul $p$ , la boucle while ne tourne pas indéfiniment, ce qui permet à la commande algo (p) de renvoyer une valeur.

$f(x)$ est	$f'(x)$ se calcule ainsi :
une somme $u+v$	$u’+v’$
le produit d’une constante $k$ par une fonction $u$ c’est-à-dire $ku$	$k\times u’$
un produit de deux fonctions $u\times v$	$u’\times v+u\times v’$
l’inverse d’une fonction $\frac{1}{u}$	$-\frac{u’}{u^2}$
un quotient $\frac{u}{v}$	$\frac{u’\times v-u\times v’}{v^2}$

Fonction	Dérivée
$v\circ u$	$(v’\circ u)\times u’$
$u^2$	$2u’u$
$u^3$	$3u’u^2$
$u^n$	$nu’u^{n-1}$
$\frac{1}{u}$	$-\frac{u’}{u^2}$
$\sqrt{u}$	$\frac{u’}{2\sqrt{u}}$
$cos(u)$	$-u’sin(u)$
$sin(u)$	$u’cos(u)$
$e^{u}$	$u’e^{u}$
$ln(u)$	$\frac{u’}{u}$
$\frac{1}{u^{n}}$	$-\frac{nu’}{u^{n+1}}$

Fonction	$f(x)$	Dérivable sur	$f'(x)$
constante	$f(x)=k$	$\mathbf{R}$	$f'(x)=0$
identité	$f(x)=x$	$\mathbf{R}$	$f'(x)=1$
carré	$f(x)=x^2$	$\mathbf{R}$	$f'(x)=2x$
cube	$f(x)=x^3$	$\mathbf{R}$	$f'(x)=3x^2$
puissance n	$f(x)=x^n$	$\mathbf{R}$	$f'(x)=nx^{n-1}$
inverse	$f(x)=\frac{1}{x}$	$\left]-\infty;0\right[\cup\left]0;+\infty\right[$	$f'(x)=-\frac{1}{x^2}$
racine carrée	$f(x)=\sqrt{x}$	$]0;+\infty[$	$f'(x)=\frac{1}{2\sqrt{x}}$
exponentielle	$f(x)=e^x$	$\mathbf{R}$	$f'(x)=e^x$
sinus	$f(x)=sin(x)$	$\mathbf{R}$	$f'(x)=cos(x)$
cosinus	$f(x)=cos(x)$	$\mathbf{R}$	$f'(x)=-sin(x)$
logarithme népérien	$f(x)=ln(x)$	$]0;+\infty[$	$f'(x)=\frac{1}{x}$

T. bac2022 suites exo n°5 ( Polynésie 30 Août 2022 )

Dérivées et opérations

Dérivées et fonctions composées

Dérivées des fonctions de référence