logo

T. bac2023 probabilités exo n°1 ( Métropole 20 Mars 2023 )

Cet exercice est un questionnaire à choix multiple.
Pour chaque question, une seule des quatre réponses proposées est exacte.
Le candidat indiquera sur sa copie le numéro de la question et la réponse choisie.
Aucune justification n’est demandée.
Aucun point n’est enlevé en l’absence de réponse ou en cas de réponse inexacte.
Les questions sont indépendantes.
Un technicien contrôle les machines équipant une grande entreprise. Toutes ces machines sont identiques.
On sait que :
• 20 % des machines sont sous garantie;
• 0.2 % des machines sont à la fois défectueuses et sous garantie;
• 8.2 % des machines sont défectueuses.
Le technicien teste une machine au hasard.
On considère les évènements suivants :
• G : « la machine est sous garantie »;
• D : « la machine est défectueuse »;
• \overline{G} et \overline{D} désignent respectivement les évènements contraires de G et D.
Pour répondre aux questions 1 à 3, on pourra s’aider de l’arbre proposé ci-contre.

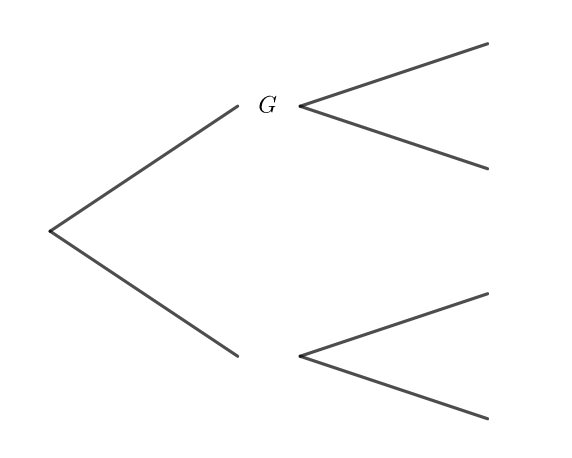
1. La probabilité p_G(D) de l’évènement D sachant que G est réalisé est égale à :

a. 0.002

b. 0.01

c. 0.024

d. 0.2

correction

2. La probabilité p(\overline{G}\cap D) est égale à :

a. 0.01

b. 0.08

c. 0.1

d. 0.21

correction

3. La machine est défectueuse. La probabilité qu’elle soit sous garantie est environ égale, à  10^{-3} près à :

a. 0.01

b. 0.08

c. 0.1

d. 0.21

correction

Pour les questions 4 et 5, on choisit au hasard et de façon indépendante n machines de l’entreprise, où n désigne un entier naturel non nul.
On assimile ce choix à un tirage avec remise, et on désigne par X la variable aléatoire qui associe à chaque lot de n machines le nombre de machines défectueuses dans ce lot.
On admet que X suit la loi binomiale de paramètres n et p=0.082.

4. Dans cette question, on prend n=50.
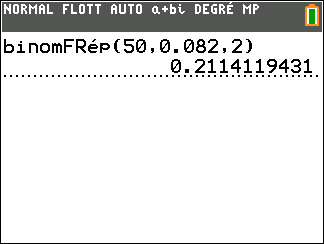
La valeur de la probabilité p(X>2), arrondie au millième, est de :

a. 0.136

b. 0.789

c. 0.864

d. 0.924

correction

5. On considère un entier n pour lequel la probabilité que toutes les machines d’un lot de taille n fonctionnent correctement est supérieure à 0.4.
La plus grande valeur possible pour n est égale à : 

a. 5

b. 6

c. 10

d. 11

correction

©2020 – Math’O karé SAS

Compte-tenu des données de l’énoncé, mieux vaut utiliser la formule p_{G}(D)=\frac{p(G\cap D)}{p(G)} plutôt que d’utiliser l’arbre.
• 20 % des machines sont sous garantie donc p(G)=0.20
• 0.2 % des machines sont à la fois défectueuses et sous garantie donc p(G\cap D)=0.002.
On remplace p(G) par 0.20 et p(G\cap D) par 0.002  dans la formule p_{G}(D)=\frac{p(G\cap D)}{p(G)}.

p_{G}(D)=\frac{0.002}{0.2}=0.01.

La bonne réponse est la réponse b.

La probabilité p(\overline{G}\cap D) est égale à :

Compte-tenu des données de l’énoncé, mieux vaut utiliser la formule des probabilités totales

p(G\cap D)+p(\overline{G}\cap D)=p(D).
On sait que  p(D)=0.082
On sait que p(G\cap D)=0.002.

On remplace p(D) par 0.082 et p(G\cap D) par 0.002  dans la formule des probabilités totales

p(G\cap D)+p(\overline{G}\cap D)=p(D)

0.002+p(\overline{G}\cap D)=0.082

Donc p(\overline{G}\cap D)=0.082-0.002=0.08.

La bonne réponse est la réponse b.

La machine est défectueuse. La probabilité qu’elle soit sous garantie est environ égale, à  10^{-3} près à :

On reformule la question : sachant que la machine est défectueuse, la probabilité qu’elle soit sous garantie est environ égale, à  10^{-3} près à :

Compte-tenu des données de l’énoncé, mieux vaut utiliser la formule p_{D}(G)=\frac{p(G\cap D)}{p(D)} plutôt que d’utiliser l’arbre.
On sait que   p(D)=0.082
On sait que p(G\cap D)=0.002.
On remplace p(D) par 0.082 et p(G\cap D) par 0.002  dans la formule p_{D}(G)=\frac{p(G\cap D)}{p(D)}.

p_{D}(G)=\frac{0.002}{0.082}=0.024.

La bonne réponse est la réponse b.

On veut calculer p(X>2) arrondie à 10^{-3} près.

p(X> 2)=1-p(X\leq 2)=1-0.211=0.789.

La bonne réponse est la réponse b.

On a obtenu le résultat p(X\leq 2)=0.211 avec la calculatrice TI 83 Premium CE de la manière suivante :

Au clavier

A l’écran

Taper sur la touche 2nde puis sur la touche var. Dans le menu déroulant, on sélectionne la ligne

B:binomFRép(

On valide avec entrer

Sur la ligne NbreEssais, on saisit le nombre de répétitions c’est-à-dire n.

Sur la ligne p, on saisit la probabilité du succès.

Sur la ligne valeur de x, on saisit le nombre de succès souhaité.

Faire entrer deux fois.

 

 

On veut déterminer la plus grande valeur de l’entier n pour laquelle la probabilité que toutes les machines fonctionnent correctement est supérieure à 0.4.

On cherche donc pour quelles valeurs de n, p(X=0)>0.4.

\binom{10}{0}0.082^{0}(1-0.082)^n> 0.4\\0.918^{n}>0.4\\ln(0.918^{n})< ln(0.4)\\n\times  ln(0.918)> ln(0.4)

On divise par ln(0.918) qui est négatif donc l’inégalité change de sens.

n <\frac{ln(0.4)}{ln(0.918)}\\n < 10.71

Il faut donc  au moins 10 machines pour que la probabilité que toutes les machines fonctionnent correctement soit supérieure à 0.4.

La bonne réponse est la réponse c.

 

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.