Les deux parties de cet exercice sont indépendantes.
Dans une grande ville française, des trottinettes électriques sont mises à disposition des usagers. Une
entreprise, chargée de l’entretien du parc de trottinettes, contrôle leur état chaque lundi.
Partie A
On estime que :
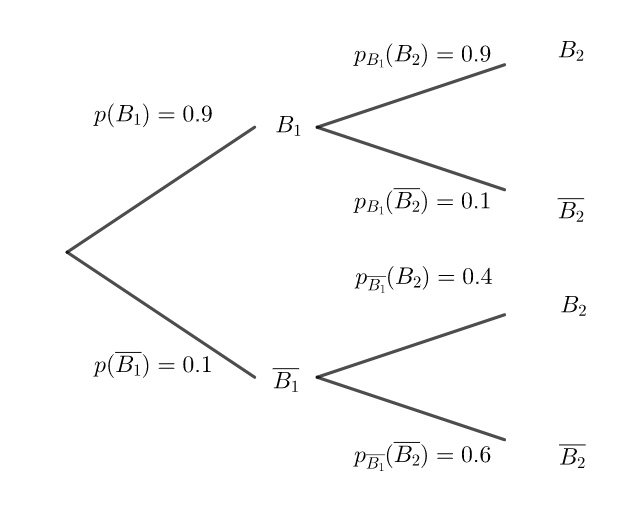
— lorsqu’une trottinette est en bon état un lundi, la probabilité qu’elle soit encore en bon état le lundi suivant est 0.9;
— lorsqu’une trottinette est en mauvais état un lundi, la probabilité qu’elle soit en bon état le lundi suivant est 0.4.
On s’intéresse à l’état d’une trottinette lors des phases de contrôle.
Soit n un entier naturel. On note B_n l’évènement « la trottinette est en bon état n semaines après sa mise en service » et p_n la probabilité de B_n.
Lors de sa mise en service, la trottinette est en bon état. On a donc p_0=1.
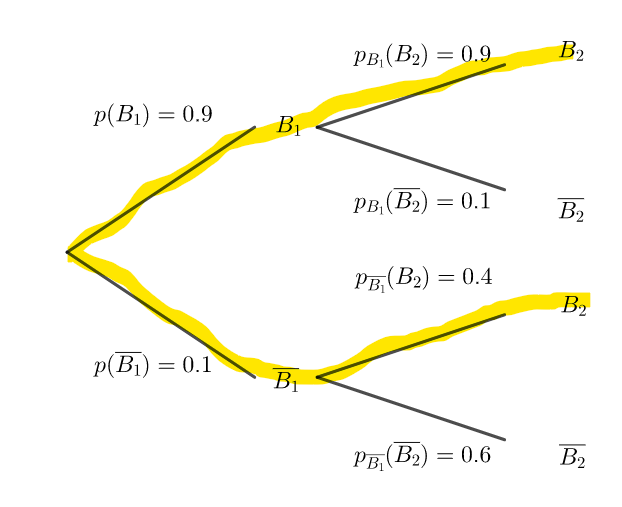
1. Donner p_1 et montrer que p_2=0.85.
On pourra s’appuyer sur un arbre pondéré.
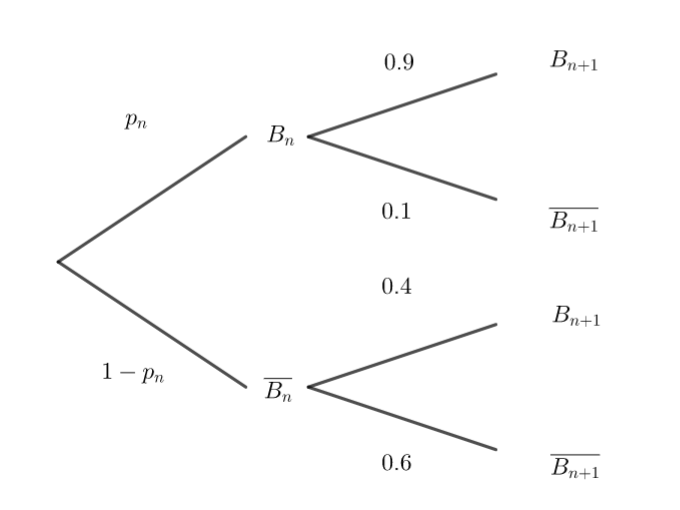
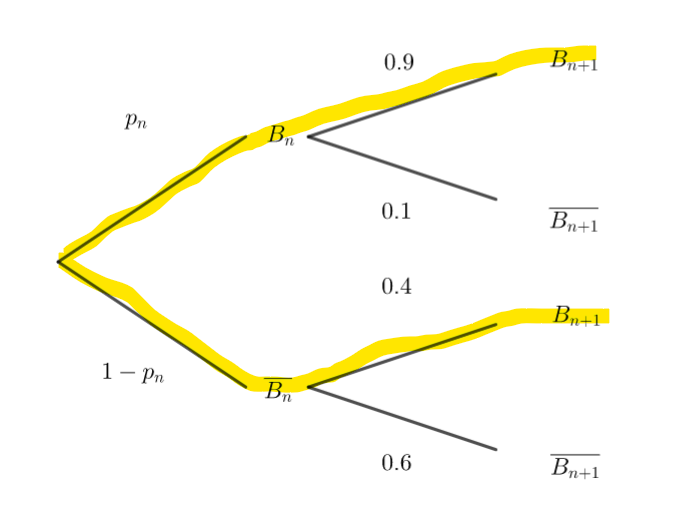
2. Recopier et compléter l’arbre pondéré ci-dessous :
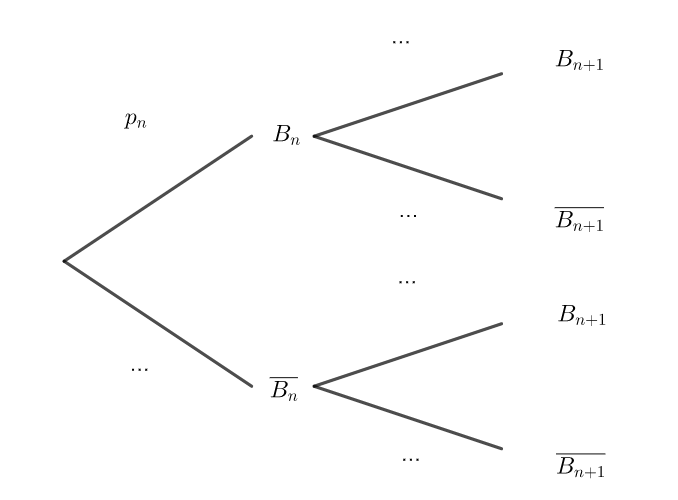
3. En déduire que, pour tout entier naturel n,
p_{n+1}=0.5p_n+0.4.
4. a. Démontrer par récurrence que pour tout entier naturel n,
p_{n}>0.8.
b. À partir de ce résultat, quelle communication l’entreprise peut-elle envisager pour valoriser la fiabilité du parc ?
5. a. On considère la suite (u_{n}) définie pour tout entier naturel n par u_{n}=p_n-0.8.
Montrer que (u_{n}) est une suite géométrique dont on donnera le premier terme et la raison.
b. En déduire l’expression de u_{n} puis de p_{n} en fonction de n.
c. En déduire la limite de la suite (p_{n}).
Partie B
Dans cette partie, on modélise la situation de la façon suivante :
— l’état d’une trottinette est indépendant de celui des autres;
— la probabilité qu’une trottinette soit en bon état est égale à 0.8.
On note X la variable aléatoire qui, à un lot de 15 trottinettes, associe le nombre de trottinettes en bon état.
Le nombre de trottinettes du parc étant très important, le prélèvement de 15 trottinettes peut être assimilé à un tirage avec remise.
1. Justifier que X suit une loi binomiale et préciser les paramètres de cette loi.
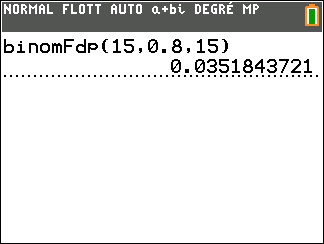
2. Calculer la probabilité que les 15 trottinettes soient en bon état.
3. Calculer la probabilité qu’au moins 10 trottinettes soient en bon état dans un lot de 15.
4. On admet que E(X)=12. Interpréter le résultat.