Les parties A et B peuvent être traitées indépendamment
Les utilisateurs de vélo d’une ville sont classés en deux catégories disjointes :
• ceux qui utilisent le vélo dans leurs déplacements professionnels;
• ceux qui utilisent le vélo uniquement pour leurs loisirs.
Un sondage donne les résultats suivants :
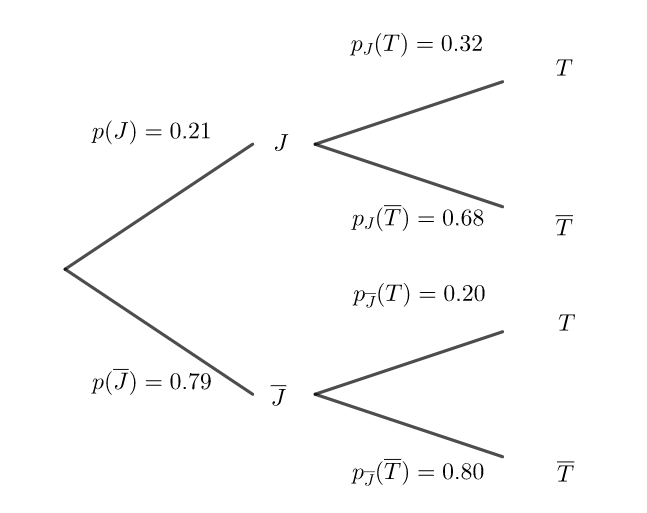
• 21 % des utilisateurs ont moins de 35 ans.
Parmi eux, 68 % utilisent leur vélo uniquement pour leurs loisirs alors que les autres l’utilisent dans leurs déplacements professionnels;
• parmi les 35 ans ou plus, seuls 20 % utilisent leur vélo dans leurs déplacements professionnels, les autres l’utilisent uniquement pour leurs loisirs.
On interroge au hasard un utilisateur de vélo de cette ville.
Dans tout l’exercice on considère les évènements suivants :
• J : « la personne interrogée a moins de 35 ans »;
• T : « la personne interrogée utilise le vélo dans ses déplacements professionnels »;
• \overline{J} et \overline{T} sont les évènements contraires de J et T .
Partie A
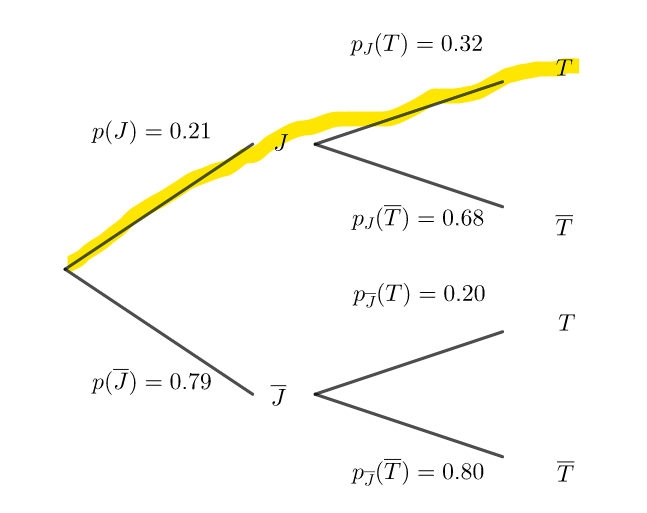
1. Calculer la probabilité que la personne interrogée ait moins de 35 ans et utilise son vélo dans ses déplacements professionnels.
On pourra s’appuyer sur un arbre pondéré.
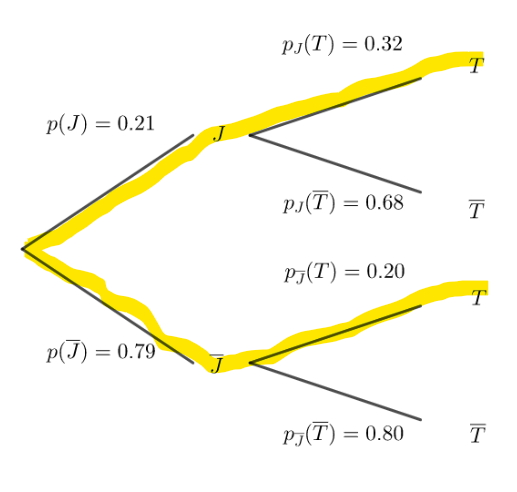
2. Calculer la valeur exacte de la probabilité de T.
3. On considère à présent un habitant qui utilise son vélo dans ses déplacements professionnels.
Démontrer que la probabilité qu’il ait moins de 35 ans est 0.30 à 10^{-2} près.
Partie B
Dans cette partie, on s’intéresse uniquement aux personnes utilisant leur vélo dans leurs déplacements professionnels.
On admet que 30 % d’entre elles ont moins de 35 ans.
On sélectionne au hasard parmi elles un échantillon de 120 personnes auxquelles on va soumettre un questionnaire supplémentaire.
On assimile la sélection de cet échantillon à un tirage aléatoire avec remise.
On demande à chaque individu de cet échantillon son âge.
X représente le nombre de personnes de l’échantillon ayant moins de 35 ans.
Dans cette partie, les résultats seront arrondis à 10^{-3} près.
1. Déterminer la nature et les paramètres de la loi de probabilité suivie par X.
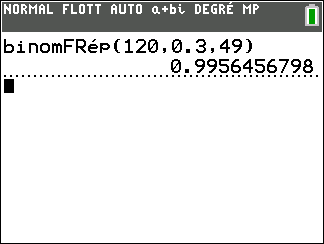
2. Calculer la probabilité qu’au moins 50 utilisateurs de vélo parmi les 120 aient moins de 35 ans.