Une entreprise appelle des personnes par téléphone pour leur vendre un produit.
— L’entreprise appelle chaque personne une première fois :
• la probabilité que la personne ne décroche pas est égale à 0.6;
• si la personne décroche, la probabilité qu’elle achète le produit est égale à 0.3.
— Si la personne n’a pas décroché au premier appel, on procède à un second appel :
• la probabilité que la personne ne décroche pas est égale à 0.3;;
• si la personne décroche, la probabilité qu’elle achète le produit est égale à 0.2.
— Si une personne ne décroche pas au second appel, on cesse de la contacter.
On choisit une personne au hasard et on considère les évènements suivants :
D_1 : « la personne décroche au premier appel »;
D_2; : « la personne décroche au deuxième appel »;
A : « la personne achète le produit ».
Les deux parties peuvent être traitées de manière indépendante
Partie A
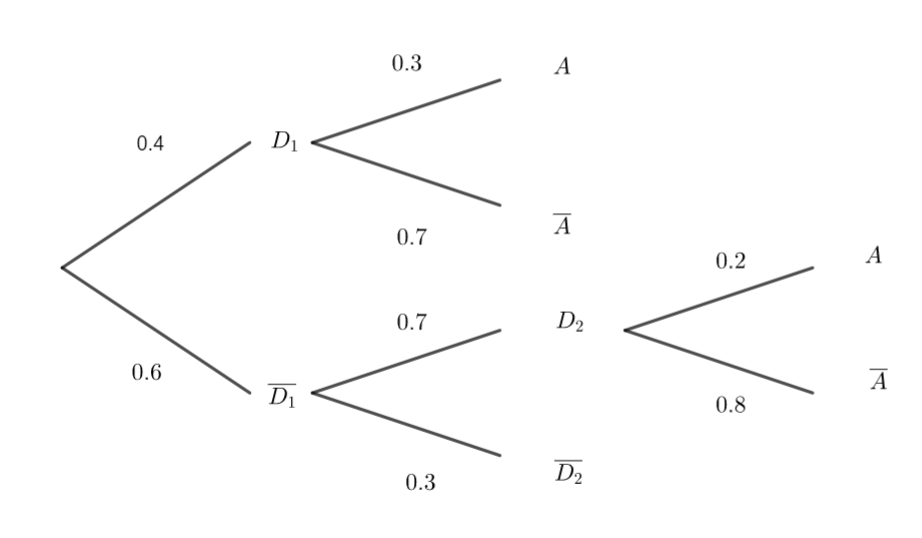
1. Recopier et compléter l’arbre pondéré cicontre.
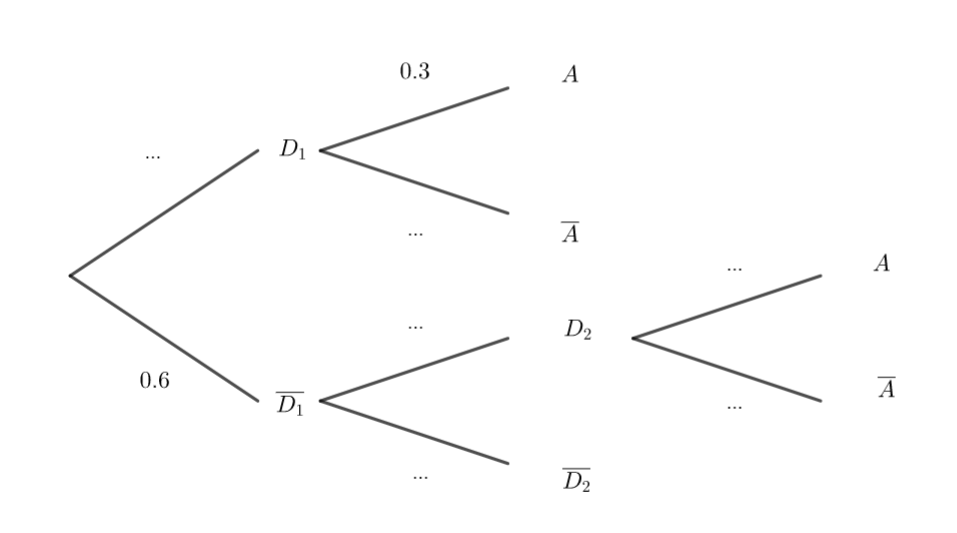
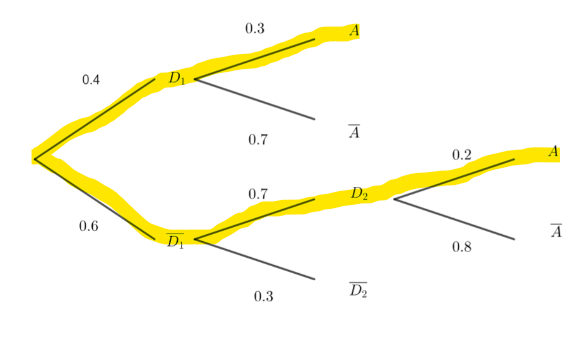
2. En utilisant l’arbre pondéré, montrer que la probabilité de l’évènement A est
p(A)=0.204.
3. On sait que la personne a acheté le produit. Quelle est la probabilité qu’elle ait décroché au premier appel ?
Partie B
On rappelle que, pour une personne donnée, la probabilité qu’elle achète le produit est égale à 0.204.
1. On considère un échantillon aléatoire de 30 personnes.
On note X la variable aléatoire qui donne le nombre de personnes de l’échantillon qui achètent le produit.
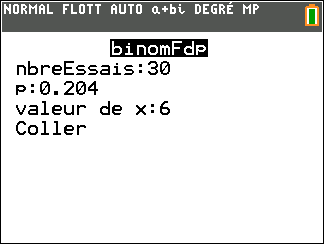
a. On admet que X suit une loi binomiale. Donner, sans justifier, ses paramètres.
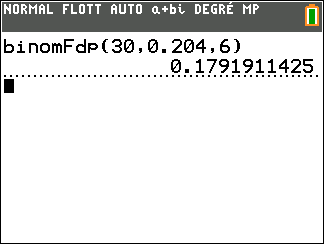
b. Déterminer la probabilité qu’exactement 6 personnes de l’échantillon achètent le produit.
Arrondir le résultat au millième.
c. Calculer l’espérance de la variable aléatoire X.
Interpréter le résultat.
2. Soit n un entier naturel non nul.
On considère désormais un échantillon de n personnes.
Déterminer la plus petite valeur de n telle que la probabilité qu’au moins l’une des personnes de l’échantillon achète le produit soit supérieure ou égale à 0.99.