Dans un souci de préservation de l’environnement, Monsieur Durand décide de se rendre chaque matin au travail en utilisant son vélo ou les transports en commun.
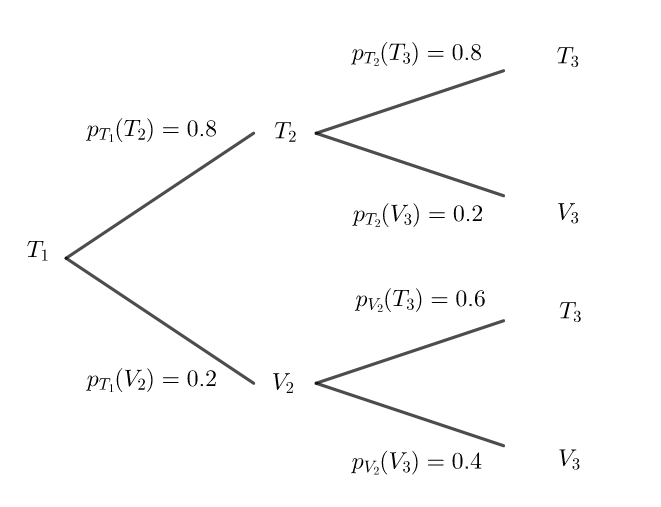
S’il choisit de prendre les transports en commun un matin, il reprend les transports en commun le lendemain avec une probabilité égale à 0.8.
S’il utilise son vélo un matin, il reprend son vélo le lendemain avec une probabilité égale à 0.4.
Pour tout entier naturel n non nul, on note :
• T_n l’évènement « Monsieur Durand utilise les transports en commun le n-ième jour »
• Vn l’évènement « Monsieur Durand utilise son vélo le n-ième jour »
• On note p_n la probabilité de l’évènement T_n,
Le premier matin, il décide d’utiliser les transports en commun. Ainsi, la probabilité de l’évènement
T_1 est p_1=1.
1. Recopier et compléter l’arbre pondéré ci-dessous représentant la situation pour les 2^{ème} et 3^{ème} jours,
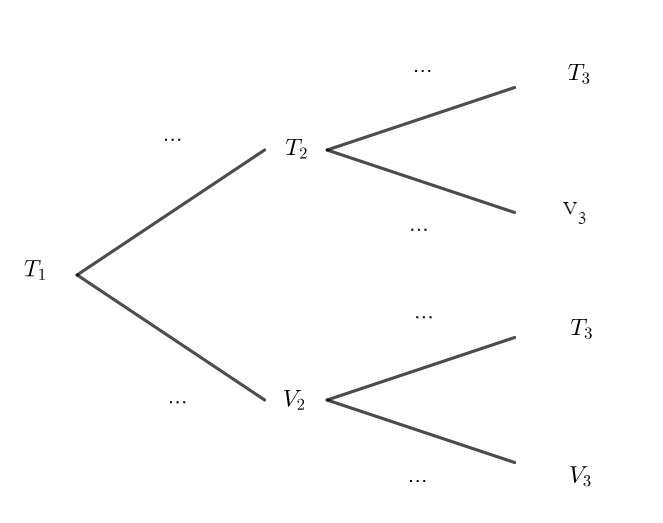
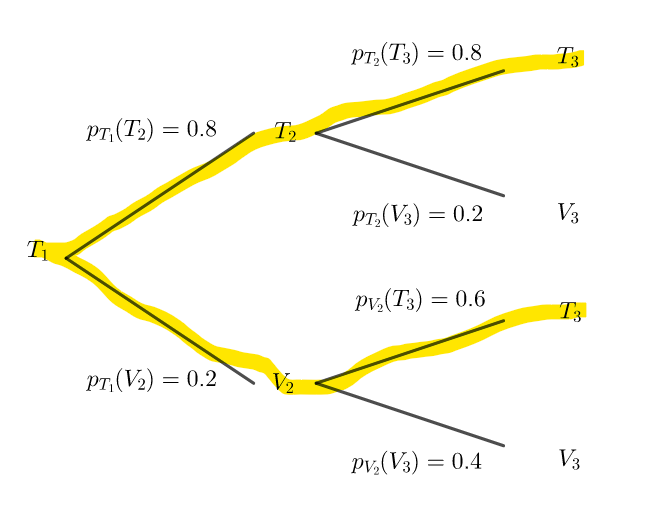
2. Calculer p_3.
3. Le 3^{ème} jour, M. Durand utilise son vélo.
Calculer la probabilité qu’il ait pris les transports en commun la veille.
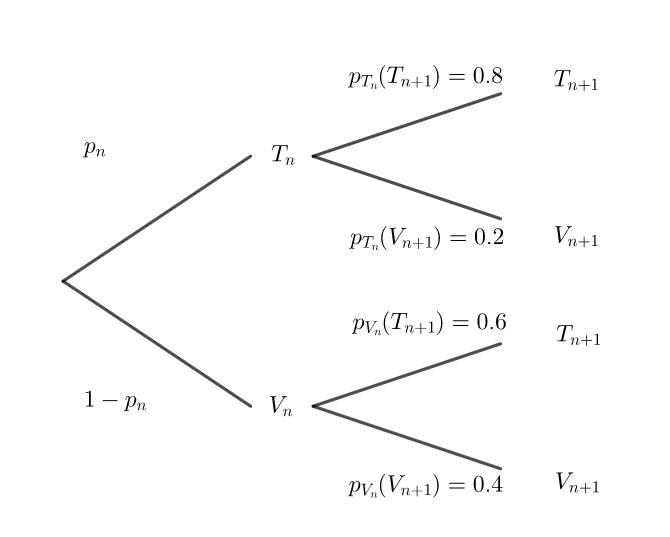
4. Recopier et compléter l’arbre pondéré ci-dessous représentant la situation pour les n^{ième} et n+1^{ième} jours.
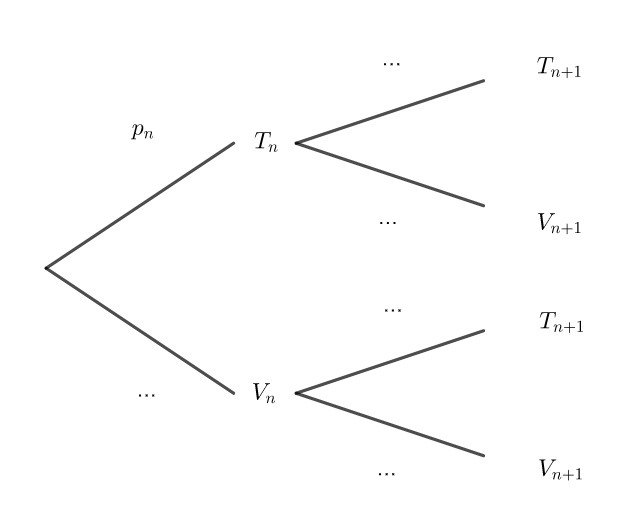
5. Montrer que, pour tout entier naturel n non nul,
p_{n+1}=0.2p_n+0.6.
6. Montrer par récurrence que, pour tout entier naturel n non nul, on a
p_{n}=0.75+0.25\times 0.2^{n-1}.
7. Déterminer la limite de la suite (p_{n}) et interpréter le résultat dans le contexte de l’exercice.