Lorsqu’on a identifié qu’on va utiliser a^{2}-2ab +b^{2}= (a-b)^{2} pour factoriser.
Le plus simple est d’abord de compléter les pointillés ci-dessous:
a^{2}=… donc a=…\\b^{2}=… donc b=…
Ensuite je calcule le double produit 2ab en remplaçant a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ.
Pour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :
a^{2}-2ab +b^{2}= (a-b)^{2}Factorisons par exemple, 9x^{2}-12x+4.
1. Ce qu’il doit y avoir sur la copie :
a^{2}=9x^2 donc a=3x\\b^{2}=4 donc b=2
Ensuite je calcule le double produit 2ab en remplaçant a et b par leurs valeurs et je m’assure que le résultat obtenu est bien le troisième terme de l’expression de départ.
2ab=2\times 3x\times 2=12xPour finir, il suffit de remplacer a, b , a^{2}, 2ab et b^{2} par leurs valeurs dans :
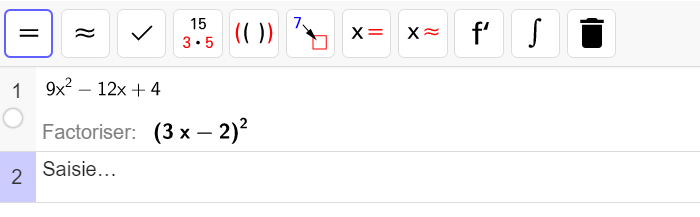
9x^2-12x+4= (3x-2)^{2}2. Valider notre réponse à l’aide de l’application Calcul Formel de géogébra.