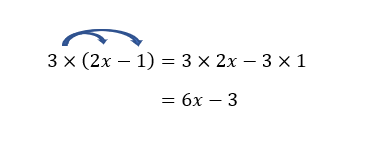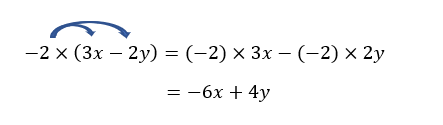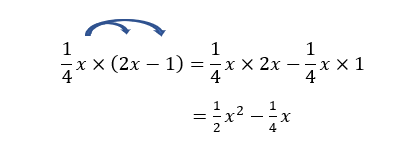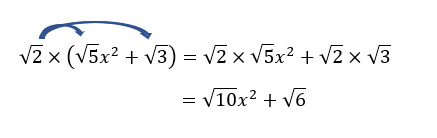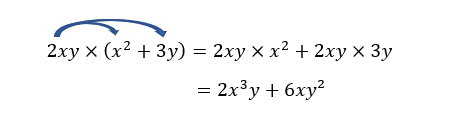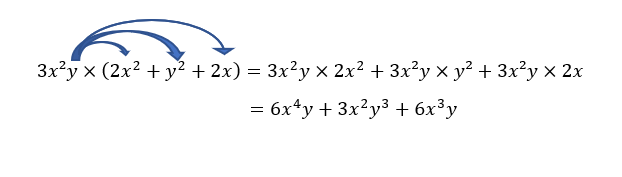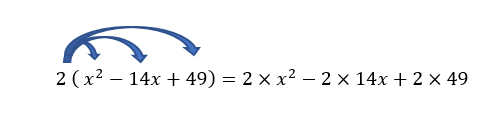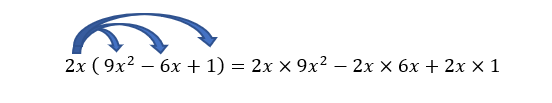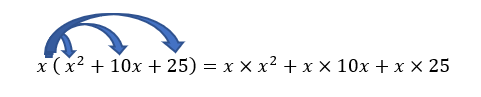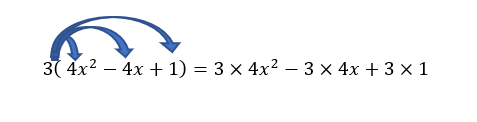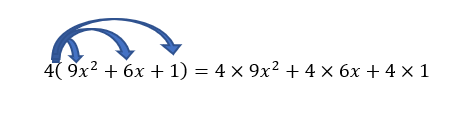logo

2.Développer.Exercices.

Sommaire

Exercice n°1

Développer, dans chaque cas, à l’aide de la distributivité de la multiplication par rapport à l’addition. Valider votre réponse avec la page Calcul formel de Géogébra située à la fin de l’exercice.

  1. 3(2x-1)
correction

2. -2(3x-2y)

correction

3. \frac{1}{4}x(2x-1)

correction

4. \sqrt{2}(\sqrt{5}x^2+\sqrt{3})

correction

5. 2xy(x^2+3y)

correction

6. 3x^2y(2x^2+y^2+2x)

correction

Exercice n°2 

Développer, dans chaque cas, à l’aide de l’identité (a+b)^2=a^2+2ab+b^2. Valider ]votre réponse avec la page Calcul formel de Géogébra située à la fin de l’exercice.

  1. (3x+5)^2.
correction

2. (2x+7)^2.

correction

3. (6x+\frac{2}{5})^2.

correction

4. (x+\sqrt{2})^2.

correction

5. (\frac{1}{2}x+\frac{1}{3})^2.

correction

Exercice n°3 

Développer, dans chaque cas, à l’aide de l’identité (a-b)^2=a^2-2ab+b^2. Valider votre réponse avec la page Calcul formel de Géogébra située à la fin de l’exercice.

  1. (2x-7)^2.
correction

2. (x-\sqrt{3})^2.

correction

3. (\frac{1}{2}x-5)^2.

correction

4. (4x-\frac{1}{3})^2.

correction

5. (\frac{1}{4}x-\frac{1}{2})^2.

correction

Exercice n°4

Développer, dans chaque cas, à l’aide de l’identité (a-b)(a+b)=a^2-b^2. Valider ]votre réponse avec la page Calcul formel de Géogébra située à la fin de l’exercice.

  1. (x-5)(x+5).
correction

2. (2x-3)(2x+3).

correction

3. (x-\sqrt{2})(x+\sqrt{2}).

correction

4. (\frac{1}{5}x-4)(\frac{1}{5}x+4).

correction

5. (\frac{1}{7}x-\frac{1}{5})(\frac{1}{7}x+\frac{1}{5}).

correction

Exercice n°5 

Dans chaque cas, déterminer la forme développée et réduite de l’expression proposée. Valider votre réponse avec la page Calcul formel de Géogébra située à la fin de l’exercice.

  1. 2(x-7)^2.
correction

2. 2x(3x-1)^2.

correction

3. x(x+5)^2+3x.

correction

4. 3(2x-1)^2+1.

correction

5. 4(3x+1)^2-10.

correction

Page Géogébra pour valider.

Sur la ligne 1, saisir l’expression à développer.

Puis cliquer sur l’onglet n°5 en haut, à partir de la gauche.

©2020 – Math’O karé SAS

Pour développer 3(2x-1), on utilise les flèches comme ci-dessous :

Pour développer -2(3x-2y), on utilise les flèches comme ci-dessous :

Pour développer \frac{1}{4}x(2x-1), on utilise les flèches comme ci-dessous :

Pour développer \sqrt{2}(\sqrt{5}x^2+\sqrt{3}), on utilise les flèches comme ci-dessous :

Pour développer 2xy(x^2+3y), on utilise les flèches comme ci-dessous :

Pour développer 3x^2y(2x^2+y^2+2x), on utilise les flèches comme ci-dessous :

J’écris a=3x donc a^{2}=(3x)^{2}={3^2}\times{x^2}=9x^2

J’écris b=5 donc b^{2}=25

Je calcule 2ab en remplaçant a et b par leurs valeurs 3x et 5 .

2ab=2\times 3x\times 5=30x

Je remplace a , b , a^{2}, 2ab et b^{2} par leurs valeurs dans

(a+b)^{2}=a^{2}+2ab+b^{2}

C’est-à-dire: (3x+5)^{2}=9x^{2}+30x+25

J’écris a=2x donc a^{2}=(2x)^{2}={2^2}\times{x^2}=4x^2

J’écris b=7 donc b^{2}=49

Je calcule 2ab en remplaçant a et b par leurs valeurs 2x et 7 .

2ab=2\times 2x\times 7=28x

Je remplace a , b , a^{2}, 2ab et b^{2} par leurs valeurs dans

(a+b)^{2}=a^{2}+2ab+b^{2}

C’est-à-dire: (2x+7)^{2}=4x^{2}+28x+49

J’écris a=6x donc a^{2}=(6x)^{2}={6^2}\times{x^2}=36x^2

J’écris b=\frac{2}{5} donc b^{2}=\frac{4}{25}

Je calcule 2ab en remplaçant a et b par leurs valeurs 6x et \frac{2}{5} .

2ab=2\times 6x\times {\frac{2}{5}}=\frac{24}{5}x

Je remplace a , b , a^{2}, 2ab et b^{2} par leurs valeurs dans

(a+b)^{2}=a^{2}+2ab+b^{2}

C’est-à-dire: (6x+\frac{2}{5})^{2}=36x^{2}+\frac{24}{5}x+\frac{4}{25}

J’écris a=x donc a^{2}=x^{2}

J’écris b=\sqrt{2} donc b^{2}=2

Je calcule 2ab en remplaçant a et b par leurs valeurs x et \sqrt{2} .

2ab=2\times x\times \sqrt{2}=2x\sqrt{2}

Je remplace a , b , a^{2}, 2ab et b^{2} par leurs valeurs dans

(a+b)^{2}=a^{2}+2ab+b^{2}

C’est-à-dire: (x+\sqrt{2})^{2}=x^{2}+2x\sqrt{2}+2

J’écris a=\frac{1}{2}x donc a^{2}=(\frac{1}{2}x)^{2}={(\frac{1}{2})^2}\times{x^2}=\frac{1}{4}x^2

J’écris b=\frac{1}{3} donc b^{2}=\frac{1}{9}

Je calcule 2ab en remplaçant a et b par leurs valeurs \frac{1}{2}x et \frac{1}{3} .

2ab=2\times \frac{1}{2}x\times {\frac{1}{3}}=\frac{1}{3}x

Je remplace a , b , a^{2}, 2ab et b^{2} par leurs valeurs dans

(a+b)^{2}=a^{2}+2ab+b^{2}

C’est-à-dire: (\frac{1}{2}x+\frac{1}{3})^{2}=\frac{1}{4}x^{2}+\frac{1}{3}x+\frac{1}{9}

J’écris a=2x donc a^{2}=(2x)^{2}={2^2}\times{x^2}=4x^2

J’écris b=7 donc b^{2}=49

Je calcule 2ab en remplaçant a et b par leurs valeurs 2x et 7 .

2ab=2\times 2x\times 7=28x

Je remplace a , b , a^{2}, 2ab et b^{2} par leurs valeurs dans

(a-b)^{2}=a^{2}-2ab+b^{2}

C’est-à-dire: (2x-7)^{2}=4x^{2}-28x+49

 

J’écris a=x donc a^{2}=x^2

J’écris b=\sqrt{3} donc b^{2}=3

Je calcule 2ab en remplaçant a et b par leurs valeurs x et \sqrt{3} .

2ab=2\times x\times \sqrt{3}=2\sqrt{3}x

Je remplace a , b , a^{2}, 2ab et b^{2} par leurs valeurs dans

(a-b)^{2}=a^{2}-2ab+b^{2}

C’est-à-dire: (x-\sqrt{3})^{2}=x^{2}-2\sqrt{3}x+3

J’écris a=\frac{1}{2}x donc a^{2}=\frac{1}{4}x^{2}

J’écris b=5 donc b^{2}=25

Je calcule 2ab en remplaçant a et b par leurs valeurs \frac{1}{2}x et 5 .

2ab=2\times \frac{1}{2}x\times 5=5x

Je remplace a , b , a^{2}, 2ab et b^{2} par leurs valeurs dans

(a-b)^{2}=a^{2}-2ab+b^{2}

C’est-à-dire: (\frac{1}{2}x-5)^{2}=\frac{1}{4}x^{2}-5x+25

 

J’écris a=4x donc a^{2}==(4x)^2={4^2}\times{x^2}=16x^2

J’écris b=\frac{1}{3} donc b^{2}=\frac{1}{9}

Je calcule 2ab en remplaçant a et b par leurs valeurs 4x et \frac{1}{3} .

2ab=2\times 4x\times \frac{1}{3}=\frac{8}{3}x

Je remplace a , b , a^{2}, 2ab et b^{2} par leurs valeurs dans

(a-b)^{2}=a^{2}-2ab+b^{2}

C’est-à-dire: (4x-\frac{1}{3})^{2}=16x^{2}-\frac{8}{3}x+\frac{1}{9}

 

J’écris a=\frac{1}{4}x donc a^{2}=\frac{1}{16}x^{2}

J’écris b=\frac{1}{2} donc b^{2}=\frac{1}{4}

Je calcule 2ab en remplaçant a et b par leurs valeurs \frac{1}{4}x et \frac{1}{2} .

2ab=2\times \frac{1}{4}x\times \frac{1}{2}=\frac{1}{4}x

Je remplace a , b , a^{2}, 2ab et b^{2} par leurs valeurs dans

(a-b)^{2}=a^{2}-2ab+b^{2}

C’est-à-dire: (\frac{1}{4}x-\frac{1}{2})^{2}=\frac{1}{16}x^{2}-\frac{1}{4}x+\frac{1}{4}

J’écris a=x donc a^{2}=x^{2}

J’écris b=5 donc b^{2}=25

Je remplace a , b , a^{2}, et b^{2} par leurs valeurs dans

(a-b)(a+b)=a^{2}-b^{2}

(x-5)(x+5)=x^{2}-25

J’écris a=2x donc a^{2}=(2x)^{2}=2^2\times x^2=4x^2

J’écris b=3 donc b^{2}=9

Je remplace a , b , a^{2}, et b^{2} par leurs valeurs dans

(a-b)(a+b)=a^{2}-b^{2}

(2x-3)(2x+3)=4x^{2}-9

J’écris a=x donc a^{2}=x^{2}

J’écris b=\sqrt{2} donc b^{2}=2

Je remplace a , b , a^{2}, et b^{2} par leurs valeurs dans

(a-b)(a+b)=a^{2}-b^{2}

(x-\sqrt{2})(x+\sqrt{2})=x^{2}-2

J’écris a=\frac{1}{5}x donc a^{2}=\frac{1}{25}x^{2}

J’écris b=4 donc b^{2}=16

Je remplace a , b , a^{2}, et b^{2} par leurs valeurs dans

(a-b)(a+b)=a^{2}-b^{2}

(\frac{1}{5}x-4)(\frac{1}{5}x+4)=\frac{1}{25}x^{2}-16

J’écris a=\frac{1}{7}x donc a^{2}=\frac{1}{49}x^{2}

J’écris b=\frac{1}{5} donc b^{2}=\frac{1}{25}

Je remplace a , b , a^{2}, et b^{2} par leurs valeurs dans

(a-b)(a+b)=a^{2}-b^{2}

(\frac{1}{7}x-\frac{1}{5})(\frac{1}{7}x+\frac{1}{5})=\frac{1}{49}x^{2}-\frac{1}{25}

On va développer 2(x-7)^{2}.

La priorité des opérations impose d’effectuer d’abord la puissance ( ici 2 )

J’écris a=x donc a^{2}=x^{2}

J’écris b=7 donc b^{2}=49

Je calcule 2ab en remplaçant a et b par leurs valeurs x et 7 .

2ab=2\times x\times 8=14x

Je remplace a , b , a^{2}, 2ab et b^{2} par leurs valeurs dans

(a-b)^{2}=a^{2}-2ab+b^{2}

C’est-à-dire: (x-7)^{2}=x^{2}-14x+49

Après les puissances, on effectue la multiplication en utilisant les flèches comme ci-dessous :

Voici comment rédiger la réponse :

2(x-7)^{2}=2(x^{2}-14x+49)\\\hspace{1.5 cm}=2x^{2}-28x+98

 

On va développer 2x(3x-1)^{2}.

La priorité des opérations impose d’effectuer d’abord la puissance ( ici 2 )

J’écris a=3x donc a^{2}=(3x)^{2}=3^{2}x^{2}=9x^{2}

J’écris b=1 donc b^{2}=1

Je calcule 2ab en remplaçant a et b par leurs valeurs 3x et 1 .

2ab=2\times 3x\times 1=6x

Je remplace a , b , a^{2}, 2ab et b^{2} par leurs valeurs dans

(a-b)^{2}=a^{2}-2ab+b^{2}

C’est-à-dire: (3x-1)^{2}=9x^{2}-6x+1

Après les puissances, on effectue la multiplication en utilisant les flèches comme ci-dessous :

Voici comment rédiger la réponse :

2x(3x-1)^{2}=2x(9x^{2}-6x+1)\\\hspace{1.9 cm}=18x^{3}-12x^{2}+2x

 

On va développer x(x+5)^{2}+3x.

La priorité des opérations impose d’effectuer d’abord la puissance ( ici 2 )

J’écris a=x donc a^{2}=x^{2}

J’écris b=5 donc b^{2}=25

Je calcule 2ab en remplaçant a et b par leurs valeurs x et 5 .

2ab=2\times x\times 5=10x

Je remplace a , b , a^{2}, 2ab et b^{2} par leurs valeurs dans

(a+b)^{2}=a^{2}+2ab+b^{2}

C’est-à-dire: (x+5)^{2}=x^{2}+10x+25

Après les puissances, on effectue la multiplication en utilisant les flèches comme ci-dessous :

Après la puissance et  la multiplication on effectue l’addition ( il faut ajouter 3x )

Voici comment rédiger la réponse :

x(x+5)^{2}+3x=x(x^{2}+10x+25)+3x\\\hspace{2.1 cm}=x^{3}+10x^{2}+25x+3x\\\hspace{2.1 cm}=x^{3}+10x^{2}+28x

 

On va développer 3(2x-1)^{2}+1.

La priorité des opérations impose d’effectuer d’abord la puissance ( ici 2 )

J’écris a=2x donc a^{2}=(2x)^{2}=2^2\times{x^2}=4x^2

J’écris b=1 donc b^{2}=1

Je calcule 2ab en remplaçant a et b par leurs valeurs 2x et 1 .

2ab=2\times 2x\times 1=4x

Je remplace a , b , a^{2}, 2ab et b^{2} par leurs valeurs dans

(a-b)^{2}=a^{2}-2ab+b^{2}

C’est-à-dire: (2x-1)^{2}=4x^{2}-4x+1

Après les puissances, on effectue la multiplication en utilisant les flèches comme ci-dessous :

Après la puissance et  la multiplication on effectue l’addition ( il faut ajouter 1 )

Voici comment rédiger la réponse :

3(2x-1)^{2}+1=3(4x^{2}-4x+1)+1\\\hspace{2.1 cm}=12x^{2}-12x+3+1\\\hspace{2.1 cm}=12x^{2}-12x+4

 

 

On va développer 4(3x+1)^{2}-10.

La priorité des opérations impose d’effectuer d’abord la puissance ( ici 2 )

J’écris a=3x donc a^{2}=(3x)^{2}=3^2\times{x^2}=9x^2

J’écris b=1 donc b^{2}=1

Je calcule 2ab en remplaçant a et b par leurs valeurs 3x et 1 .

2ab=2\times 3x\times 1=6x

Je remplace a , b , a^{2}, 2ab et b^{2} par leurs valeurs dans

(a+b)^{2}=a^{2}+2ab+b^{2}

C’est-à-dire: (3x+1)^{2}=9x^{2}+6x+1

Après les puissances, on effectue la multiplication en utilisant les flèches comme ci-dessous :

Après la puissance et  la multiplication on effectue l’addition ( il faut enlever 10 )

Voici comment rédiger la réponse :

4(3x+1)^{2}-10=4(9x^{2}+6x+1)+1\\\hspace{2.1 cm}=36x^{2}+24x+4-10\\\hspace{2.1 cm}=36x^{2}+24x-6

 

 

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.