Sommaire
Exercice n°1
Soit ABC un triangle rectangle en A.
On a BA=3 et AC=5.
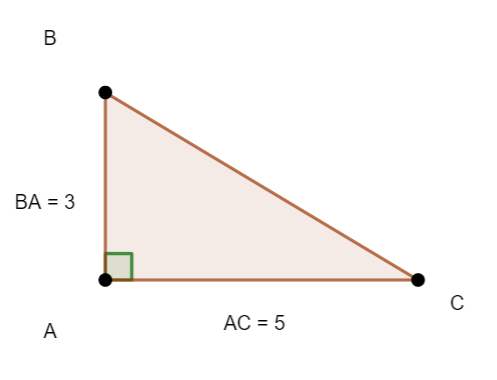
On veut calculer la mesure en degrés de l’angle aigu \widehat{C}.
- Dans le triangle rectangle ABC, que représente le côté [AC] pour l’angle \widehat{C}.
2. Dans le triangle rectangle ABC, que représente le côté [AB] pour l’angle \widehat{C}.
3. Ecrire les trois relations trigonométriques dans le triangle rectangle ABC pour l’angle \widehat{C}. Puis choisir celle qui nous permettra de trouver la mesure en degrés de l’angle \widehat{C} et la déterminer.
Exercice n°2
Soit ABC un triangle rectangle en A.
On a AB=5 et BC=7.78.
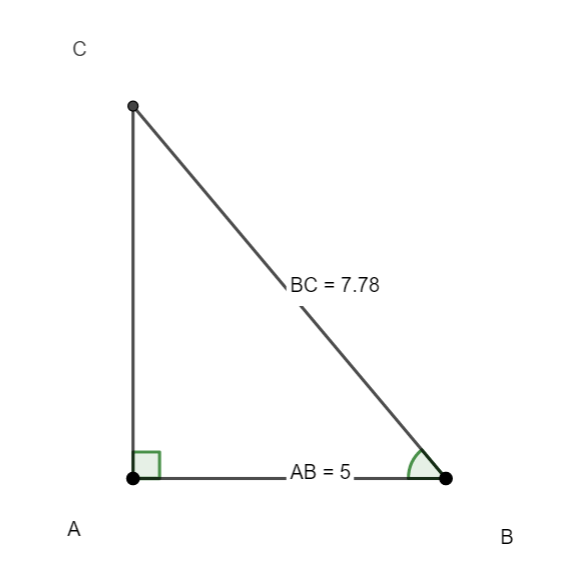
On veut calculer la mesure en degrés de l’angle aigu \widehat{B}.
- Dans le triangle rectangle ABC, que représente le côté [AB] pour l’angle \widehat{B}.
2. Dans le triangle rectangle ABC, que représente le côté [BC] pour l’angle \widehat{B}.
3. Ecrire les trois relations trigonométriques dans le triangle rectangle ABC pour l’angle \widehat{B}. Puis choisir celle qui nous permettra de trouver la mesure en degrés de l’angle \widehat{B} et la déterminer.
Exercice n°3
Soit ABC un triangle rectangle en B.
On a AC=6.39 et CB=2.18.
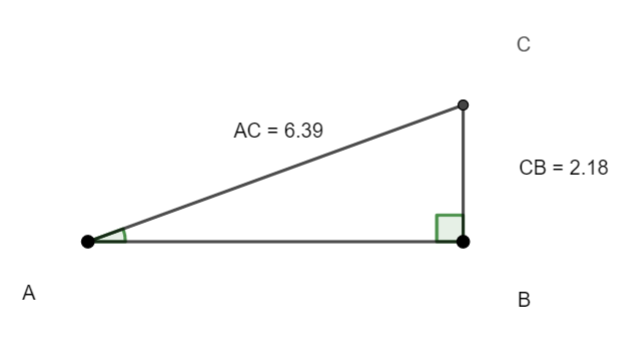
On veut calculer la mesure en degrés de l’angle aigu \widehat{A}.
- Dans le triangle rectangle ABC, que représente le côté [AC] pour l’angle \widehat{A}.
2. Dans le triangle rectangle ABC, que représente le côté [BC] pour l’angle \widehat{A}.
3. Ecrire les trois relations trigonométriques dans le triangle rectangle ABC pour l’angle \widehat{A}. Puis choisir celle qui nous permettra de trouver la mesure en degrés de l’angle \widehat{A} et la déterminer.
Exercice n°4
Soit ABC un triangle rectangle en B.
On a AC=9.12 et \widehat{A}=64°.
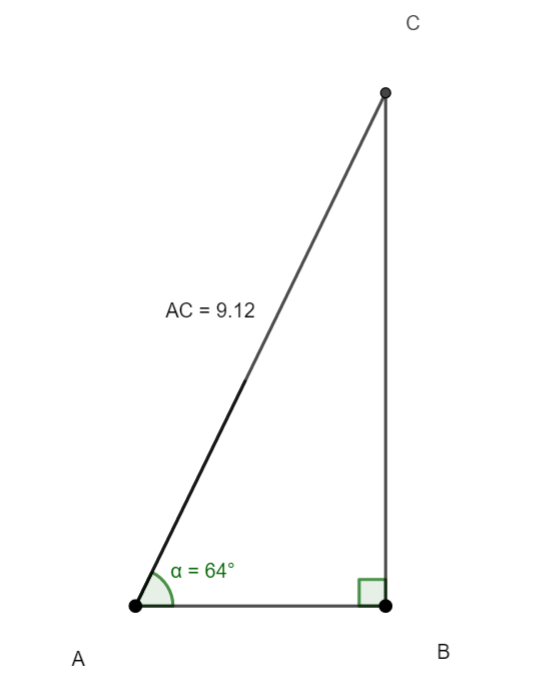
On veut calculer la distance AB.
- Dans le triangle rectangle ABC, que représente le côté [AC] pour l’angle \widehat{A}.
2. Dans le triangle rectangle ABC, que représente le côté [AB] pour l’angle \widehat{A}.
3. Ecrire les trois relations trigonométriques dans le triangle rectangle ABC pour l’angle \widehat{A}. Puis choisir celle qui nous permettra de trouver la distance AB et la déterminer.
Exercice n°5
Soit ABC un triangle rectangle en A.
On a BA=4.09 et \widehat{B}=35°.
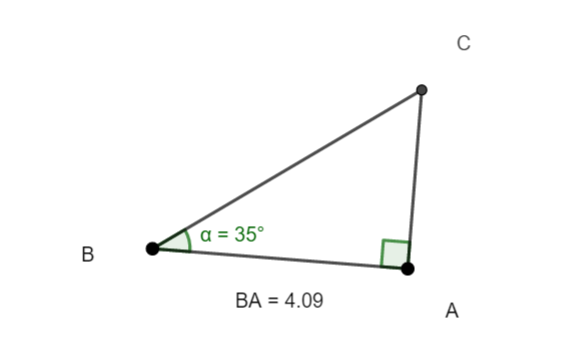
On veut calculer la distance BC.
- Dans le triangle rectangle ABC, que représente le côté [BA] pour l’angle \widehat{B}.
2. Dans le triangle rectangle ABC, que représente le côté [BC] pour l’angle \widehat{B}.
3. Ecrire les trois relations trigonométriques dans le triangle rectangle ABC pour l’angle \widehat{B}. Puis choisir celle qui nous permettra de trouver la distance BC et la déterminer.
Exercice n°6
Soit ABC un triangle rectangle en B.
On a BA=6 et \widehat{A}=45°.
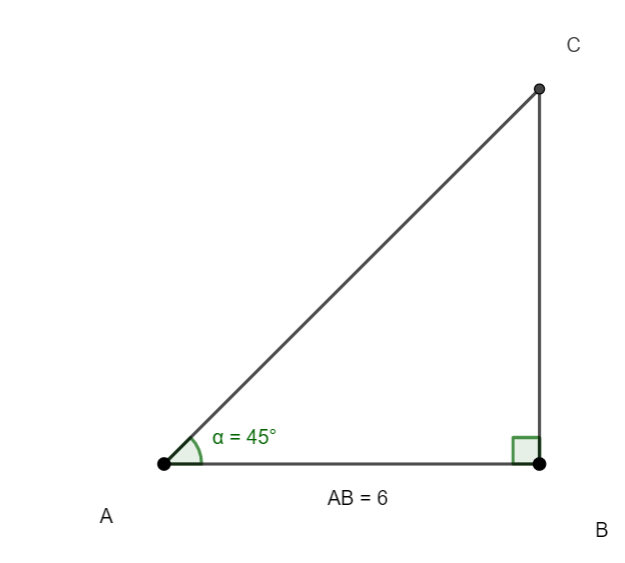
On veut calculer la distance BC.
- Dans le triangle rectangle ABC, que représente le côté [BA] pour l’angle \widehat{A}.
2. Dans le triangle rectangle ABC, que représente le côté [BC] pour l’angle \widehat{A}.
3. Ecrire les trois relations trigonométriques dans le triangle rectangle ABC pour l’angle \widehat{A}. Puis choisir celle qui nous permettra de trouver la distance BC et la déterminer.
Exercice n°7
On considère un angle aigu de mesure \alpha tel que cos\alpha=\frac{\sqrt3}{2}. Calculer sin\alpha.
Exercice n°8
On considère un angle aigu de mesure \alpha tel que sin\alpha=0.6. Calculer cos\alpha.



