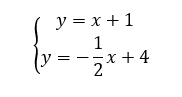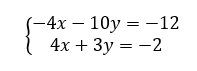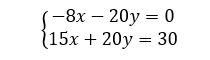logo

2. systèmes d’équations. Exercices.

Sommaire

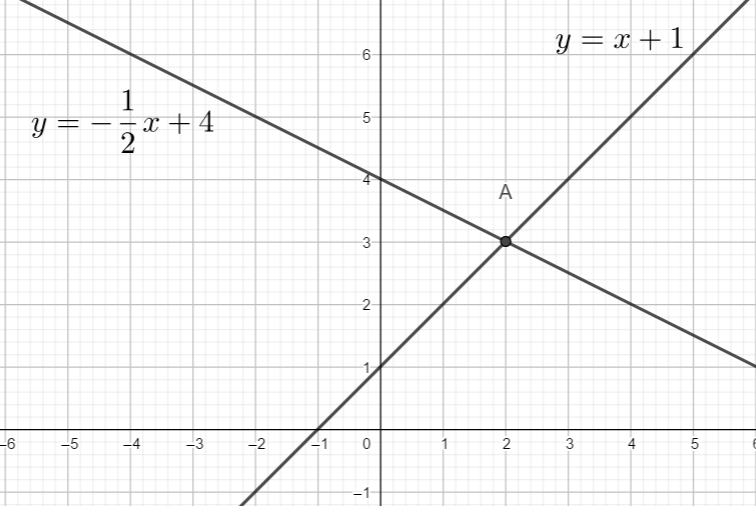
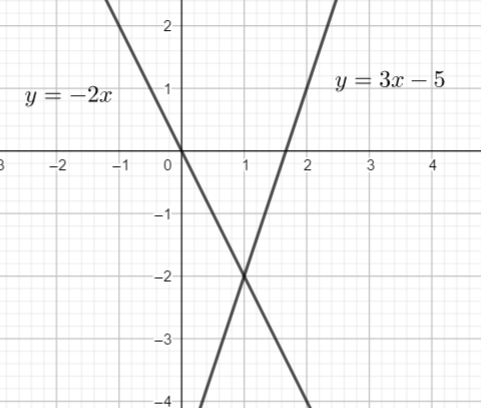
Exercice n°1 

Résoudre graphiquement le système suivant :

correction

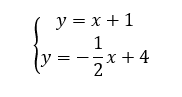
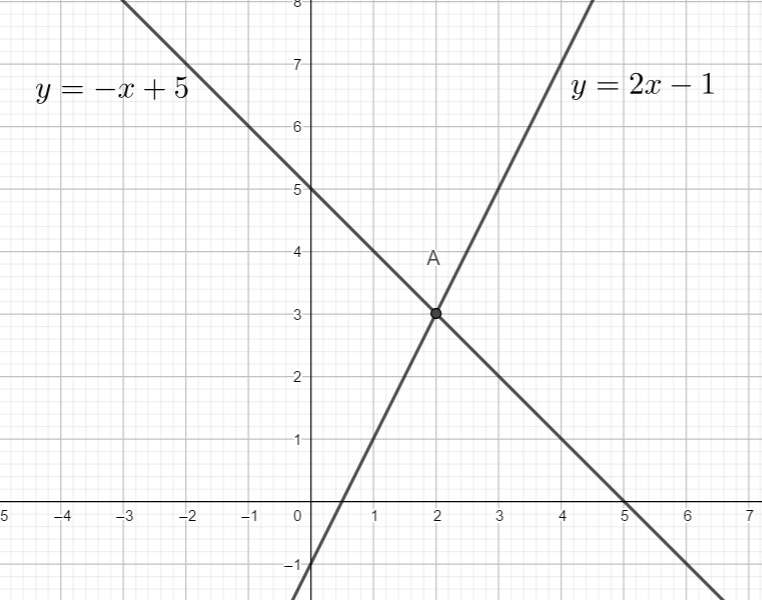
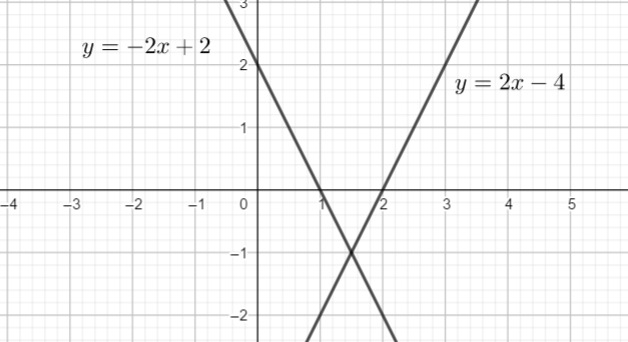
Exercice n°2

Résoudre graphiquement le système suivant :

correction

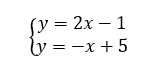
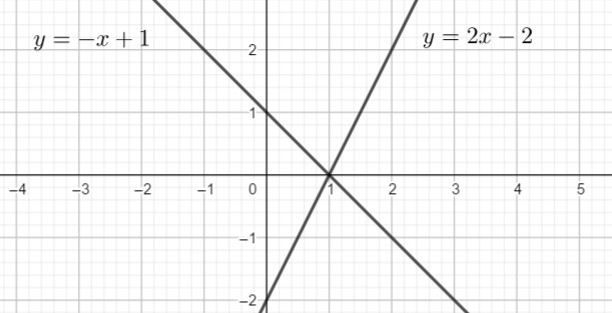
Exercice n°3

résoudre les systèmes suivants graphiquement.

correction
correction
correction

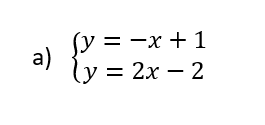
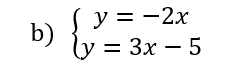
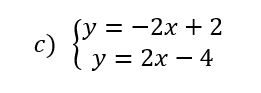
Pour valider les réponses des exos 1, 2 et 3 avec une page graphique de Géogébra.

Valider vos calculs avec la fenêtre Géogébra ci-dessous :

Exercice n°4 

Résoudre, par le calcul et par substitution, le système de deux équations à deux inconnues suivant :

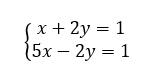
conjecturer le résultat avec la TI 83
correction

Exercice n°5

Résoudre, par le calcul et par substitution, le système de deux équations à deux inconnues suivant :

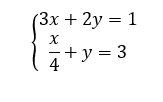
conjecturer le résultat avec la TI 83
correction

Exercice n°6 

Résoudre, par le calcul et par combinaison linéaire, le système de deux équations à deux inconnues suivant :

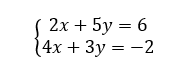
conjecturer le résultat avec la TI 83
correction

Exercice n°7

Résoudre, par le calcul et par combinaison linéaire, le système de deux équations à deux inconnues suivant :

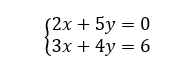
conjecturer le résultat avec la TI 83
correction

Pour valider les réponses des exos 4, 5, 6 et 7 avec une page de calcul formel de Géogébra.

Valider vos calculs avec la fenêtre Géogébra ci-dessous :

©2020 – Math’O karé SAS

On veut résoudre graphiquement le système :

On trace les deux droites dans le repère avec la méthode de son choix. Par exemple en utilisant ordonnée à l’origine et coefficient directeur.

    Dans y=x+1 on identifie le coefficient directeur a=1 et l’ordonnée à l’origine b=1 . On place 1 sur l’axe des ordonnées. A partir du point de coordonnées (0;1), j’avance horizontalement de 1 vers la droite et je monte  de 1 (a=1 ). J’obtiens alors le deuxième point. Je trace ensuite la droite qui passe par les deux points.

    Dans y=-\frac{1}{2}x+4 on identifie le coefficient directeur a=-\frac{1}{2} et l’ordonnée à l’origine b=4 . On place4  sur l’axe des ordonnées. A partir du point de coordonnées (0;4), j’avance horizontalement de 1 vers la droite et je descends de \frac{1}{2} (a=-\frac{1}{2} ). J’obtiens alors le deuxième point. Je trace ensuite la droite qui passe par les deux points.

Le couple solution est (2;3).

 

On veut résoudre graphiquement le système :

On trace les deux droites dans le repère avec la méthode de son choix. Par exemple en utilisant ordonnée à l’origine et coefficient directeur.

    Dans y=2x-1 on identifie le coefficient directeur a=2 et l’ordonnée à l’origine b=-1 . On place -1 sur l’axe des ordonnées. A partir du point de coordonnées (0;-1), j’avance horizontalement de 1 vers la droite et je monte  de 2 (a=2 ). J’obtiens alors le deuxième point. Je trace ensuite la droite qui passe par les deux points.

    Dans y=-x+5 on identifie le coefficient directeur a=-1 et l’ordonnée à l’origine b=5 . On place5  sur l’axe des ordonnées. A partir du point de coordonnées (0;5), j’avance horizontalement de 1 vers la droite et je descends de 1 (a=-1 ). J’obtiens alors le deuxième point. Je trace ensuite la droite qui passe par les deux points.

Le couple solution est (2;3).

 

On veut résoudre graphiquement le système :

On trace les deux droites dans le repère avec la méthode de son choix. Par exemple en utilisant ordonnée à l’origine et coefficient directeur.

    Dans y=-x+1 on identifie le coefficient directeur a=-1 et l’ordonnée à l’origine b=1 . On place 1 sur l’axe des ordonnées. A partir du point de coordonnées (0;1), j’avance horizontalement de 1 vers la droite et je descends de 1 (a=-1 ). J’obtiens alors le deuxième point. Je trace ensuite la droite qui passe par les deux points.

    Dans y=2x-2 on identifie le coefficient directeur a=2 et l’ordonnée à l’origine b=-2 . On place-2  sur l’axe des ordonnées. A partir du point de coordonnées (0;-2), j’avance horizontalement de 1 vers la droite et je monte de 2 (a=2 ). J’obtiens alors le deuxième point. Je trace ensuite la droite qui passe par les deux points.

Le couple solution est (1;0).

On veut résoudre graphiquement le système :

On trace les deux droites dans le repère avec la méthode de son choix. Par exemple en utilisant ordonnée à l’origine et coefficient directeur.

    Dans y=-2x on identifie le coefficient directeur a=-2 et l’ordonnée à l’origine b=0 . On place 0 sur l’axe des ordonnées. A partir du point de coordonnées (0;0), j’avance horizontalement de 1 vers la droite et je descends de 2 (a=-2 ). J’obtiens alors le deuxième point. Je trace ensuite la droite qui passe par les deux points.

    Dans y=3x-5 on identifie le coefficient directeur a=3 et l’ordonnée à l’origine b=-5 . On place-5  sur l’axe des ordonnées. A partir du point de coordonnées (0;-5), j’avance horizontalement de 1 vers la droite et je monte de 3 (a=3 ). J’obtiens alors le deuxième point. Je trace ensuite la droite qui passe par les deux points.

Le couple solution est (1;-2).

On veut résoudre graphiquement le système :

On trace les deux droites dans le repère avec la méthode de son choix. Par exemple en utilisant ordonnée à l’origine et coefficient directeur.

    Dans y=-2x+2 on identifie le coefficient directeur a=-2 et l’ordonnée à l’origine b=2 . On place 2 sur l’axe des ordonnées. A partir du point de coordonnées (0;2), j’avance horizontalement de 1 vers la droite et je descends de 2 (a=-2 ). J’obtiens alors le deuxième point. Je trace ensuite la droite qui passe par les deux points.

    Dans y=2x-4 on identifie le coefficient directeur a=2 et l’ordonnée à l’origine b=-4 . On place-4  sur l’axe des ordonnées. A partir du point de coordonnées (0;-4), j’avance horizontalement de 1 vers la droite et je monte de 2 (a=2 ). J’obtiens alors le deuxième point. Je trace ensuite la droite qui passe par les deux points.

Le couple solution est (\frac{3}{2};-1).

On veut résoudre par le calcul et par substitution le système suivant :

L’objectif est d’éliminer une des deux inconnues pour obtenir une équation à une seule inconnue. Je choisis d’éliminer x.

A l’aide de la 1ère équation, j’exprime x en fonction de y.

2y n’est pas à sa place, j’enlève 2y de chaque côté.

x=-2y+1

Je remplace x par (-2y+1) entre parenthèses dans la deuxième équation pour obtenir une équation du premier degré à une seule inconnue :

5(-2y+1)-2y=1

Je développe 5(-2y+1)

-10y+5-2y=1

Je réduis le membre de gauche

-12y+5=1

5 n’est pas à sa place, j’enlève 5 de chaque côté.

-12y=1-5\\-12y=-4

-12 n’est pas à sa place dans le membre de gauche, c’est un facteur dans un produit. Je divise par  -12 de chaque côté.

y=\frac{-4}{-12}

On simplifie \frac{-4}{-12}par -4

y=\frac{1}{3}

Pour déterminer x , je remplace y par \frac{1}{3} dans, par exemple, la première équation.

x+{2}\times{\frac{1}{3}}=1

x+\frac{2}{3}=1

\frac{2}{3} n’est pas à sa place dans le membre de gauche, j’enlève \frac{2}{3} de chaque côté.

x=1-\frac{2}{3}

On met au même dénominateur, ici 3.

x={1}\times{\frac{3}{3}}-\frac{2}{3}

x=\frac{3}{3}-\frac{2}{3}

x=\frac{1}{3}

Le couple solution est (\frac{1}{3};\frac{1}{3})

 

On veut résoudre par le calcul et par substitution le système suivant :

L’objectif est d’éliminer une des deux inconnues pour obtenir une équation à une seule inconnue. Je choisis d’éliminer y.

A l’aide de la 2nde équation, j’exprime y en fonction de x.

\frac{x}{4} n’est pas à sa place, j’enlève \frac{x}{4} de chaque côté.

y=-\frac{x}{4}+3

Je remplace y par (-\frac{x}{4}+3) entre parenthèses dans la première équation pour obtenir une équation du premier degré à une seule inconnue :

3x+2(-\frac{x}{4}+3)=1

Je développe 2(-\frac{x}{4}+3)

3x-{2}\times{\frac{x}{4}}+2\times3=1

Je réduis le membre de gauche

3x-\frac{x}{2}+6=1\\{3x}\times{\frac{2}{2}}-\frac{x}{2}+6=1\\\frac{6x}{2}-\frac{x}{2}+6=1\\\frac{5x}{2}+6=1

6 n’est pas à sa place, j’enlève 6 de chaque côté.

\frac{5x}{2}=1-6\\\frac{5x}{2}=-5

\frac{5}{2} n’est pas à sa place dans le membre de gauche, c’est un facteur dans un produit. Je divise par  \frac{5}{2}de chaque côté, ce qui revient à multiplier par l’inverse\frac{2}{5}.

x={-5}\times{\frac{2}{5}}

On simplifie par 5.

x=-2

Pour déterminer y , je remplace x par -2 dans, par exemple, la première équation.

{3}\times{(-2)}+2y=1

-6+2y=1

-6 n’est pas à sa place dans le membre de gauche, j’ajoute 6 de chaque côté.

2y=1+6

2y=7

Le 2 à gauche n’est pas à sa place, je divise par 2 de chaque côté.

y=\frac{7}{2}

Le couple solution est (-2;\frac{7}{2})

 

Il s’agit de résoudre par le calcul et par combinaison linéaire, le système suivant :

Je décide d’éliminer les x , pour cela je dois multiplier la première équation par -2.

Ainsi on aura -4x dans la nouvelle première équation et son opposé 4x  dans la deuxième équation.

ATTENTION : quand on dit que je dois multiplier la première équation par -2 , je multiplie tout par -2                         

J’ajoute membre à membre ces deux égalités (les x disparaissent, ce qui était le but recherché)

-10y+3y=-12-2\\-7y=-14

-7 n’est pas à sa place dans le membre de gauche, c’est un facteur dans un produit. On divise par-7 de chaque côté.

y=\frac{-14}{-7}\\y=2

Pour déterminer la valeur de x  je remplace y par 2  dans par exemple la première équation de départ.

2x+{5}\times{2}=6\\2x+10=6

10 n’est pas à sa place dans le membre de gauche, c’est un terme dans une somme. On enlève   10 de chaque côté.

2x=6-10\\2x=-4

2 n’est pas à sa place dans le membre de gauche, c’est un facteur dans un produit. On divise par2 de chaque côté.

x=\frac{-4}{2}\\x=-2

Le couple solution est (-2;2)

 

Il s’agit de résoudre par le calcul et par combinaison linéaire, le système suivant :

Je décide d’éliminer les y , pour cela je dois multiplier la première équation par -4 et la deuxième équation par 5.

Ainsi on aura -20y dans la nouvelle première équation et son opposé 20y  dans la nouvelle deuxième équation.

ATTENTION : quand on dit que je dois multiplier la première équation par -4 , je multiplie tout par -4

                         quand on dit que je dois multiplier la deuxième  équation par  5 , je multiplie tout par 5   .

J’ajoute membre à membre ces deux égalités (les y disparaissent, ce qui était le but recherché)

-8x+15x=0+30\\7x=30

7 n’est pas à sa place dans le membre de gauche, c’est un facteur dans un produit. On divise par 7 de chaque côté.

x=\frac{30}{7}

Pour déterminer la valeur de y  je remplace x par \frac{30}{7}  dans par exemple la première équation.

{2}\times{\frac{30}{7}}+5y=0

\frac{60}{7}+5y=0

\frac{60}{7} n’est pas à sa place dans le membre de gauche, c’est un terme dans une somme. On enlève  \frac{60}{7} de chaque côté.

5y=-\frac{60}{7}

5 n’est pas à sa place dans le membre de gauche, c’est un facteur dans un produit. On divise par  5 de chaque côté.

y=\frac{-\frac{60}{7}}{5}

y={-\frac{60}{7}}\times{\frac{1}{5}}

Avant de multiplier numérateurs et dénominateurs, simplifions en haut et en bas par 5.

y=-\frac{12}{7}

Le couple solution est (\frac{30}{7};-\frac{12}{7})

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.