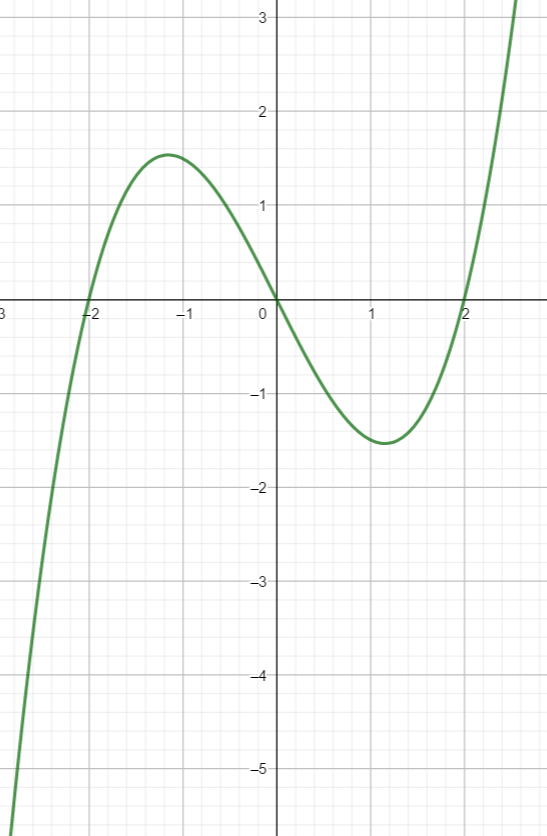
résoudre graphiquement les inéquations suivantes à l’aide de la courbe ci-dessous.
f(x)>2 et f(x)\leq 0.
Résoudre graphiquement f(x)>2
Je résous :
f(x) > 2Je traduis en langue française :
la courbe est située au-dessus et pas sur la droite D : y=2
Je place mon index sur l’extrémité gauche de la courbe et je parcours la courbe de la gauche vers la droite en disant oui quand la courbe est située au-dessus et pas sur la droite D d’équation y=2 et en disant non dans le cas contraire.
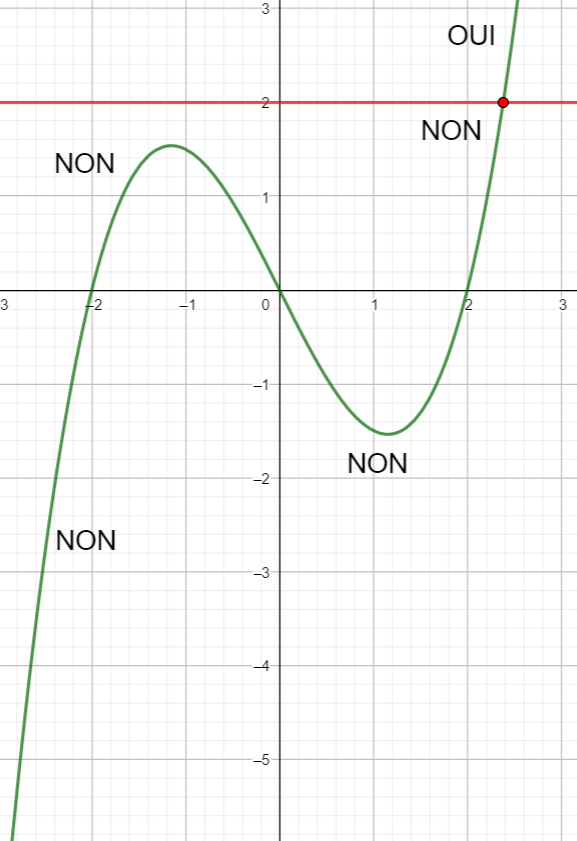
J’identifie sur l’axe des abscisses les valeurs de x pour lesquelles j’ai dit oui et j’écris cet ensemble sous forme d’intervalles ou de réunion d’intervalles
S=]2.4;2.6]Remarque : On a dit non pour la valeur 2.4 , on doit donc l’enlever de l’intervalle. Pour cela le crochet doit être ouvert c’est-à-dire tourné vers l’extérieur de l’intervalle.
On a dit oui pour la valeur 2.6 , on doit donc l’inclure dans l’intervalle. Pour cela le crochet doit être fermé c’est-à-dire tourné vers l’intérieur de l’intervalle.
Résoudre graphiquement f(x)\leq 0
Je résous :
f(x) \leq 0Je traduis en langue française :
la courbe est située en-dessous ou sur la droite D : y=0
Je place mon index sur l’extrémité gauche de la courbe et je parcours la courbe de la gauche vers la droite en disant oui quand la courbe est située en-dessous ou sur la droite D d’équation y=0 (c’est l’axe des abscisses) et en disant non dans le cas contraire.
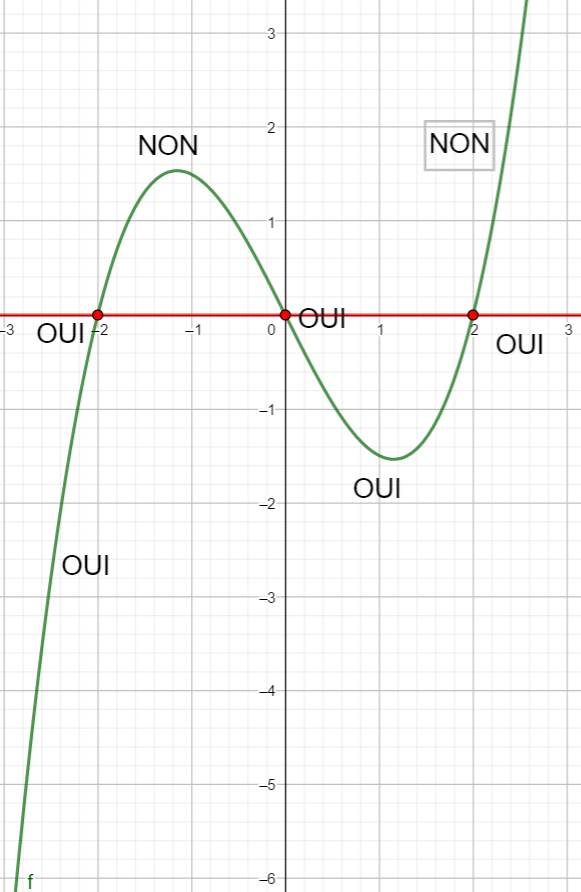
J’identifie sur l’axe des abscisses les valeurs de x pour lesquelles j’ai dit oui et j’écris cet ensemble sous forme d’intervalles ou de réunion d’intervalles
S=\left[-2.8;-2\right]\cup\left[0;2\right]Remarque : On a dit oui pour la valeur -2.8 , on doit donc l’inclure dans l’intervalle. Pour cela le crochet doit être fermé c’est-à-dire tourné vers l’intérieur de l’intervalle.
On a dit oui pour la valeur -2 , on doit donc l’inclure dans l’intervalle. Pour cela le crochet doit être fermé c’est-à-dire tourné vers l’intérieur de l’intervalle.
On a dit oui pour la valeur 0 , on doit donc l’inclure dans l’intervalle. Pour cela le crochet doit être fermé c’est-à-dire tourné vers l’intérieur de l’intervalle.
On a dit oui pour la valeur 2 , on doit donc l’inclure dans l’intervalle. Pour cela le crochet doit être fermé c’est-à-dire tourné vers l’intérieur de l’intervalle.



