Théorème :
Soit les réels a,b,c avec a\ne o, pour étudier le signe de ax²+bx+c,
on calcule \Delta=b²-4ac
si \Delta<0 , ax²+bx+c est toujours du signe de a.

si \Delta=0, ax²+bx+c est toujours du signe de a et s’annule pour x_0=-\frac{b}{2a} .

si \Delta>0 , l’équation admet deux solutions réelles notées
x_1=\frac{-b-\sqrt{\Delta}}{2a} et x_2=\frac{-b+\sqrt{\Delta}}{2a}.
ax²+bx+c est du signe de a à l’extérieur des racines et du signe de (-a) à l’intérieur des racines.
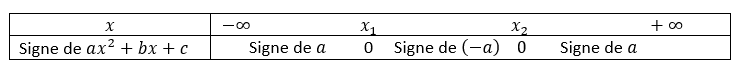
Remarque : pour le tableau ci-dessus, c’est x_1 qui est plus petit que x_2 mais ce n’est pas toujours le cas.
Exemple n°1 : Etudier le signe du polynôme -x^2+2x-1
1.Conjecture graphique : déterminons graphiquement le signe de la fonction f définie par
f(x)=-x^2+2x-1 graphiquement.
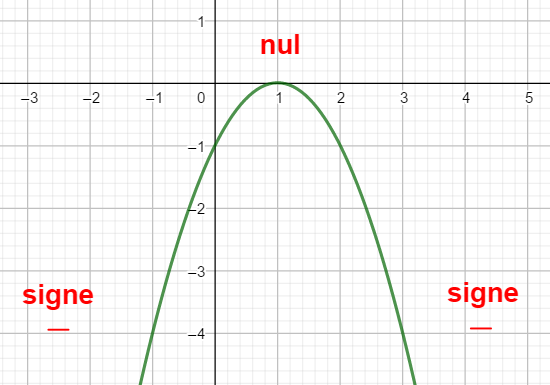
On conjecture donc graphiquement que le polynôme -x^2+2x-1 est de signe moins et s’annule pour x=1.
2. Etude du signe de -x^2+2x-1 par le calcul en utilisant le théorème plus haut.
J’identifie les coefficients l’équation a=-1, b=2 et c=-1.
Je calcule \Delta=b²-4ac en remplaçant a,b,c par (-1), 2, (-1) .
\Delta=2²-4\times{(-1)}\times{(-1)}\\\Delta=4-4\\\Delta=0comme \Delta=0, ax²+bx+c est toujours du signe de a et s’annule pour x_0=-\frac{b}{2a}
Je calcule x_0=-\frac{b}{2a} en remplaçant a,b par (-1), 2.
x_0=-\frac{2}{2\times{(-1)}}\\x_0=-\frac{2}{(-2)}\\x_0=1Je dresse le tableau de signes du polynôme:
Comme a=-1 le signe de a est négatif.

3. Vérification à l’aide de l’application Calcul Formel de Géogébra.
On peut par exemple chercher pour quelles valeurs de x le polynôme est de signe + puis compléter avec les –.
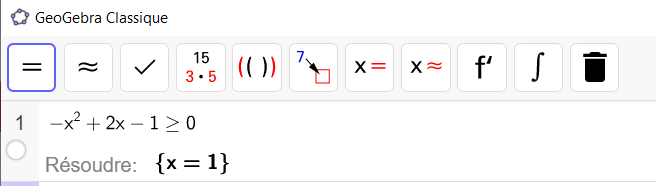
Il n’y a qu’une solution, celle pour laquelle le polynôme s’annule. Pour toutes les autres valeurs le polynôme est négatif.
Exemple n°2 : Etudier le signe du polynôme x^2-3x+1.
1.Conjecture graphique : déterminons graphiquement le signe de la fonction f définie par f(x)=x^2-3x+1 graphiquement.
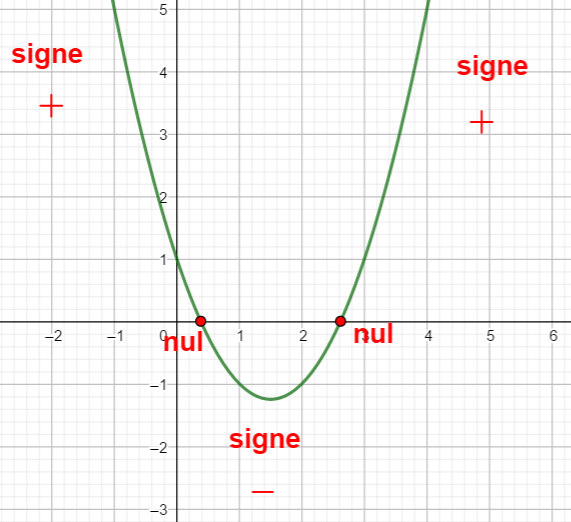
On conjecture donc graphiquement que le polynôme x^2-3x+1=0 est d’abord de signe + jusqu’à 0.4 puis de signe – jusqu’à 2.6 et ensuite de signe +.
2. Etude du signe de x^2-3x+1 par le calcul en utilisant le théorème plus haut.
J’identifie les coefficients l’équation a=1, b=-3 et c=1.
Je calcule \Delta=b²-4ac en remplaçant a,b,c par 1, (-3) ,1 .
\Delta=(-3)²-4\times{1}\times{1}\\\Delta=9-4\\\Delta=5Comme \Delta>0 , l’équation admet deux solutions réelles notées
x_1=\frac{-b-\sqrt{\Delta}}{2a} et x_2=\frac{-b+\sqrt{\Delta}}{2a}.
ax²+bx+c est du signe de a à l’extérieur des racines et du signe de (-a) à l’intérieur des racines.
Je calcule x_1=\frac{-b-\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta par 1, (-3), 5.
x_1=\frac{-(-3)-\sqrt{5}}{2\times{1}}\\x_1=\frac{3-\sqrt{5}}{2}Je calcule x_2=\frac{-b+\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta par 1, (-3) , 5.
x_2=\frac{-(-3)+\sqrt{5}}{2\times{1}}\\x_2=\frac{3+\sqrt{5}}{2}Je dresse le tableau de signes du polynôme:
Comme a=1 le signe de a est positif.

3. Vérification à l’aide de l’application Calcul Formel de Géogébra.
On peut par exemple chercher pour quelles valeurs de x le polynôme est de signe + puis compléter avec les –.

Exemple n°3 : Etudier le signe du polynôme 2x^2-4x+3.
1.Conjecture graphique : déterminons graphiquement le signe de la fonction f définie par
f(x)=2x^2-4x+3 graphiquement.
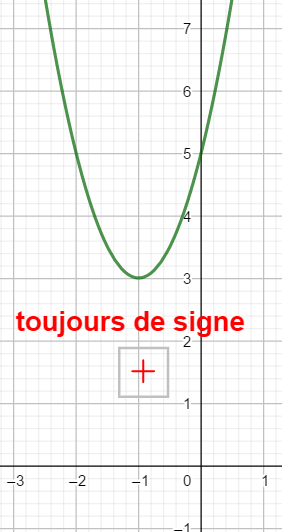
On conjecture donc graphiquement que le polynôme 2x^2+4x+3=0 est toujours de signe + et ne s’annule jamais .
2. Etude du signe de 2x^2+4x+3 par le calcul en utilisant le théorème plus haut.
J’identifie les coefficients l’équation a=2, b=4 et c=3.
Je calcule \Delta=b²-4ac en remplaçant a,b,c par 2,4,3 .
\Delta=4²-4\times{2}\times{3}\\\Delta=16-24\\\Delta=-8comme \Delta<0 , ax²+bx+c est toujours du signe de a.
Comme a=2, 2x²+4x+3 est toujours du signe de signe +.

3. Vérification à l’aide de l’application Calcul Formel de Géogébra.
On peut par exemple chercher pour quelles valeurs de x le polynôme est de signe + puis compléter avec les –.

La réponse signifie que cette inégalité est toujours vraie donc que le polynôme est toujours positif.



