SOMMAIRE
Les fonctions de référence:
Fonction carré.
Représentation graphique
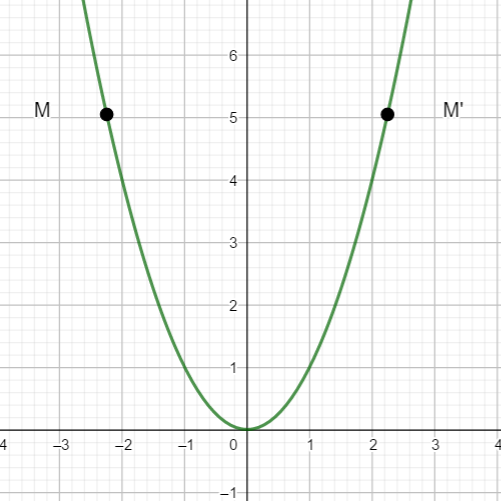
Pour un point M quelconque situé sur la courbe, son symétrique, par rapport à l’axe des ordonnées, M’ est lui aussi situé sur la courbe. On dit que l’axe des ordonnées est axe de symétrie de la courbe de la fonction carré.,
Représentation tableur
Voici le tableur de la calculatrice TI-83 pour la fonction carré.

On constate dans ce tableau de valeurs que 5 et -5 ont la même image 25, qu’il en va de même pour 4 et -4 qui ont pour image commune 16……
Représentation algébrique
La fonction carré est définie sur \mathbf{R}.
Si x \in\mathbf{R} alors -x \in\mathbf{R} et (-x)^2=x^2 .
On dit que la fonction carré est paire.
Fonction cube.
Représentation graphique
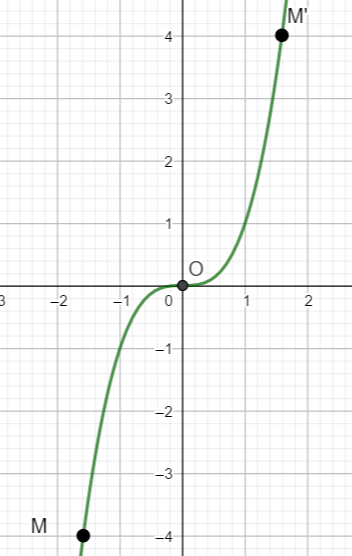
Pour un point M quelconque situé sur la courbe, son symétrique, par rapport à O l’origine du repère, M’ est lui aussi situé sur la courbe. On dit que l’origine du repère est centre de symétrie de la courbe de la fonction cube.
Représentation tableur
Voici le tableur de la calculatrice TI-83 pour la fonction cube.

On constate dans ce tableau de valeurs que -5 et 5 ont des images opposées -125 et 125, qu’il en va de même pour -4 et 4 qui ont des images opposées -64 et 64……
Représentation algébrique
La fonction cube est définie sur \mathbf{R}.
Si x \in\mathbf{R} alors -x \in\mathbf{R} et (-x)^3=-x^3 .
On dit que la fonction cube est impaire.
Fonction affine.
Exemple n°1 : \textbf{a>0}
f(x)=0.5x+2
représentation graphique
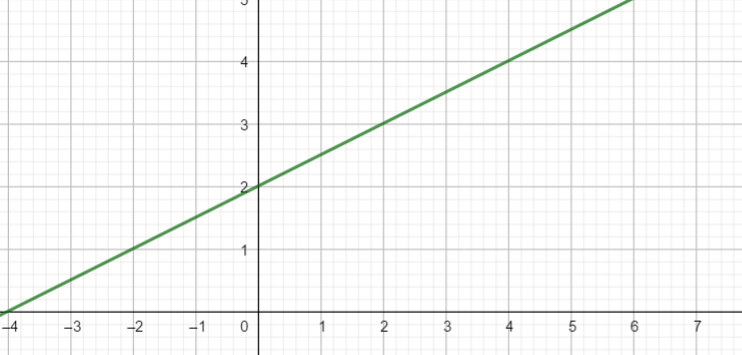
L’axe des ordonnées n’est pas axe de symétrie et l’origine du repère n’est pas centre de symétrie.
représentation tableur
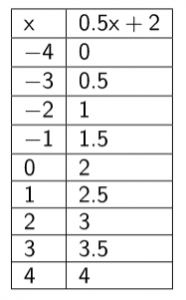
Un nombre et son opposé ont des images qui ne sont ni égales, ni opposées.
représentation algébrique
f(x)=0.5x+2 définie sur \mathbb{R}
Si x \in\mathbf{R} alors -x \in\mathbf{R} mais si on calcule f(-x), on ne trouve ni f(x), ni -f(x). Donc f n’est ni paire, ni impaire.
Exemple n°2 : \textbf{a<0}
f(x)=-2x+4
représentation graphique
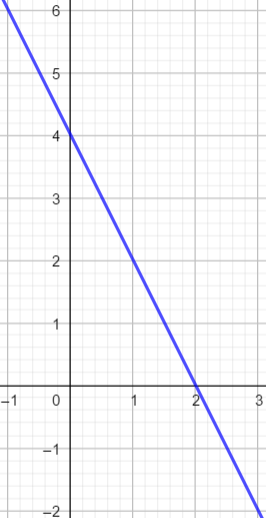
L’axe des ordonnées n’est pas axe de symétrie et l’origine du repère n’est pas centre de symétrie.
représentation tableur
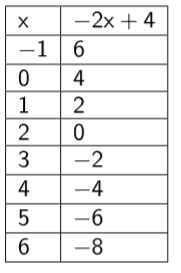
Un nombre et son opposé ont des images qui ne sont ni égales, ni opposées.
représentation algébrique
f(x)=-2x+4 définie sur \mathbb{R}
Si x \in\mathbf{R} alors -x \in\mathbf{R} mais si on calcule f(-x), on ne trouve ni f(x), ni -f(x). Donc f n’est ni paire, ni impaire.
fonction inverse
représentation graphique
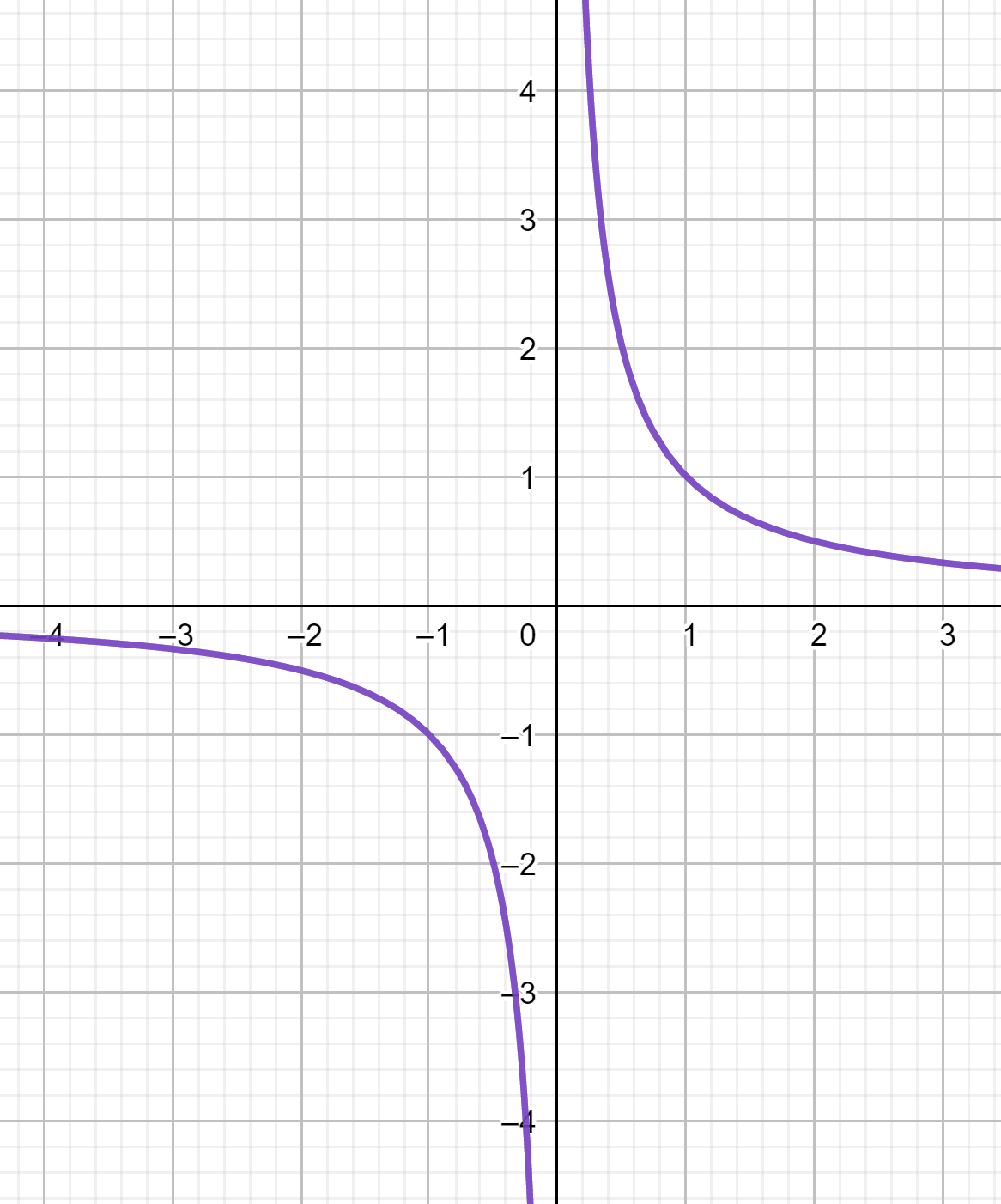
Pour un point M quelconque situé sur la courbe, son symétrique, par rapport à O l’origine du repère, M’ est lui aussi situé sur la courbe. On dit que l’origine du repère est centre de symétrie de la courbe de la fonction cube.
représentation tableur
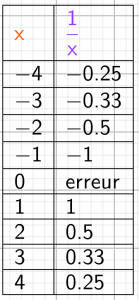
On constate dans ce tableau de valeurs que -4 et 4 ont des images opposées -0.25 et 0.25, qu’il en va de même pour -2 et 2 qui ont des images opposées -0.5 et 0.5……
représentation algébrique
f(x)=\frac{1}{x} définie sur
\mathbf{R} privé de 0 noté aussi \mathbf{R}* .
Si x \in\mathbf{R}* alors -x \in\mathbf{R}* et f(-x)=\frac{1}{(-x)}=-\frac{1}{x}=-f(x) .
On dit que la fonction inverse est impaire.
fonction racine carrée
représentation graphique
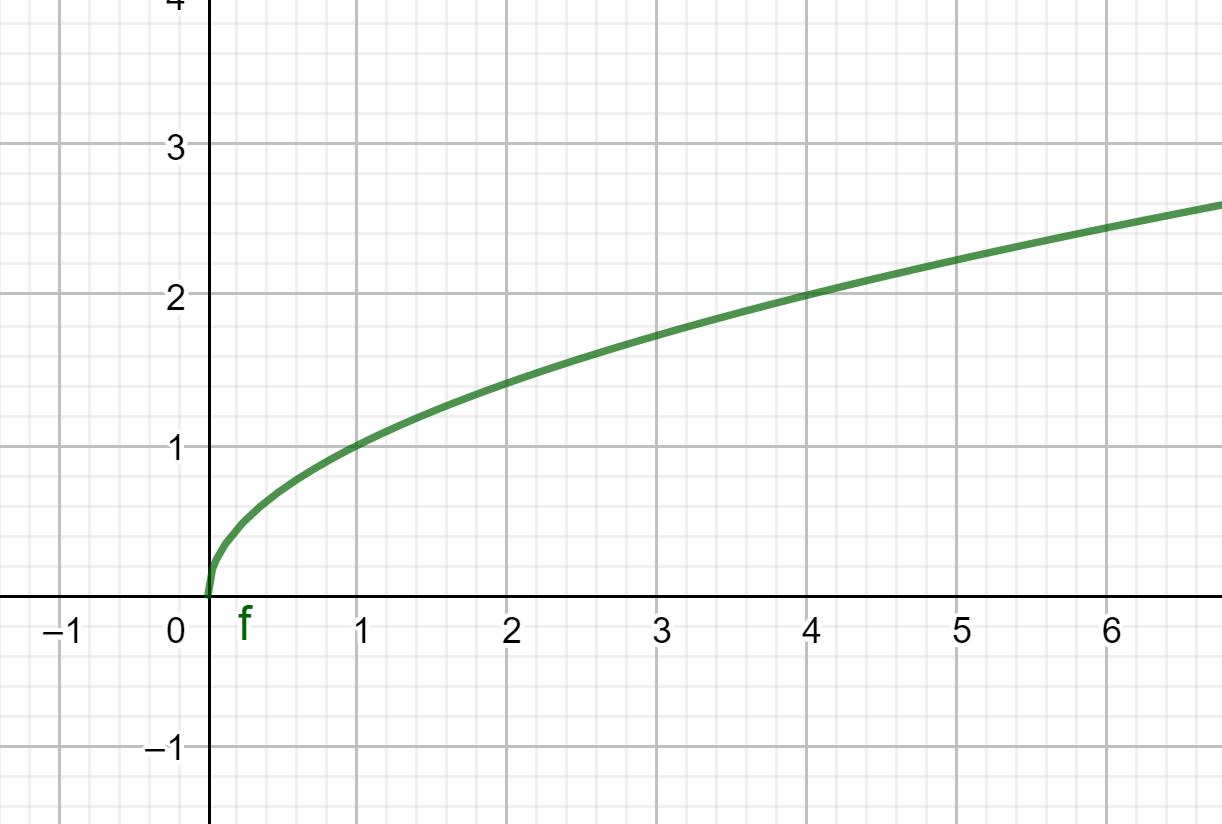
L’axe des ordonnées n’est pas axe de symétrie et l’origine du repère n’est pas centre de symétrie.
représentation tableur
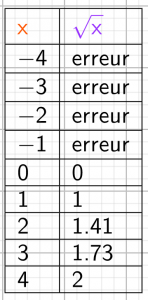
Ici on ne peut pas comparer les images de deux nombres opposés car seuls les nombres positifs ont une image.
représentation algébrique
f(x)=\sqrt{x} définie sur [0;+\infty[
Si x \in[0;+\infty[ mais -x \notin[0;+\infty[, il n’est donc pas nécessaire de calculer f(-x) .
La fonction racine carrée n’est ni paire, ni impaire .
Définitions et propriétés :
Fonctions paires
définition 1 : Soit f une fonction définie sur un ensemble D, on dit que la fonction est paire si :
pour tout x\in D,-x\in D et f(-x)=f(x).
Propriété 1 : Si fest une fonction paire alors l’axe des ordonnées est axe de symétrie de la courbe représentative de la fonction f dans un repère orthogonal.
Fonctions impaires
définition 2 : Soit f une fonction définie sur un ensemble D, on dit que la fonction est impaire si :
pour tout x\in D,-x\in D et f(-x)=-f(x).
Propriété 2 : Si fest une fonction impaire alors l’origine du repère est centre de symétrie de la courbe représentative de la fonction f dans un repère donné.
Exercices
Exercice résolu : Soit f la fonction définie sur \mathbf{R} par f(x)=\frac{x}{x^2+1}. Etudier la parité de f.
METHODE :
Etape n°1 : S’assurer que l’ensemble sur lequel est définie f est symétrique par rapport à 0 (zéro), c’est-à-dire s’assurer que si x\in D,-x\in D.
si x\in \mathbf{R} alors -x\in \mathbf{R}
Etape n°2: On calcule f(-x) en remplaçant x par (-x) entre parenthèses dans f(x)=….
Si on trouve f(x), la fonction est paire.
Si on trouve -f(x), la fonction est impaire.
Si on trouve ni f(x), ni -f(x), fonction n’est ni paire, ni impaire.
f(-x)=\frac{(-x)}{(-x)^2+1}\\\hspace{1cm}=\frac{(-x)}{x^2+1}\\f(-x)=-\frac{x}{x^2+1}\\f(-x)=-f(x)Donc la fonction f est impaire.
Exercice :
1.f(x)=x^4+2x^2+2 sur \mathbf{R}
2.f(x)=3x^3+x sur \mathbf{R}
3.f(x)=\sqrt{x^2+2} sur \mathbf{R}
4.f(x)=\frac{x+4}{x^2} sur \mathbf{R}*
5.f(x)=\frac{5x^2}{x^3+x} sur \mathbf{R}*
6.f(x)=5x sur \mathbf{R}
Page géogébra pour valider
Validation avec la page Géogébra ci-dessous. Tracer la courbe dans chaque cas et regarder si la courbe a l’axe des ordonnées pour axe de symétrie ( fonction paire ) , si la courbe a l’origine pour centre de symétrie ( fonction impaire) ou si la courbe n’a pas l’axe des ordonnées pour axe de symétrie (pas paire) et n’a pas l’origine pour centre de symétrie (pas impaire) .



