Soient A et B deux points tels que la distance AB=8.
Soit M, un point variable sur le segment [AB].
On construit le carré AMNP et le triangle MQB rectangle et isocèle en Q.
Où placer le point M sur le segment [AB] pour que les aires du carré AMNP et du triangle MQB soient égales ?
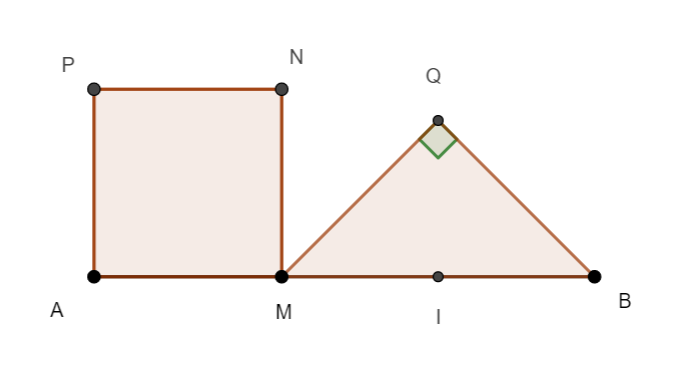
Résolution géométrique avec Géogébra.
a. Faire la figure à l’aide du logiciel géogébra.
b. Répondre au problème posé à l’aide du logiciel géogébra.
Résolution algébrique.
On veut déterminer la distance AM . Comme on ne la connaît pas on la note x. Ainsi AM=x. On remarque que x\in [0;8].
- Exprimer l’aire du carré AMNP en fonction de x.
2. Le but de cette question est d’exprimer l’aire du triangle MQB en fonction de x.
a. Démontrer que IM=IQ=IB .
b. Démontrer que les droites (IQ) et (MB sont perpendiculaires. En déduire que (IQ) est une hauteur dans le triangle MQB .
c. A l’aide des questions précédentes, exprimer l’aire du triangle MQB en fonction de x.
3. Résoudre l’équation du second degré suivante x^2=(\frac{8-x}{2})^2 dans l’intervalle [0;8]. Puis répondre à la question posée dans le problème.



