logo

1. signe du polynôme du 2nd degré.Exercices.

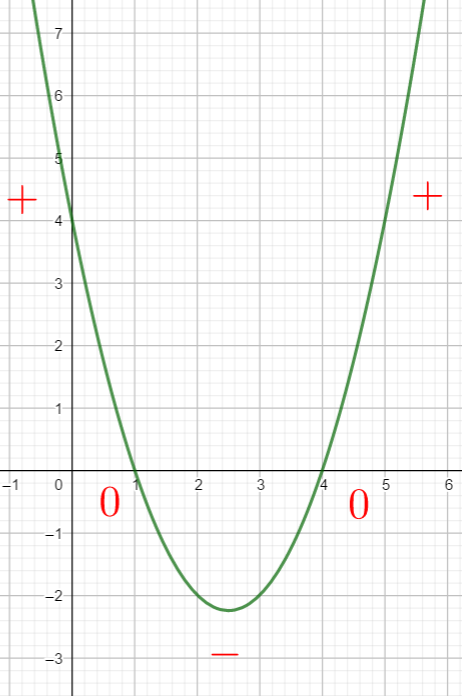
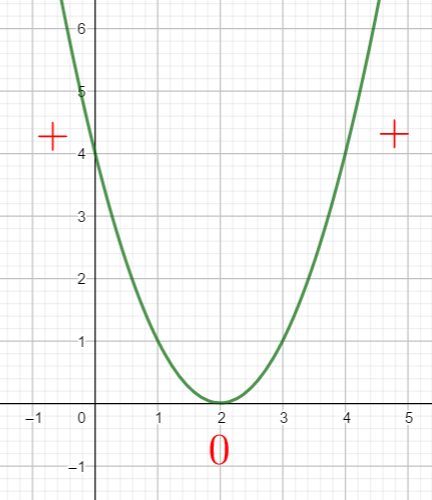
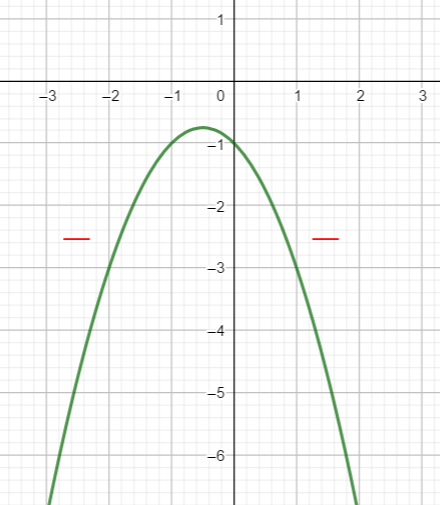
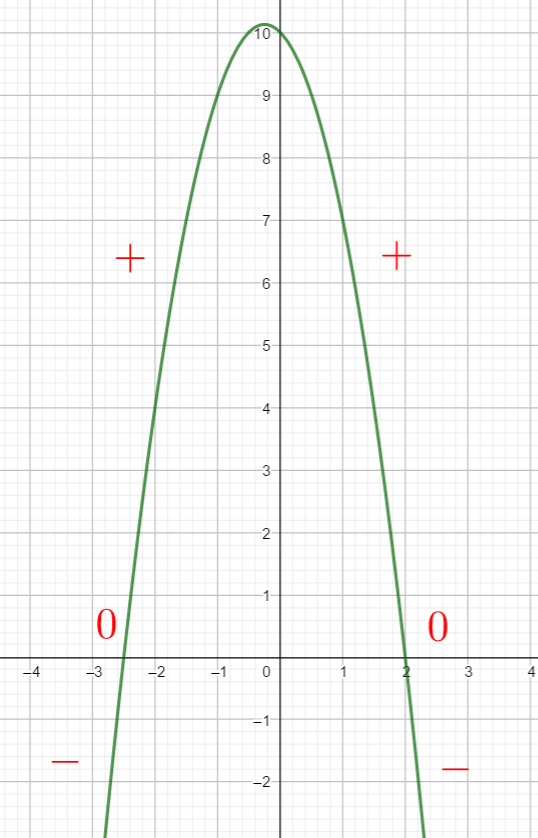
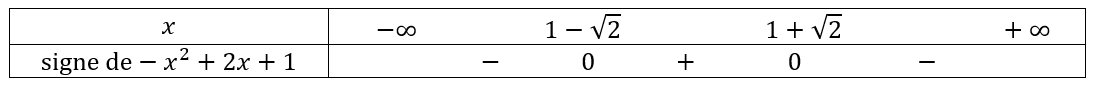Un petit conseil, avant de vous lancer dans le calcul de \Delta, faire une conjecture graphique en utilisant la fenêtre Géogébra ci-dessous . N’hésitez pas à déplacer le graphique et à utiliser Agrandissement et Réduction pour faire apparaître les points d’intersection de la courbe et de l’axe des abscisses.

Pour cela saisir par exemple f(x)=x^2-5x+4   dans la colonne de gauche et regarder quand la courbe est au-dessus de l’axe des abscisses et quand la courbe est en-dessous de l’axe des abscisses.

Exercice

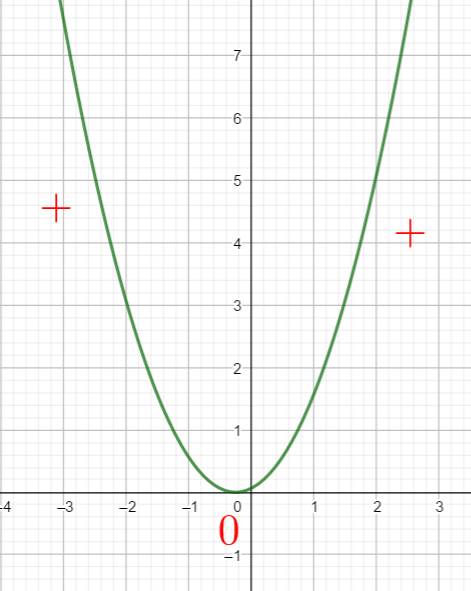
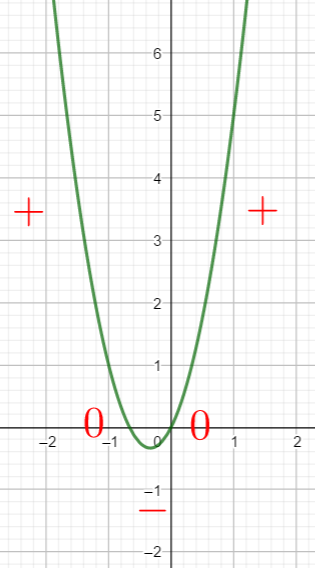
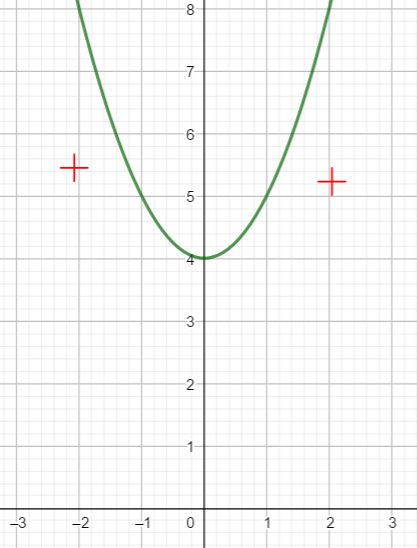
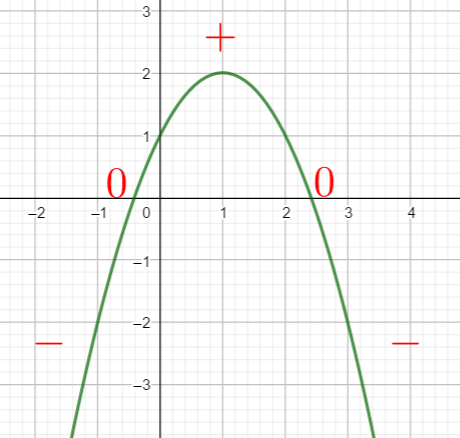
En utilisant le théorème du cours étudier le signe des fonctions polynômes du second degré suivants :

  1. f(x)=x^2-5x+4
conjecture graphique
correction
vidéo de la correction

2. f(x)=x^2-4x+4

conjecture graphique
correction
vidéo de la correction

3. f(x)=-x^2-x-1

conjecture graphique
correction
vidéo de la correction

4. f(x)=-2x^2-x+10

conjecture graphique
correction

5. f(x)=x^2+\frac{1}{2}x+\frac{1}{16}

conjecture graphique
correction

6. f(x)=3x^3+2x

conjecture graphique
correction

7. f(x)=x^2+4

conjecture graphique
correction

8. f(x)=-x^2+2x+1

conjecture graphique
correction

Pour valider votre réponse, utiliser la page Calcul Formel de Géogébra ci-dessous:

3. Vérification à l’aide de l’application Calcul Formel de Géogébra.

On peut par exemple chercher pour quelles valeurs de x le polynôme est de signe + puis on compare avec le résultat obtenu.

Pour cela saisir par exemple x^2-5x+4 >0 sur la ligne n°1 et cliquer sur 7ème onglet (X=) en haut à partir de la gauche.

La réponse qui apparait est {x<1,x>4} 

©2020 – Math’O karé SAS

Conjecture graphique :

Pour déterminer graphiquement le signe de x^2-5x+4

Je parcours la courbe avec mon index de la gauche vers la droite en disant positif si la courbe de la fonction  f est au dessus de l’axe des abscisses  et en disant négatif si la courbe de la fonction  f est en-dessous de l’axe des abscisses

La fonction polynôme est de signe + à l’extérieur des racines  1 et 4 et est de signe – à l’intérieur des racines  1 et 4. Elle s’annule pour les valeurs 1 et 4.

 

 Etude du signe de x^2-5x+4 par le calcul en utilisant le théorème plus haut.

J’identifie les coefficients l’équation a=1, b=-5 et c=4.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1, (-5) ,4  .

\Delta=(-5)²-4\times{1}\times{4}\\\Delta=25-16\\\Delta=9

Comme \Delta>0 , l’équation admet deux solutions réelles notées

x_1=\frac{-b-\sqrt{\Delta}}{2a} et x_2=\frac{-b+\sqrt{\Delta}}{2a}.

et ax²+bx+c est  du signe de a à l’extérieur des racines et du signe de (-a) à l’intérieur des racines.

Je calcule x_1=\frac{-b-\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par 1, (-5), 9.

x_1=\frac{-(-5)-\sqrt{9}}{2\times{1}}\\x_1=\frac{5-3}{2}\\x_1=\frac{2}{2}\\x_1=1

Je calcule x_2=\frac{-b+\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par 1, (-5)  , 9.

x_2=\frac{-(-5)+\sqrt{9}}{2\times{1}}\\x_2=\frac{5+3}{2}\\x_2=\frac{8}{2}\\x_2=4

Je dresse le tableau de signes du polynôme:

Comme a=1 le signe de a est positif.

 

 

 

Conjecture graphique :

Pour déterminer graphiquement le signe de f(x)=x^2-4x+4

Je parcours la courbe avec mon index de la gauche vers la droite en disant positif si la courbe de la fonction  f est au dessus de l’axe des abscisses  et en disant négatif si la courbe de la fonction  f est en-dessous de l’axe des abscisses

La fonction polynôme est toujours de  signe + . Elle s’annule pour la valeur 2 .

 

 

 Etude du signe de f(x)=x^2-4x+4 par le calcul en utilisant le théorème plus haut.

J’identifie les coefficients  a=1, b=-4 et c=4.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1, (-4), 4  .

\Delta=(-4)²-4\times{1}\times{4}\\\Delta=16-16\\\Delta=0

comme  \Delta=0, ax²+bx+c est toujours du signe de a et s’annule pour x_0=-\frac{b}{2a}

Je calcule x_0=-\frac{b}{2a} en remplaçant a,b  par 1, (-4).

x_0=-\frac{(-4)}{2\times{1}}\\x_0=\frac{4}{2}\\x_0=2

Je dresse le tableau de signes de la fonction polynôme.

Comme a=1 le signe de a est positif.

 

 

Conjecture graphique :

Pour déterminer graphiquement le signe de f(x)=-x^2-x-1

Je parcours la courbe avec mon index de la gauche vers la droite en disant positif si la courbe de la fonction  f est au dessus de l’axe des abscisses  et en disant négatif si la courbe de la fonction  f est en-dessous de l’axe des abscisses

La fonction polynôme est toujours de signe – . De plus, elle ne  s’annule jamais.

 

 

 Etude du signe de -x^2-x-1 par le calcul en utilisant le théorème.

J’identifie les coefficients l’équation a=-1, b=-1 et c=-1.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par (-1),(-1),(-1)  .

\Delta=(-1)²-4\times{(-1)}\times{(-1)}\\\Delta=1-4\\\Delta=-3

comme \Delta<0 , ax²+bx+c est toujours du signe de a.

Comme a=-1,  -x^2-x-1 est toujours du signe –.

 

 

 

Conjecture graphique :

Pour déterminer graphiquement le signe de f(x)=-2x^2-x+10

Je parcours la courbe avec mon index de la gauche vers la droite en disant positif si la courbe de la fonction  f est au dessus de l’axe des abscisses  et en disant négatif si la courbe de la fonction  f est en-dessous de l’axe des abscisses

La fonction polynôme est de signe – à l’extérieur des racines  -2.5 et 3 et est de signe + à l’intérieur des racines  -2.5 et 3. Elle s’annule pour les valeurs -2.5 et 2.

 

 Etude du signe de la fonction polynôme  f(x)=-2x^2-x+10 par le calcul en utilisant le théorème .

J’identifie les coefficients l’équation a=-2, b=-1 et c=10.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par (-2), (-1) ,10  .

\Delta=(-1)²-4\times{(-2)}\times{10}\\\Delta=1+80\\\Delta=81

Comme \Delta>0 , l’équation admet deux solutions réelles notées

x_1=\frac{-b-\sqrt{\Delta}}{2a} et x_2=\frac{-b+\sqrt{\Delta}}{2a}.

et ax²+bx+c est  du signe de a à l’extérieur des racines et du signe de (-a) à l’intérieur des racines.

Je calcule x_1=\frac{-b-\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par (-2), (-1), 81.

x_1=\frac{-(-1)-\sqrt{81}}{2\times{(-2)}}\\x_1=\frac{1-9}{-4}\\x_1=\frac{-8}{-4}\\x_1=2

Je calcule x_2=\frac{-b+\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par (-2), (-1), 81.

x_2=\frac{-(-1)+\sqrt{81}}{2\times{(-2)}}\\x_2=\frac{1+9}{-4}\\x_2=\frac{10}{-4}\\x_2=-\frac{5}{2}

Je dresse le tableau de signes du polynôme:

Comme a=-2 le signe de a est négatif.

Attention : ici la plus petite des racines est x_2 donc on met d’abord -\frac{5}{2} puis à sa gauche x_1 c’est-à-dire 2.

 

 

 

Conjecture graphique :

Pour déterminer graphiquement le signe de f(x)=x^2+\frac{1}{2}x+\frac{1}{16}

Je parcours la courbe avec mon index de la gauche vers la droite en disant positif si la courbe de la fonction  f est au dessus de l’axe des abscisses  et en disant négatif si la courbe de la fonction  f est en-dessous de l’axe des abscisses

La fonction polynôme est toujours de signe +. Elle s’annule pour la valeur -0.25 .

 

 

 Etude du signe de f(x)=x^2+\frac{1}{2}x+\frac{1}{16} par le calcul en utilisant le théorème du cours.

J’identifie les coefficients  a=1, b=\frac{1}{2} et c=\frac{1}{16}.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1, \frac{1}{2}, \frac{1}{16}  .

\Delta=(\frac{1}{2})²-4\times{1}\times{\frac{1}{16}}\\\Delta=\frac{1}{4}-\frac{4}{16}\\\Delta=\frac{1}{4}-\frac{1}{4}\\\Delta=0

comme  \Delta=0, ax²+bx+c est toujours du signe de a et s’annule pour x_0=-\frac{b}{2a}

Je calcule x_0=-\frac{b}{2a} en remplaçant a,b  par 1, \frac{1}{2}.

x_0=-\frac{\frac{1}{2}}{2\times{1}}\\x_0=-\frac{\frac{1}{2}}{2}

Diviser par 2 revient à multiplier par son inverse \frac{1}{2}

x_0=-{\frac{1}{2}}\times{\frac{1}{2}}\\x_0=-\frac{1}{4}

Je dresse le tableau de signes de la fonction polynôme.

Comme a=1 le signe de a est positif.

 

 

Conjecture graphique :

Pour déterminer graphiquement le signe de f(x)=3x^2+2x

Je parcours la courbe avec mon index de la gauche vers la droite en disant positif si la courbe de la fonction  f est au dessus de l’axe des abscisses  et en disant négatif si la courbe de la fonction  f est en-dessous de l’axe des abscisses

La fonction polynôme est  de signe + à l’extérieur des racines  -0.7 et 0 et de signe – à l’intérieur des racines  -0.7 et 0. De plus, elle  s’annule pour les valeurs -0.7 et 0.

 

 

 Etude du signe de la fonction polynôme f(x)=3x^2+2x par le calcul en utilisant le théorème du cours.

J’identifie les coefficients l’équation a=3, b=2 et c=0.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 3, 2 ,0  .

\Delta=2²-4\times{3}\times{0}\\\Delta=4-0\\\Delta=4

Comme \Delta>0 , l’équation admet deux solutions réelles notées

x_1=\frac{-b-\sqrt{\Delta}}{2a} et x_2=\frac{-b+\sqrt{\Delta}}{2a}.

et ax²+bx+c est  du signe de a à l’extérieur des racines et du signe de (-a) à l’intérieur des racines.

Je calcule x_1=\frac{-b-\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par 3, 2, 4.

x_1=\frac{-2-\sqrt{4}}{2\times{3}}\\x_1=\frac{-2-2}{6}\\x_1=\frac{-4}{6}

Après simplification par 2

x_1=-\frac{2}{3}

Je calcule x_2=\frac{-b+\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par 3, 2, 4.

x_2=\frac{-2+\sqrt{4}}{2\times{3}}\\x_2=\frac{-2+2}{6}\\x_2=\frac{0}{6}\\x_2=0

Je dresse le tableau de signes de la fonction  polynôme:

Comme a=3 le signe de a est positif.

 

 

 

Conjecture graphique :

Pour déterminer graphiquement le signe de x^2+4

Je parcours la courbe avec mon index de la gauche vers la droite en disant positif si la courbe de la fonction  f est au dessus de l’axe des abscisses  et en disant négatif si la courbe de la fonction  f est en-dessous de l’axe des abscisses

La fonction polynôme est toujours du signe + . Elle ne s’annule jamais.

 

 

 Etude du signe de la fonction polynôme f(x)=x^2+4 par le calcul en utilisant le théorème.

J’identifie les coefficients l’équation a=1, b=0 et c=4.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par 1,0,4  .

\Delta=0²-4\times{1}\times{4}\\\Delta=0-16\\\Delta=-16

comme \Delta<0 , ax²+bx+c est toujours du signe de a.

Comme a=1, la fonction polynôme  f(x)=x^2+4 est toujours du signe +.

Remarque : ce résultat était bien sûr prévisible car x^2+4 est la somme de deux nombres positifs donc positive. 

 

 

 

Conjecture graphique :

Pour déterminer graphiquement le signe de f(x)=-x^2+2x+1

Je parcours la courbe avec mon index de la gauche vers la droite en disant positif si la courbe de la fonction  f est au dessus de l’axe des abscisses  et en disant négatif si la courbe de la fonction  f est en-dessous de l’axe des abscisses

La fonction polynôme est de signe – à l’extérieur des racines  -0.4 et 2.4 et est de signe + à l’intérieur des racines  -0.4 et 2.4. Elle s’annule pour les valeurs -0.4 et 2.4.

 

 

 Etude du signe de la fonction polynôme f(x)=-x^2+2x+1 par le calcul en utilisant le théorème du cours.

J’identifie les coefficients l’équation a=-1, b=2 et c=1.

Je calcule \Delta=b²-4ac  en remplaçant a,b,c  par (-1), 2,1  .

\Delta=2²-4\times{(-1)}\times{1}\\\Delta=4+4\\\Delta=8

Comme \Delta>0 , l’équation admet deux solutions réelles notées

x_1=\frac{-b-\sqrt{\Delta}}{2a} et x_2=\frac{-b+\sqrt{\Delta}}{2a}.

et ax²+bx+c est  du signe de a à l’extérieur des racines et du signe de (-a) à l’intérieur des racines.

Je calcule x_1=\frac{-b-\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par (-1), 2, 8.

x_1=\frac{-2-\sqrt{8}}{2\times{(-1)}}

8 est le produit d’un carré fois un nombre 8=4\times2 donc \sqrt{8}=\sqrt{4\times2}={\sqrt{4}}\times{\sqrt{2}}=2\sqrt{2}

x_1=\frac{-2-2\sqrt{2}}{-2}

On factorise le numérateur par  -2 pour pouvoir ensuite simplifier.

x_1=\frac{-2(1+\sqrt{2})}{-2}

x_1=1+\sqrt{2}

Je calcule x_2=\frac{-b+\sqrt{\Delta}}{2a} en remplaçant a,b,\Delta  par (-1), 2, 8.

x_2=\frac{-2+\sqrt{8}}{2\times{(-1)}}

8 est le produit d’un carré fois un nombre 8=4\times2 donc \sqrt{8}=\sqrt{4\times2}={\sqrt{4}}\times{\sqrt{2}}=2\sqrt{2}

x_2=\frac{-2+2\sqrt{2}}{-2}

On factorise le numérateur par  -2 pour pouvoir ensuite simplifier.

x_2=\frac{-2(1-\sqrt{2})}{-2}

x_2=1-\sqrt{2}

Je dresse le tableau de signes de la fonction  polynôme.

Comme a=-1 le signe de a est négatif

 

 

 

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.