Sommaire
Exemple n°1:
mettre sous forme canonique la fonction polynôme f(x)=-2x^2-8x+1
Méthode par factorisation
Pour mettre -2x^2-8x+1 sous forme canonique, il faut mettre en facteur -2 (c’est le coefficient de x^2) pour les deux premiers termes -2x^2-8x.
J’écris :
-2x^2= -2 \times x^2\\-8x= -2 \times 4xPuis je factorise ainsi :
-2x^2-8x=-2(x^2+4x)Méthode n°1 :
x^2+4x est le début du développement de l’identité remarquable (A+B)^2=A^2+2AB+B^2 avec :
A^2=x^2 donc A=x\\2AB=4x donc B=\frac{4x}{2A}=\frac{4x}{2x}=2.
En remplaçant A et B par x et 2, on obtient :
(x+2)^2=x^2+4x+4ou x^2+4x+4=(x+2)^2
Donc x^2+4x=(x+2)^2-4
Méthode n°2 :
x^2+4x est la somme de l’aire d’un carré et de deux rectangles de dimensions identiques comme ci-dessous :
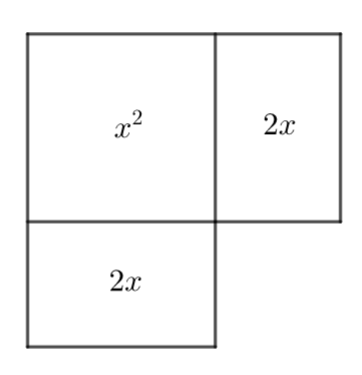
Le côté du carré vaut x et les dimensions des rectangles sont x et 2.
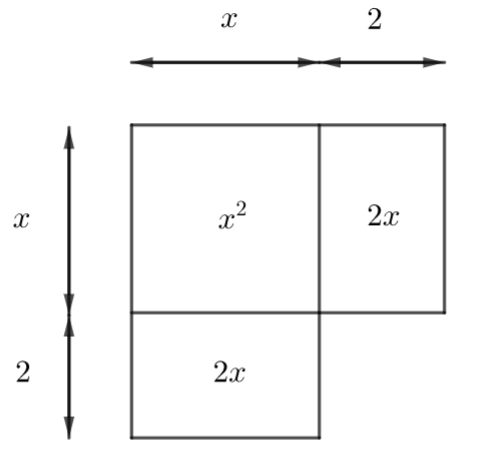
Le côté du grand carré vaut x+2.
Donc l’aire de départ s’obtient en calculant l’aire du grand carré puis en retranchant l’aire du petit carré de côté 2. C’est-à-dire (x+2)^2-2^2 ou (x+2)^2-4.
Donc x^2+4x=(x+2)^2-4
Voilà ce qu’il faut écrire sur la copie :
-2x^2-8x+1=-2(x^2+4x)+1On remplace x^2+4x par (x+2)^2-4\\\hspace {2.3cm}=-2((x+2)^2-4)+1
On développe le produit en utilisant la distributivité de la multiplication par rapport à l’addition.
\hspace {2.3cm}=-2(x+2)^2-2\times{-4}+1\\\hspace {2.3cm}=-2(x+2)^2+8+1\\\hspace {2.3cm}=-2(x+2)^2+9Méthode où on utilise la formule du cours
Pour mettre -2x^2-8x+1 sous forme canonique, on identifie les coefficients a=-2 , b=-8 et c=1 puis on remplace a, b, c par (-2), (-8), 1 dans :
ax^2+bx+c=a(x+\frac{b}{2a})^2-\frac{b^2-4ac}{4a}\\-2x^2-8x+1=-2(x+\frac{(-8)}{2\times(-2)})^2-\frac{(-8)^2-4\times (-2)\times1}{4\times(-2)}\\-2x^2-8x+1=-2(x+\frac{(-8)}{(-4)})^2-\frac{64+8}{(-8)}\\-2x^2-8x+1=-2(x+2)^2-\frac{72}{(-8)}\\-2x^2-8x+1=-2(x+2)^2+9
Exemple n°2:
mettre sous forme canonique la fonction polynôme f(x)=3x^2-12x+5
Méthode par factorisation
Pour mettre 3x^2-12x+5 sous forme canonique, il faut mettre en facteur 3 (c’est le coefficient de x^2) pour les deux premiers termes 3x^2-12x.
J’écris :
3x^2= 3 \times x^2\\-12x= 3 \times (-4x)Puis je factorise ainsi :
3x^2-12x=3(x^2-4x)Méthode n°1 :
x^2-4x est le début du développement de l’identité remarquable (A-B)^2=A^2-2AB+B^2 avec :
A^2=x^2 donc A=x\\2AB=4x donc B=\frac{4x}{2A}=\frac{4x}{2x}=2.
En remplaçant A et B par x et 2, on obtient :
(x-2)^2=x^2-4x+4ou x^2-4x+4=(x-2)^2
Donc x^2-4x=(x-2)^2-4
Méthode n°2 :
Par formule, l’aire du carré de côté x vaut x^2 .
Par découpage, l’aire du carré de côté x vaut l’aire du carré blanc (x-2)^2 plus les aires des deux rectangles de dimensions x et 2 moins l’aire du petit carré colorié deux fois (que l’on a compté deux fois).
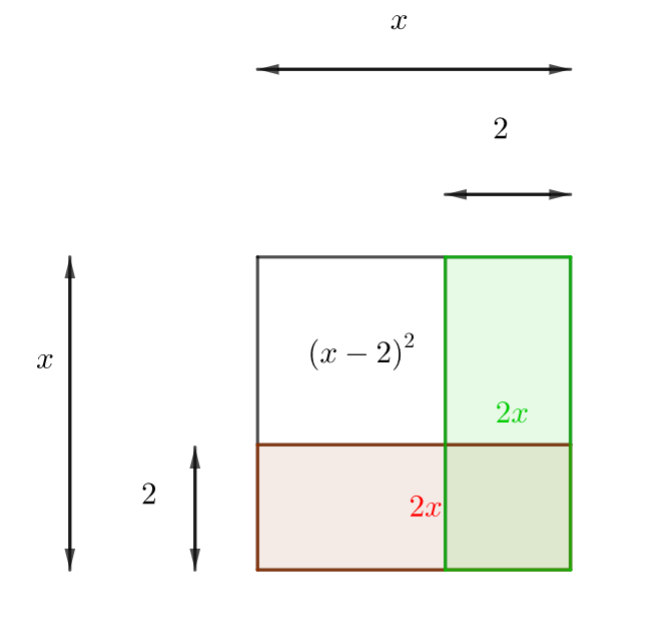
Donc x^2=(x-2)^2+4x-4
ou x^2-4x=(x-2)^2-4
Voilà ce qu’il faut écrire sur la copie :
3x^2-12x+5=3(x^2-4x)+5
Comme x^2-4x=(x-2)^2-4, je remplace x^2-4x par (x-2)^2-4.
\hspace{2.2cm}=3((x-2)^2-4)+5
On développe le produit en utilisant la distributivité de la multiplication par rapport à l’addition.
\hspace{2.2cm}=3(x-2)^2-3\times {4}+5
\hspace{2.2cm}=3(x-2)^2-12+5
On réduit.
\hspace{2.2cm}=3(x-2)^2-7
Méthode où on utilise la formule du cours
Pour mettre 3x^2-12x+5 sous forme canonique, on identifie les coefficients a=3 , b=-12 et c=5 puis on remplace a, b, c par 3, (-12), 5 dans :
ax^2+bx+c=a(x+\frac{b}{2a})^2-\frac{b^2-4ac}{4a}\\3x^2-12x+5=3(x+\frac{(-12)}{2\times 3})^2-\frac{(-12)^2-4\times 3\times5)}{4\times 3}\\\hspace{2.2cm}=3(x+\frac{(-12)}{6})^2-\frac{144-60}{12}\\\hspace{2.2cm}=3(x-2)^2-\frac{84}{12}\\\hspace{2.2cm}=3(x-2)^2-7



