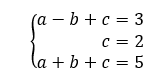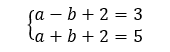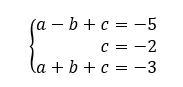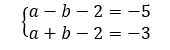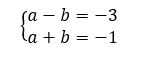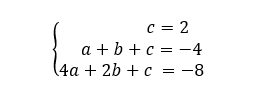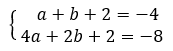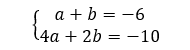Sommaire
Exemple n°1 : déterminer graphiquement la forme factorisée d’une fonction polynôme du second degré
Voici la courbe d’une fonction polynôme du 2nd degré.
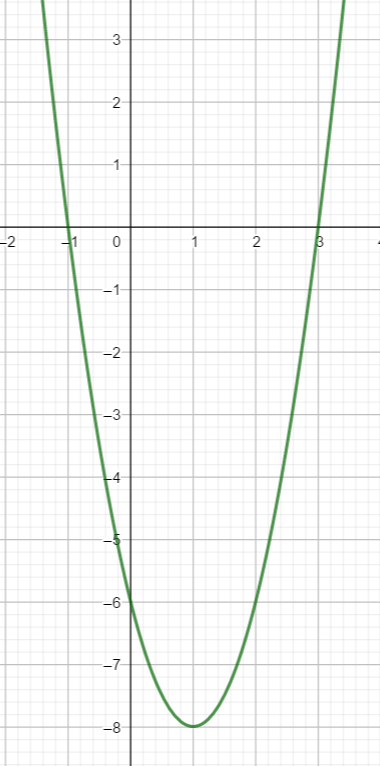
On va déterminer à l’aide du graphique une expression algébrique f(x) de la fonction polynôme du 2nd degré représentée par cette courbe.
On choisit sa forme factorisée car on peut déterminer facilement les deux racines de la fonction polynôme . Ce sont -1 et 3.
L’écriture factorisée est de la forme f(x)=a(x-x_1)(x-x_2) avec x_1=-1 et x_2=3 . Il ne reste plus qu’à déterminer a .
f(x)=a(x-(-1))(x-3)\\f(x)=a(x+1)(x-3)On a déjà utilisé les deux points de la courbe de coordonnées (-1;0) et (3;0), il en faut un autre pour déterminer a. Prenons, par exemple, le point de coordonnées (0;-6).
Le point de coordonnées (0;-6) est sur la courbe donc ses coordonnées vérifient f(0)=-6.
Pour exprimer f(0) en fonction de a, on remplace x par 0 dans l’ écriture f(x)=a(x+1)(x-3) et on obtient f(0)=a(0+1)(0-3). Puis on remplace f(0) par a(0+1)(0-3) dans f(0)=-6.
a(0+1)(0-3)=-6\\a\times1\times(-3)=-6\\-3a=-6\\a=\frac{-6}{-3}\\a=2Donc l’écriture algébrique de f(x) cherchée est :
f(x)=2(x+1)(x-3).
Exercice n°1
Voici la courbe d’une fonction polynôme du 2nd degré
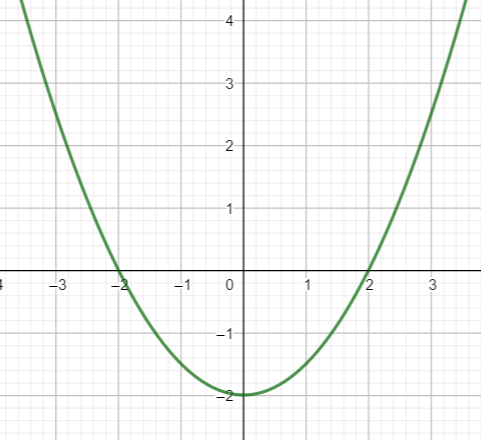
On va déterminer à l’aide du graphique une expression algébrique f(x) de la fonction représentée par cette courbe. On choisira la forme factorisée.
Exercice n°2
Voici la courbe d’une fonction polynôme du 2nd degré
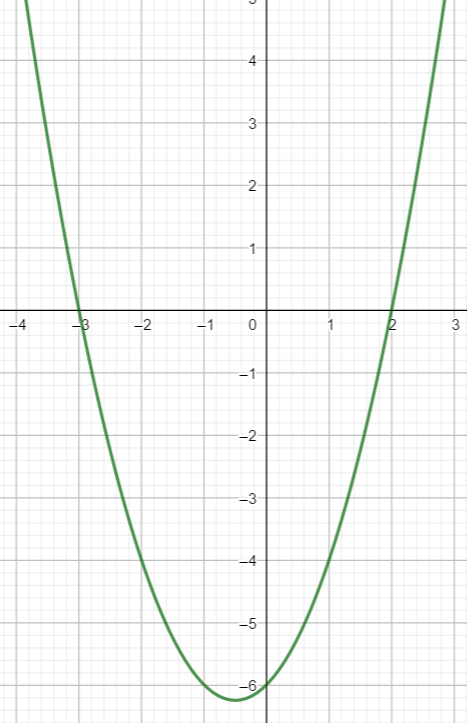
On va déterminer à l’aide du graphique une expression algébrique f(x) de la fonction représentée par cette courbe. On choisira la forme factorisée.
Exercice n°3
Voici la courbe d’une fonction polynôme du 2nd degré
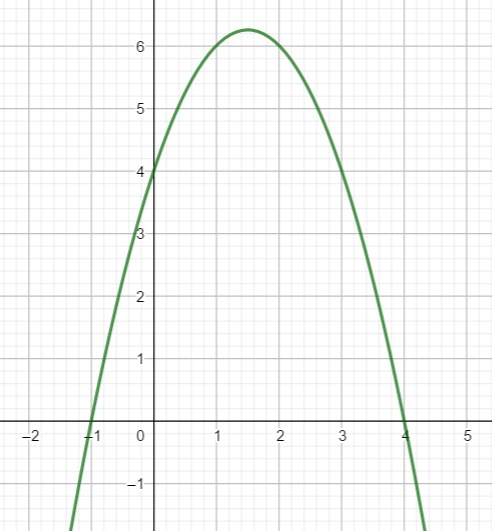
On va déterminer à l’aide du graphique une expression algébrique f(x) de la fonction représentée par cette courbe. On choisira la forme factorisée.
Exemple n°2 : déterminer graphiquement la forme canonique d’une fonction polynôme du second degré
Voici la courbe d’une fonction polynôme du 2nd degré.
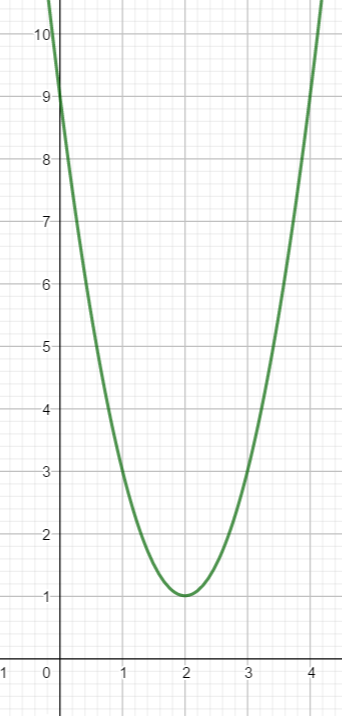
On va déterminer à l’aide du graphique une expression algébrique f(x) de la fonction polynôme du 2nd degré représentée par cette courbe.
On choisit sa forme canonique car on peut déterminer facilement les deux coordonnées du sommet de la parabole qui sont (2;1)
L’écriture canonique est de la forme f(x)=a(x-\alpha)^2+\beta avec \alpha=2 et \beta=1 . Il ne reste plus qu’à déterminer a .
f(x)=a(x-2)^2+1Il faut un point de la courbe pour déterminer a. Prenons, par exemple, le point de coordonnées (0;9).
Le point de coordonnées (0;9) est sur la courbe donc ses coordonnées vérifient f(0)=9.
Pour exprimer f(0) en fonction de a, on remplace x par 0 dans l’ écriture f(x)=a(x-2)^2+1 et on obtient f(0)=a(0-2)^2+1. Puis on remplace f(0) par a(0-2)^2+1 dans f(0)=9.
a(0-2)^2+1=9
a(-2)^2+1=9
4a+1=9
4a=9-1
4a=8
a=\frac{8}{4}\\a=2Donc l’écriture algébrique de f(x) cherchée est :
f(x)=2(x-2)^2+1.
Exercice n°4
Voici la courbe d’une fonction polynôme du 2nd degré
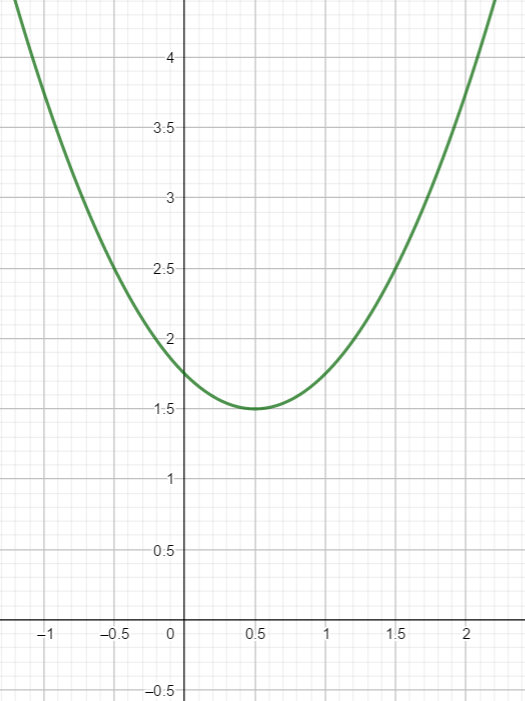
On va déterminer à l’aide du graphique une expression algébrique f(x) de la fonction représentée par cette courbe. On choisira la forme canonique.
Exercice n°5
Voici la courbe d’une fonction polynôme du 2nd degré
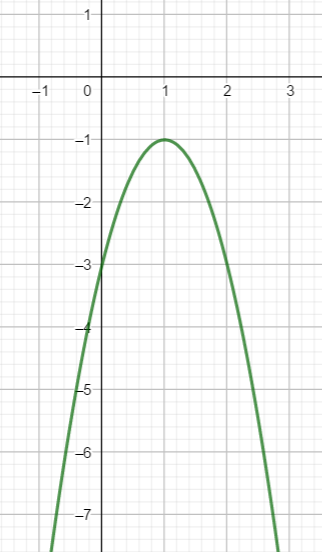
On va déterminer à l’aide du graphique une expression algébrique f(x) de la fonction représentée par cette courbe. On choisira la forme canonique.
Exercice n°6
Voici la courbe d’une fonction polynôme du 2nd degré
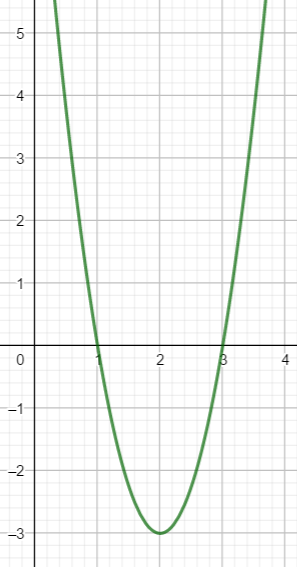
On va déterminer à l’aide du graphique une expression algébrique f(x) de la fonction représentée par cette courbe. On choisira la forme canonique.
Exemple n°3 : déterminer graphiquement la forme développée d’une fonction polynôme du second degré
Voici la courbe d’une fonction polynôme du 2nd degré.
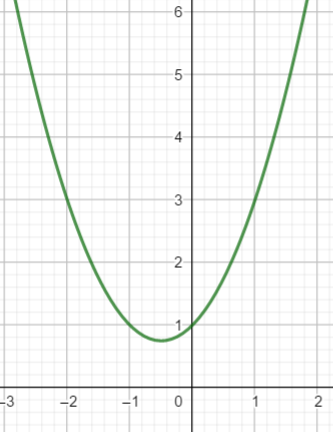
On va déterminer à l’aide du graphique une expression algébrique f(x) de la fonction polynôme du 2nd degré représentée par cette courbe.
On choisit sa forme développée .
L’écriture développée est de la forme f(x)=ax^2+bx+c. Il y a trois inconnues, on doit donc déterminer trois équations ou encore trouver trois points situés sur la courbe dont les coordonnées sont facilement lisibles et plutôt simples.
Les coordonnées des trois points sont, par exemple : (-1;1) , (0;1) et (1;3).
Le point de coordonnées (-1;1) est sur la courbe donc ses coordonnées vérifient f(-1)=1.
Pour exprimer f(-1) en fonction de a, b, c, on remplace x par -1 dans l’ écriture f(x)=ax^2+bx+c et on obtient f(-1)=a(-1)^2+b\times(-1)+c. Puis on remplace f(-1) par a(-1)^2+b\times(-1)+c dans f(-1)=1.
a(-1)^2+b\times(-1)+c=1\\a\times 1-b+c=1\\a-b+c=1 , voici la première équation.
Le point de coordonnées (0;1) est sur la courbe donc ses coordonnées vérifient f(0)=1.
Pour exprimer f(0) en fonction de a, b, c, on remplace x par 0 dans l’ écriture f(x)=ax^2+bx+c et on obtient f(0)=a\times 0^2+b\times0+c. Puis on remplace f(0) par a\times0^2+b\times0+c dans f(0)=1.
a\times0^2+b\times0+c=1
a\times 0+c=1\\c=1 , voici la deuxième équation.
Le point de coordonnées (1;3) est sur la courbe donc ses coordonnées vérifient f(1)=3.
Pour exprimer f(1) en fonction de a, b, c, on remplace x par 1 dans l’ écriture f(x)=ax^2+bx+c et on obtient f(1)=a\times1^2+b\times1+c. Puis on remplace f(1) par a\times1^2+b\times1+c dans f(1)=3.
a\times1^2+b\times1+c=3\\a\times 1+b+c=3\\a+b+c=3 , voici la troisième équation.
On obtient donc le système suivant :
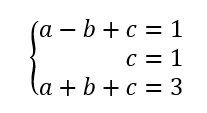
En réalité il n’y a pas trois inconnues car c=1. On remplace c par 1 dans la première et la troisième équation et on obtient le système de deux équations à deux inconnues suivant.
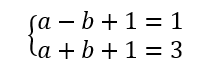
On réduit les écritures
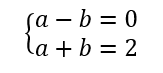
En ajoutant membre à membre ces deux égalités, les b disparaissent et on obtient une équation du premier degré avec l’inconnue a .
a-b+a+b=0+2
2a=2
a=\frac{2}{2}
a=1
Pour déterminer b, on remplace a par la valeur trouvée 1 dans par exemple, l’équation a-b=0.
1-b=0\\-b=-1\\b=1.
On remplace a, b et c par les valeurs qu’on a trouvées : 1, 1 et 1 dans f(x)=ax^2+bx+c.
L’écriture algébrique de f(x) cherchée est f(x)=x^2+x+1
Exercice n°7
Voici la courbe d’une fonction polynôme du 2nd degré
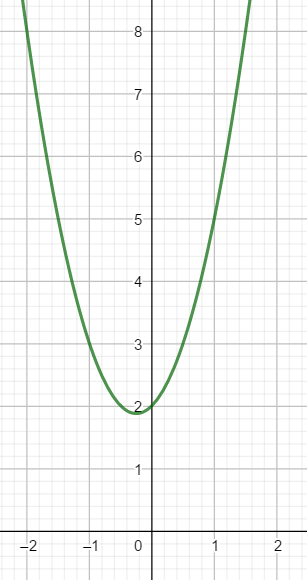
On va déterminer à l’aide du graphique une expression algébrique f(x) de la fonction représentée par cette courbe. On choisira la forme développée.
Exercice n°8
Voici la courbe d’une fonction polynôme du 2nd degré
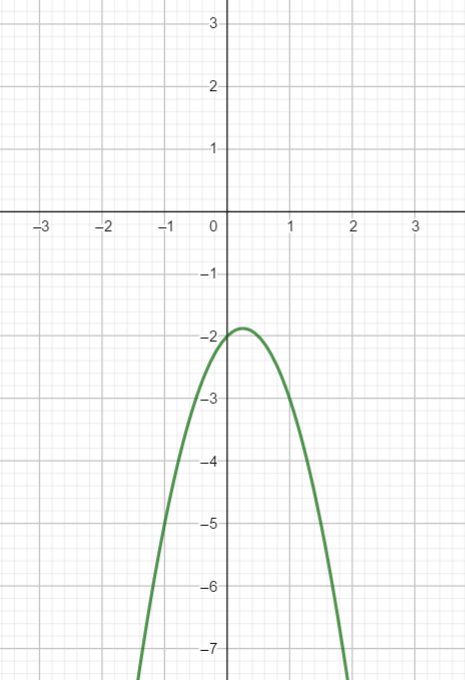
On va déterminer à l’aide du graphique une expression algébrique f(x) de la fonction représentée par cette courbe. On choisira la forme développée.
Exercice n°9
Voici la courbe d’une fonction polynôme du 2nd degré
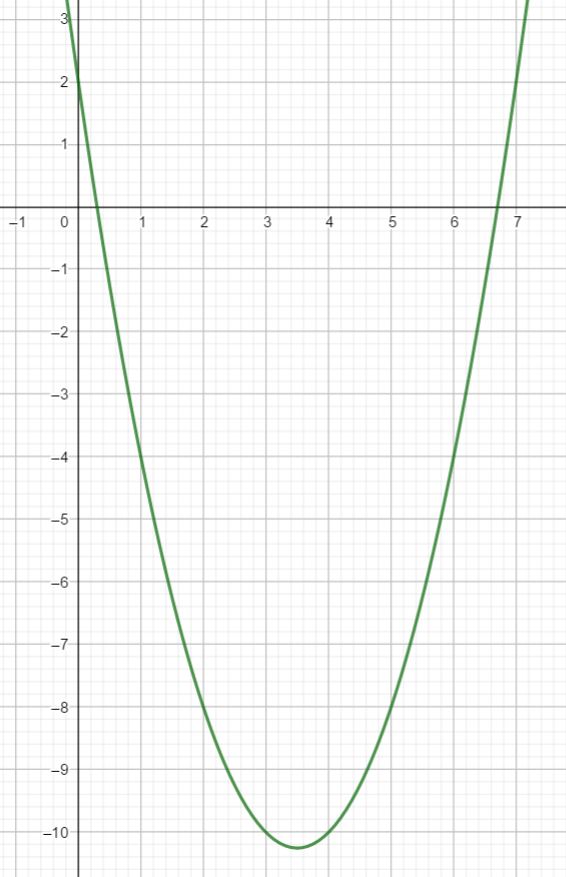
On va déterminer à l’aide du graphique une expression algébrique f(x) de la fonction représentée par cette courbe. On choisira la forme développée.