Sommaire
Exercice n°1 (calculs de termes, algorithme, somme)
Début mars 2020, la France produisait 3.5 millions de masques par semaine. Il fallait alors miser sur une augmentation de 16% pour atteindre une production de 20 millions de masques par semaine fin mai 2020.
On modélise le nombre de masques produits par une suite (u_n) où u_n représente le nombre de masques fabriqués la nième semaine à partir de début mars 2020 (exprimé en millions).
On a donc u_0=3.5.
- Calculer u_1 et u_2. Interpréter ces résultats dans le contexte de l’exercice.
2. Ecrire, pour tout entier naturel n , l’expression de u_n en fonction de n. Calculer ensuite u_{12} et vérifier que l’objectif est atteint.
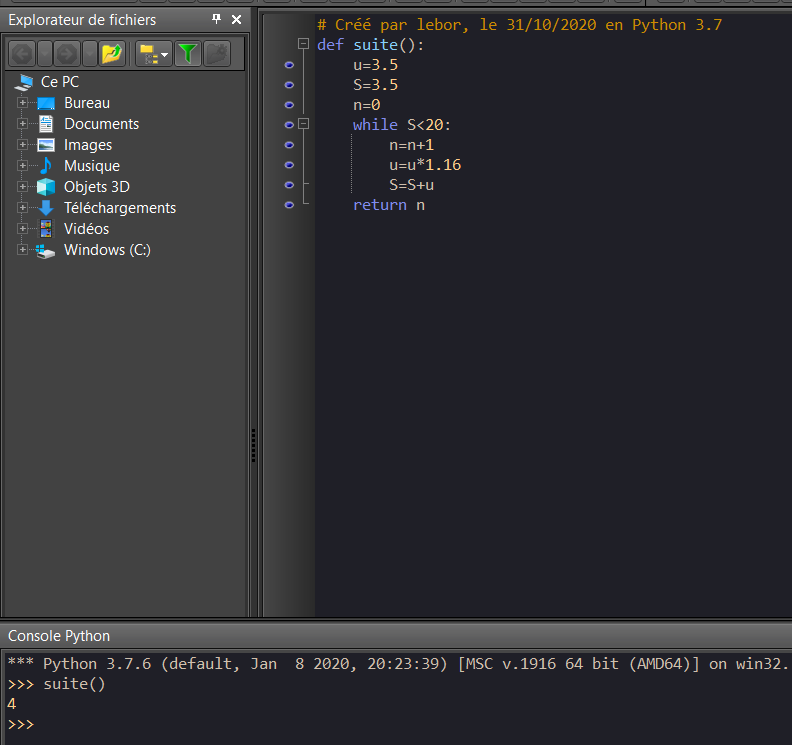
3. Voici un programme rédigé en langage Python:
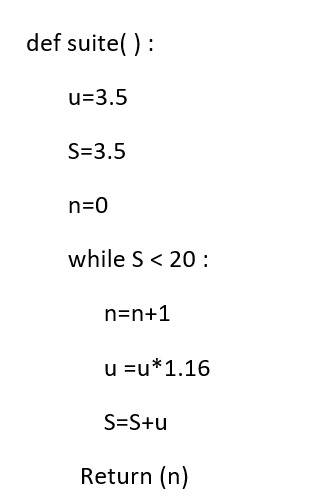
Quelle valeur est retournée par le programme ? Interpréter ce résultat dans le contexte de l’exercice.
4) Calculer u_1+u_2+…u_8 et en déduire le nombre total de masques produits pendant les huit premières semaines.
Exercice n°2 (calculs de termes, algorithme, somme)
Partie A :
Soit (u_n) une suite géométrique de premier terme u_0=1 et de raison 2.
- Calculer u_{8} et u_{14}.
2. Calculer u_0 +u_1+u_2+…u_{14}.
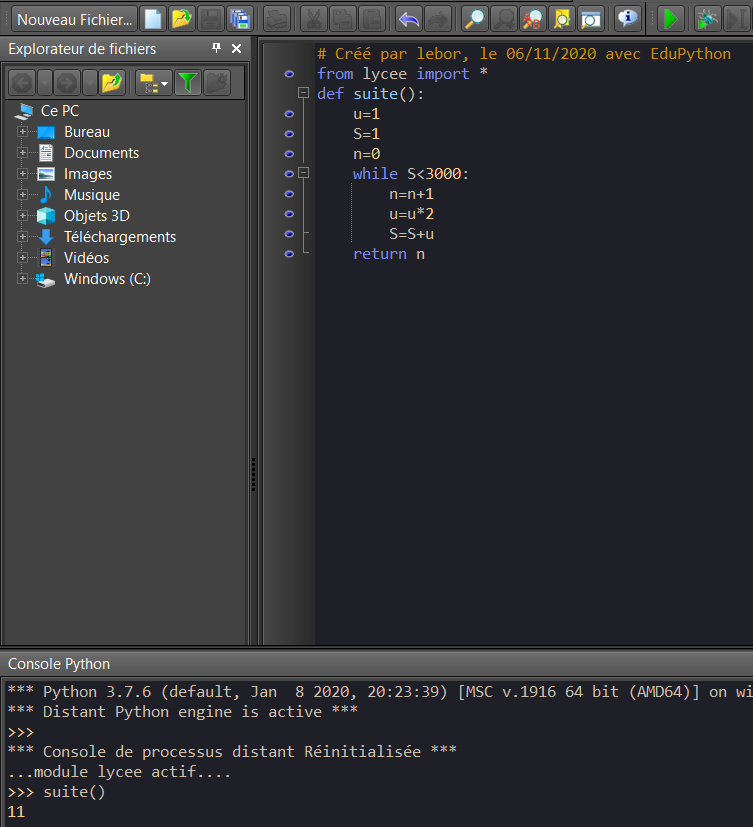
3. Recopier et compléter les pointillés de l’algorithme suivant rédigé en langage Python permettant de déterminer le plus petit entier n tel que la somme des n+1 premiers termes de la suite dépasse 3000.
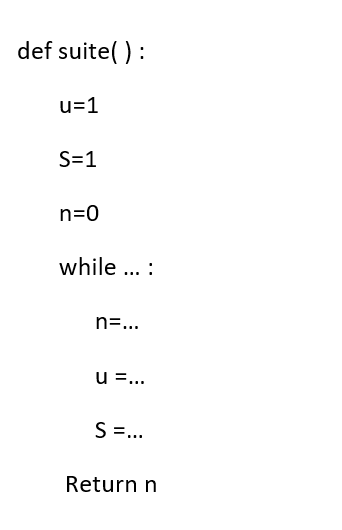
Quelle valeur retourne le programme ?
Partie B
Alain a donné 1 euro à sa petite-fille Cléa pour sa naissance. Ensuite Alain a doublé le montant offert d’une année sur l’autre.
Avec la somme totale versée par son grand-père, combien de scooters d’une valeur de 3000 euros Cléa pourra-t-elle s’offrir à 14 ans ?
Exercice n°3 (calculs de termes, suite géométrique, somme)
Soit (u_n) une suite géométrique de premier terme u_0=2000 et de raison 1.03.
Soit (v_n) une suite définie par v_n=2000+70n.
- Déterminer la forme explicite de la suite géométrique (u_n) . Calculer alors u_5 et u_{10}
2. Calculer u_0 +u_1+u_2+…u_6 .
3. Comparer u_1 et v_1 puis u_{15} et v_{15}.
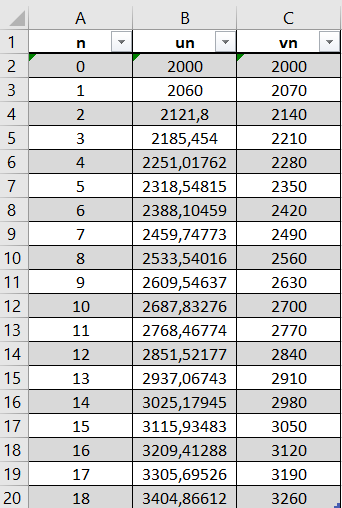
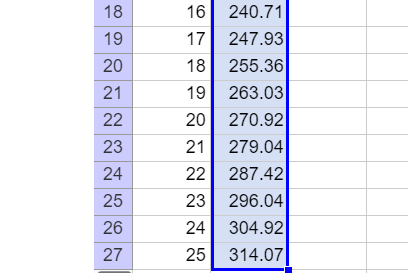
4. Utiliser le tableur ci-dessous pour générer les termes des suites u_n et v_n. Puis déterminer le plus petit entier naturel n tel que u_n>v_n.
Partie B
Ulysse et Victor sont deux amis d’enfance qui sont à la recherche de leur premier emploi.
On propose à Ulysse un emploi rémunéré ainsi 2000 euros par mois la première année et une augmentation tous les ans de 3%.
On propose à Victor un emploi rémunéré ainsi 2000 euros par mois la première année et une augmentation de 70 euros par mois tous les ans.
Au bout de combien d’années, le salaire d’Ulysse sera supérieur au salaire de Victor ?
Exercice n°4 (calculs de termes, variations d’une suite, algorithme)
Soit (u_n) une suite définie pour tout entier naturel n par u_n=\frac{n}{2n+1}
- Calculer u_{0}, u_{1}, u_{2} et u_{99}.
2.a. Exprimer u_{n+1} en fonction de n.
2.b. Montrer que u_{n+1}-u_n=\frac{1}{(2n+3)(2n+1)}.
2.c. En déduire le sens de variation de la suite (u_n).
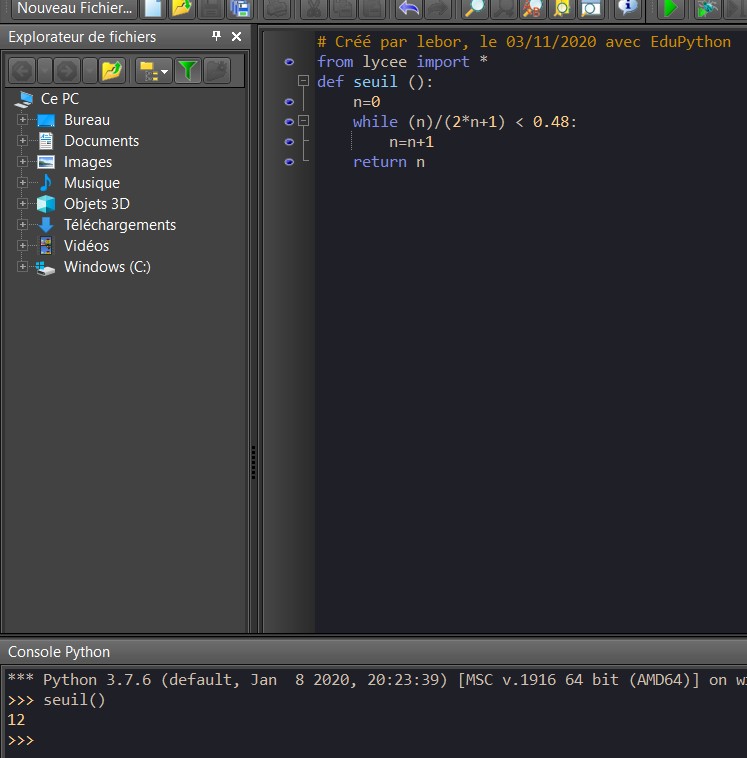
3. Recopier et compléter sur la copie le programme Python suivant pour qu’il permette de déterminer le plus petit entier n tel que u_n<0.48.
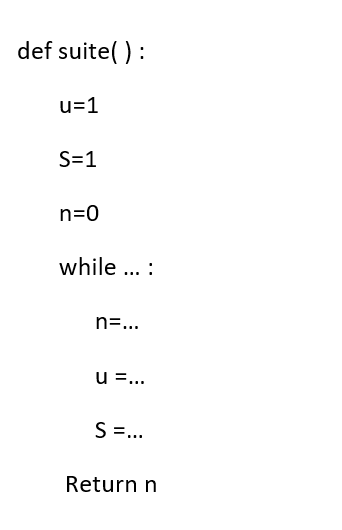
Exercice n°5 (calculs de termes, suite géométrique, somme, algorithme)
Soit (u_n) une suite définie par u_0=300 et u_{n+1}=0.8u_n+50.
Soit (v_n) la suite géométrique de premier terme v_0=-100 et de raison 0.8.
- Calculer u_{1} et u_{2}.
2. Calculer la somme des 20 premiers termes de la suite (v_n).
3. La suite (u_n) est-elle arithmétique ? La suite (u_n) est-elle géométrique ?
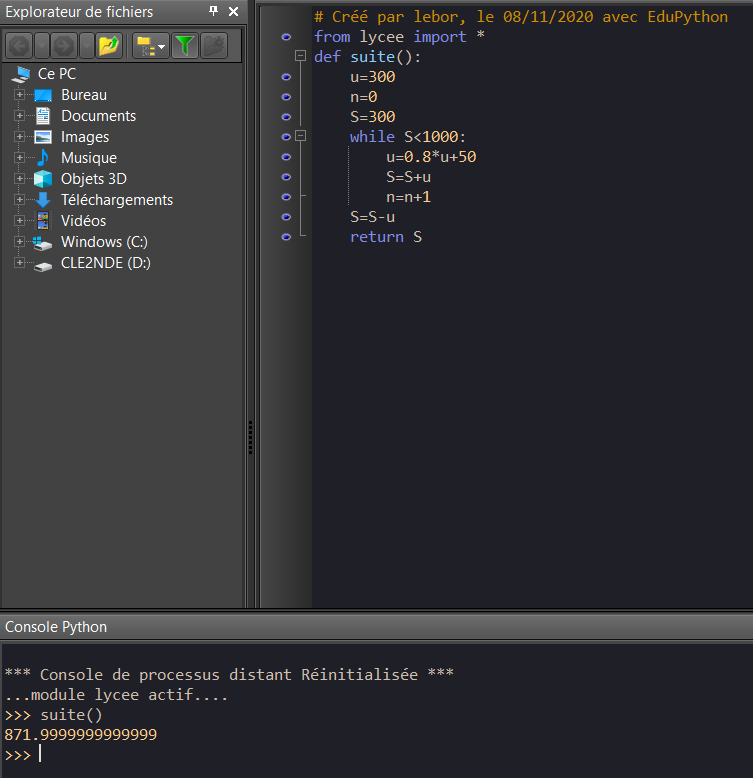
4. Quelle valeur est retournée par cet algorithme. Interpréter ce résultat dans le contexte de l’exercice.
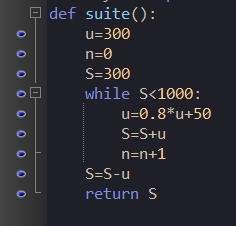
5. On admet que u_n=v_n+250. Calculer u_{20}.
Exercice n°6 (calculs de termes, somme, algorithme)
Sur le site Math’O Karé, on réfléchit à un projet de page sur les réseaux sociaux pour les lycéens.
Le nombre de visites estimé la première semaine est de 150. Ce nombre augmenterait de 3% chaque semaine.
On souhaiterait obtenir 300 visites par semaine.
On modélise cette situation par une suite (u_n) où u_n représente le nombre de visionnage durant la nième semaine . On aura u_0=150.
- Calculer u_{1} et u_{2}.
2. Justifier que pour tout entier n, u_n=150\times 1.03^n.
3. A partir de combien de semaines le nombre de visites sera-t-il supérieur à 300 ? Pour répondre à cette question , utiliser le tableur géogébra ci-dessous.
4. Voici un algorithme écrit en langage Python.
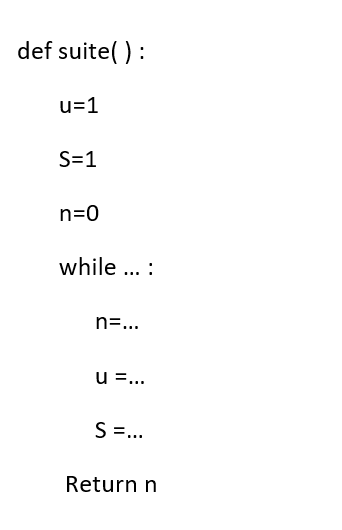
Faire une phrase en langue française pour expliquer ce que fait cet algorithme. Sans le faire tourner, déterminer la valeur qu’il affiche.
5. On pose pour tout entier naturel n, S_n=u_0 +u_1+u_2+…u_n.
Montrer que l’on a S_n=5000(1.03^{n+1}-1). Puis en déduire le nombre de visionnages au bout de 52 semaines.
Exercice n°7 (calculs de termes, suite géométrique)
Dans un laboratoire, on cultive des bactéries artificielles.
Le premier jour de l’étude, la culture compte 6000 cellules.
Un test mené sur cette culture prouve que 15 % des cellules disparaissent chaque jour. On décide alors d’ajouter 3000 cellules chaque jour dans la culture.
On note u_n le nombre de bactéries présentes dans la culture le jour n. On a alors u_0=6000.
1.a.Calculer u_{1} et u_{2}.
1.b. Montrer que la suite u_n n’est ni géométrique, ni arithmétique.
On admet dans la suite de l’exercice que u_{n+1}=0.85\times u_n+3000
2. On considère la suite v_n définie par v_{n}=u_n-20000.
a. Calculer v_0 et démontrer que la suite (v_n) est géométrique de raison 0.85 .
b. Pour tout entier naturel n, exprimer v_n en fonction de n puis montrer que u_n=-14000\times 0.85^n+20000
3. Est-il correct d’affirmer que le nombre de bactéries contenues dans la culture aura triplé au bout de 4 semaines ?
Exercice n°8 (calculs de termes, algorithme)
Actuellement le taux de mortalité des abeilles est de 30 % par an en moyenne en France.
Un apiculteur possède 200 colonies et compte-tenu du taux de mortalité, il décide de rajouter 42 colonies chaque année pour essayer de stabiliser sa production.
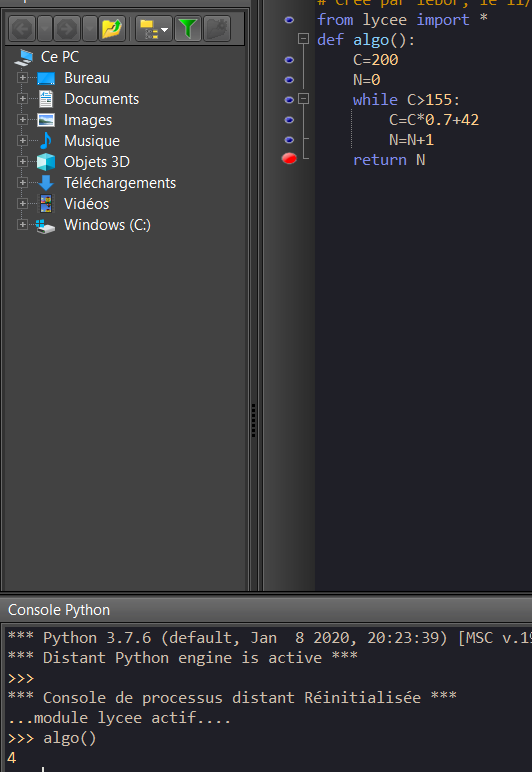
- On donne le programme suivant écrit en langage Python :

a. Faire tourner le programme à la main et compléter le tableau ci-dessous ( arrondir les valeurs C à l’unité près )

b. Quelle est la valeur de N renvoyée par le programme ? Interpréter ce résultat dans le contexte de l’exercice.
On note C_n le nombre de colonies d’abeilles au début de la nième année .
On a alors C_0=200.
On admet que pour tout entier n,
C_{n+1}=0.7C_n+42.
2. La suite C_n est-elle arithmétique ? La suite C_n est-elle géométrique ?
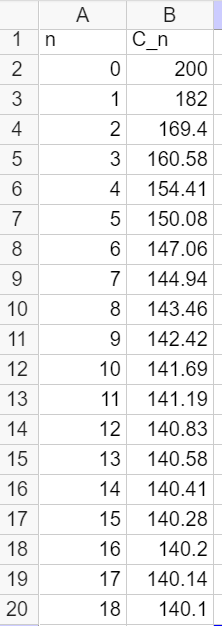
3. On admet que C_n=60\times 0.7^n+140. L’apiculteur pourra-t-il espérer atteindre les 150 colonies dans le futur ? Vous pourrez utiliser la page géogébra ci-dessous en saisissant la bonne formule dans la cellule B2.