Déterminer le signe de f(x)=x^2-4x+4
1.Conjecture graphique :
Pour déterminer graphiquement le signe de f(x)=x^2-4x+4
Je parcours la courbe avec mon index de la gauche vers la droite en disant positif si la courbe de la fonction f est au dessus de l’axe des abscisses et en disant négatif si la courbe de la fonction f est en-dessous de l’axe des abscisses
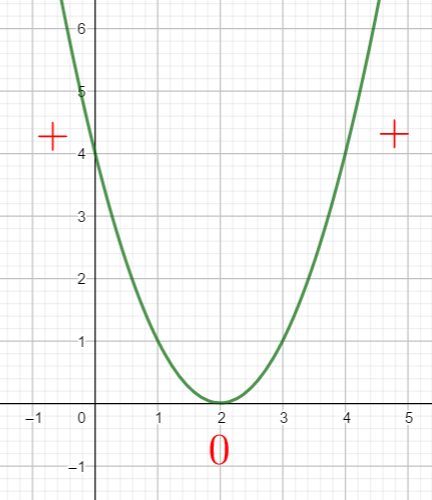
La fonction polynôme est toujours de signe + . Elle s’annule pour la valeur 2 .
2. Etude du signe de f(x)=x^2-4x+4 par le calcul en utilisant le théorème du cours.
J’identifie les coefficients a=1, b=-4 et c=4.
Je calcule \Delta=b²-4ac en remplaçant a,b,c par 1, (-4), 4 .
\Delta=(-4)²-4\times{1}\times{4}\\\Delta=16-16\\\Delta=0comme \Delta=0, ax²+bx+c est toujours du signe de a et s’annule pour x_0=-\frac{b}{2a}
Je calcule x_0=-\frac{b}{2a} en remplaçant a,b par 1, (-4).
x_0=-\frac{(-4)}{2\times{1}}\\x_0=\frac{4}{2}\\x_0=2Je dresse le tableau de signes de la fonction polynôme.
Comme a=1 le signe de a est positif.

3. Vérification avec l’application Calcul formel de géogébra.




