logo

1. Calcul vectoriel et produit scalaire. Cours.

Sommaire

Définition du produit scalaire

Définition

Le produit scalaire d’un vecteur \overrightarrow{u} par un vecteur \overrightarrow{v} est le nombre réel  \overrightarrow{u}.\overrightarrow{v} qui se lit \overrightarrow{u} scalaire \overrightarrow{v}.

Si \overrightarrow{u}=\overrightarrow{AB} et \overrightarrow{v}=\overrightarrow{AC} alors \overrightarrow{u}.\overrightarrow{v}= \overrightarrow{AB}.\overrightarrow{AC}=AB\times AC\times cos(\widehat{BAC})

Si \overrightarrow{u}=\overrightarrow{0} ou \overrightarrow{v}=\overrightarrow{0}  alors \overrightarrow{u}.\overrightarrow{v}=0 .

Exercice n°1

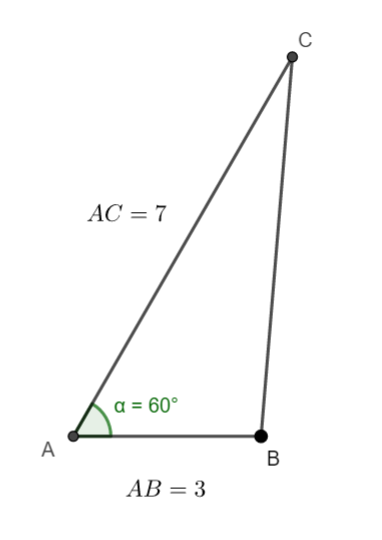
En utilisant la définition, calculer le produit scalaire \overrightarrow{AB}.\overrightarrow{AC}

correction

Exercice n°2

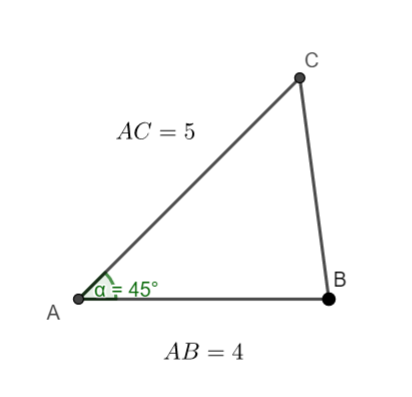
En utilisant la définition, calculer le produit scalaire \overrightarrow{AB}.\overrightarrow{AC}

correction

Exercice n°3

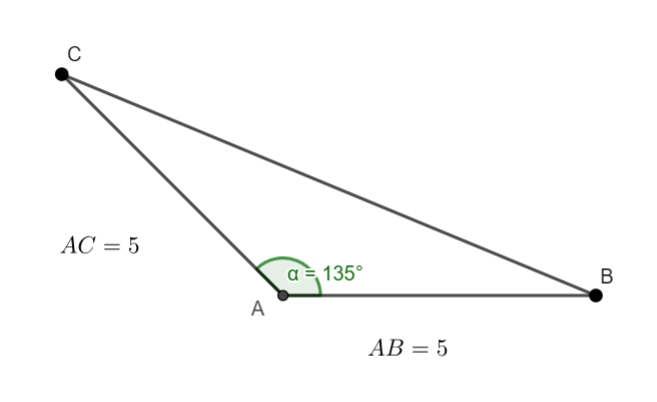
En utilisant la définition, calculer le produit scalaire \overrightarrow{AB}.\overrightarrow{AC}

correction

Le produit scalaire et la projection orthogonale

Propriété

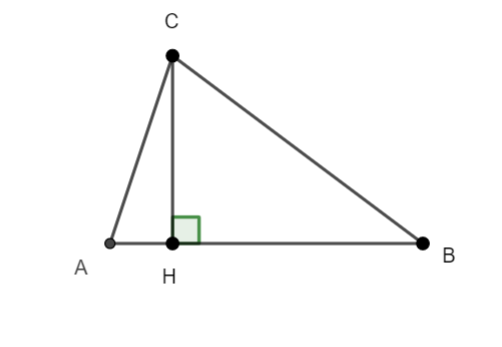
\overrightarrow{u}.\overrightarrow{v}=\overrightarrow{AB}.\overrightarrow{AC}

On projette les points A et C sur la droite (AB).  A projette en A et C se projette en H.

\overrightarrow{u}.\overrightarrow{v}=AB \times AH

car les vecteurs \overrightarrow{AB} et \overrightarrow{AH} ont même sens.

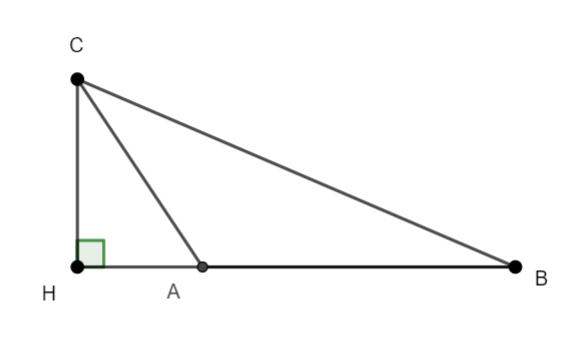
\overrightarrow{u}.\overrightarrow{v}=\overrightarrow{AB}.\overrightarrow{AC}

On projette les points A et C sur la droite (AB).  A projette en A et C se projette en H.

\overrightarrow{u}.\overrightarrow{v}=-AB \times AH

car les vecteurs \overrightarrow{AB} et \overrightarrow{AH} sont de  sens contraire.

Exercice n°4

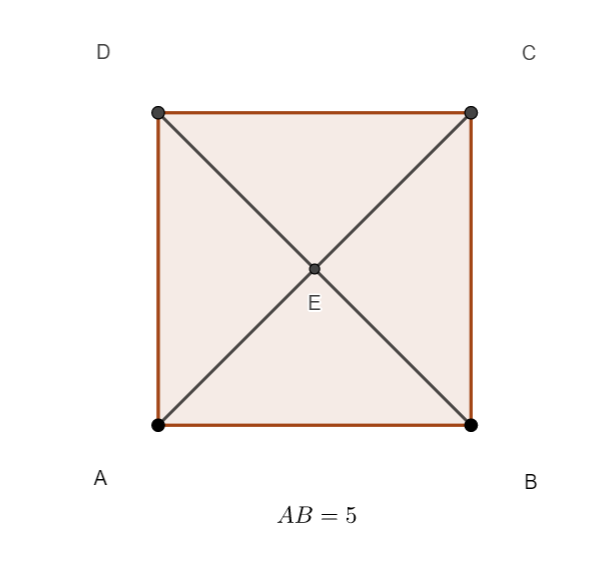
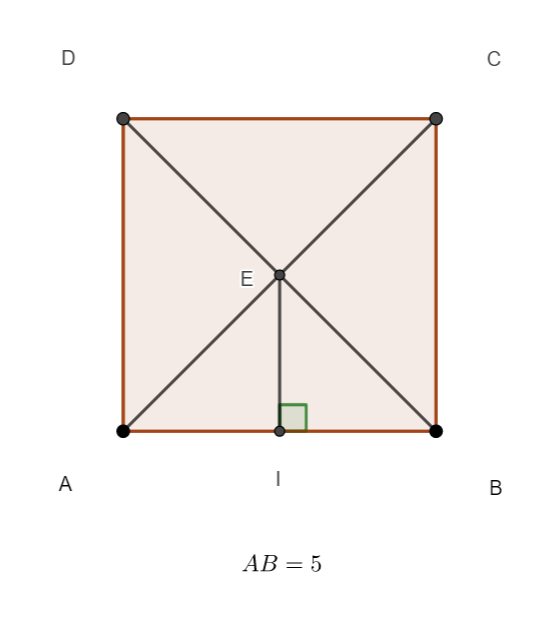
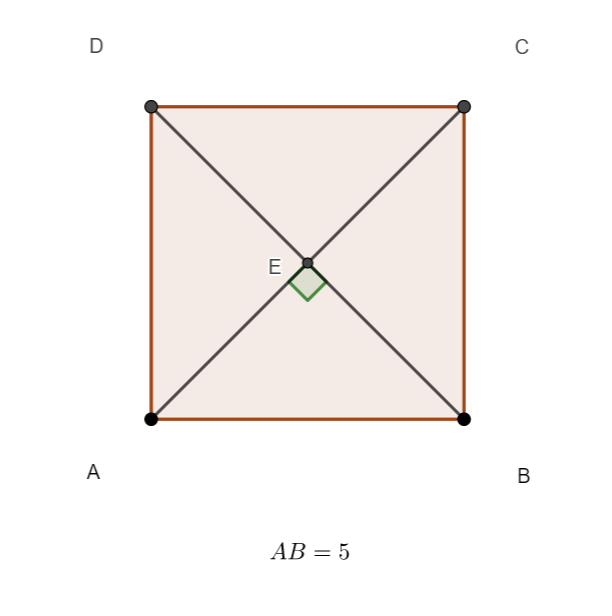
ABCD est un carré de côté 5. 

En utilisant la propriété avec la projection  orthogonale, calculer le produit scalaire \overrightarrow{AB}.\overrightarrow{AE}.

correction

Exercice n°5

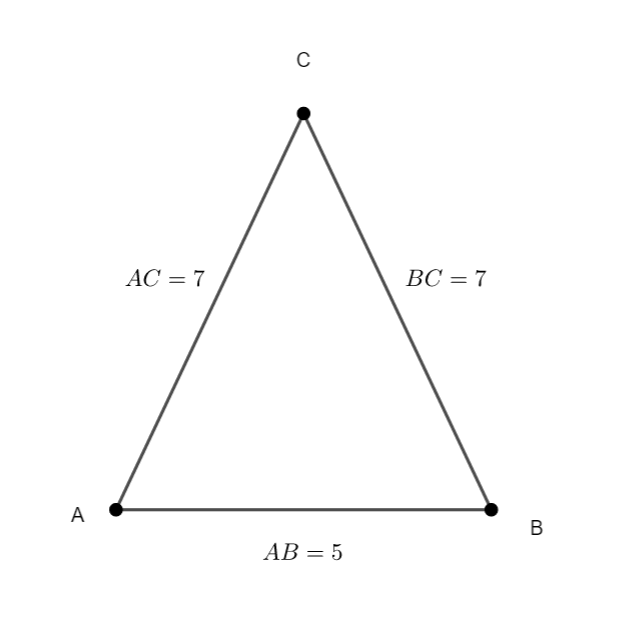
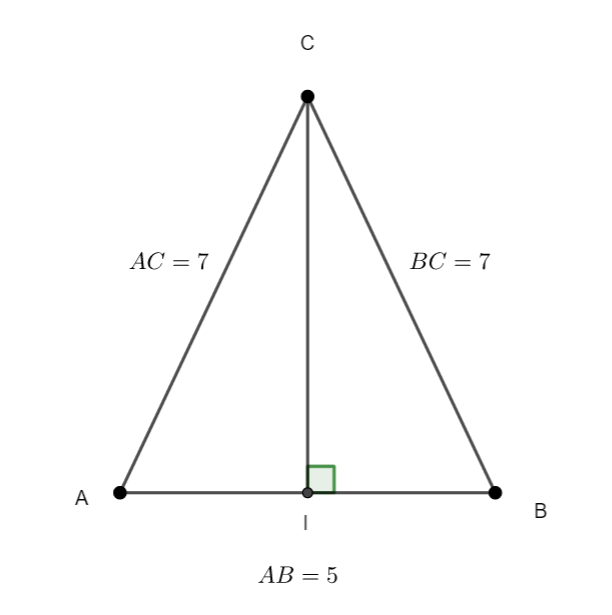
ABC est un triangle isocèle en  C. 

En utilisant la propriété avec la projection  orthogonale, calculer le produit scalaire \overrightarrow{AB}.\overrightarrow{AC}.

correction

Exercice n°6

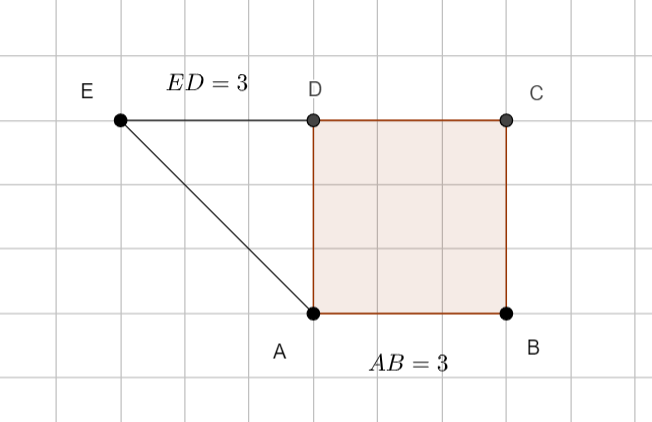
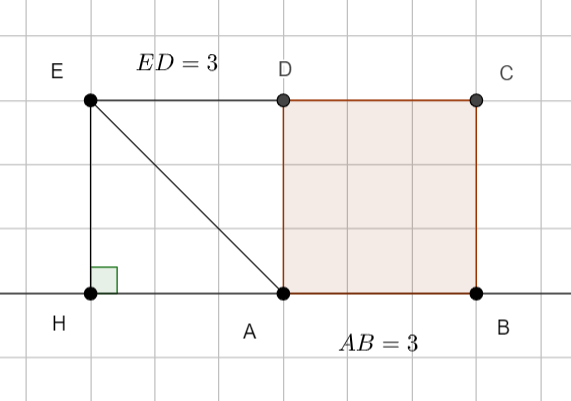
ABCD est un carré de côté 3 et EDA est un triangle isocèle et rectangle en D . 

En utilisant la propriété avec la projection  orthogonale, calculer le produit scalaire \overrightarrow{AB}.\overrightarrow{AE}.

correction

Le produit scalaire et l’orthogonalité

Définition

Dire que deux vecteurs  \overrightarrow{AB} et \overrightarrow{AC} sont orthogonaux signifie que les deux droites   (AB) et (AC) sont perpendiculaires.

Le vecteur nul \overrightarrow{0} est orthogonal à tout vecteur.

Propriété

Pour tous vecteurs   \overrightarrow{u} et \overrightarrow{v} ,  \overrightarrow{u} et \overrightarrow{v} sont orthogonaux équivaut à \overrightarrow{u}.\overrightarrow{v}=0.

Règles de calculs du produit scalaire

Propriétés

Pour tous vecteurs   \overrightarrow{u},  \overrightarrow{v} et \overrightarrow{w}. Pour tout réel  k 

 \overrightarrow{u}.\overrightarrow{v}=\overrightarrow{v}.\overrightarrow{u} 

 \overrightarrow{u}.(\overrightarrow{v}+\overrightarrow{w})=\overrightarrow{u}.\overrightarrow{v}+\overrightarrow{u}.\overrightarrow{w} 

(\overrightarrow{u}+\overrightarrow{v}).\overrightarrow{w}=\overrightarrow{u}.\overrightarrow{w}+\overrightarrow{v}.\overrightarrow{w}

 \overrightarrow{u}.(\overrightarrow{kv})=k(\overrightarrow{u}.\overrightarrow{v})  

 (\overrightarrow{ku}).\overrightarrow{v}=k(\overrightarrow{u}.\overrightarrow{v})  

Exercice n°7

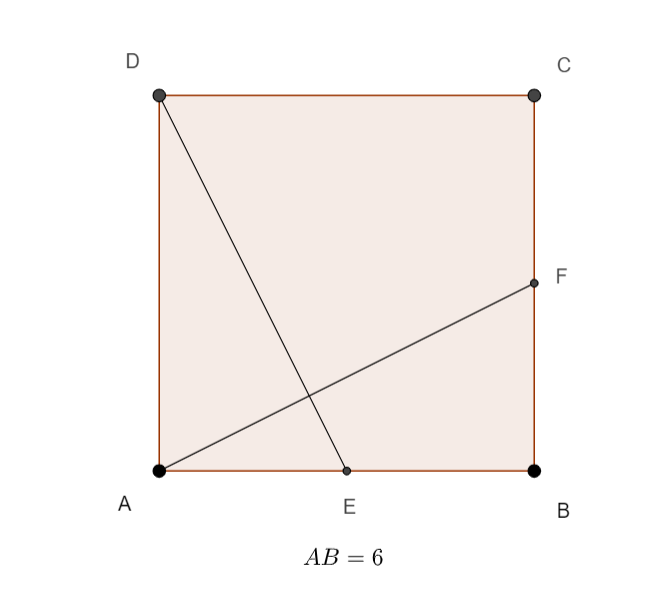
ABCD est un carré de côté 6 , E est le milieu de  [AB] et  F est le milieu de  [BC]. 

L’objectif de cet exercice est de prouver que les droites (DE) et (AF) sont perpendiculaires.

  1. a) A l’aide de la relation de Chasles, compléter les pointillés suivants :\overrightarrow{DE}=\overrightarrow{DA}+…
correction
  1. b) A l’aide de la relation de Chasles, compléter les pointillés suivants :\overrightarrow{AF}=…+\overrightarrow{BF}
correction
  1. c) En utilisant les questions précédentes et les propriétés de calcul, montrer que
\overrightarrow{DE}.\overrightarrow{AF}=\overrightarrow{DA}.\overrightarrow{AB}+\overrightarrow{DA}.\overrightarrow{BF}+\overrightarrow{AE}.\overrightarrow{AB}+\overrightarrow{AE}.\overrightarrow{BF}
correction

2.a) Calculer \overrightarrow{DA}.\overrightarrow{AB} en utilisant le fait qu’ils sont orthogonaux.

correction

2.b) En utilisant la propriété avec la projection  orthogonale, calculer le produit scalaire \overrightarrow{DA}.\overrightarrow{BF}.

correction

2.c) En utilisant la définition, calculer le produit scalaire \overrightarrow{AE}.\overrightarrow{AB}.

correction

2.d) Calculer \overrightarrow{AE}.\overrightarrow{BF} en utilisant le fait qu’ils sont orthogonaux.

correction

3) A l’aide des questions 1 et 2, calculer le produit scalaire  \overrightarrow{DE}.\overrightarrow{AF}. Que peut-on en déduire pour les droites (DE) et (AF) ?

correction

Expression analytique du produit scalaire 

Activité d’approche

Partie 1 : voici la base (\overrightarrow{i};\overrightarrow{j}) ci-dessous.

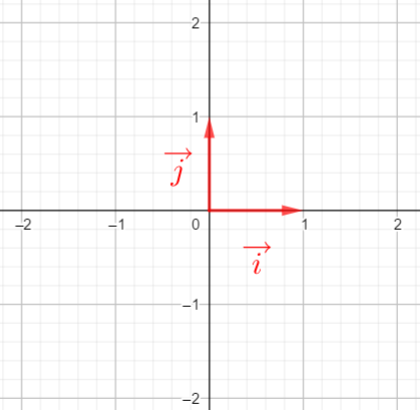
Calculer les produits scalaires suivants : \overrightarrow{i}.\overrightarrow{i}, \overrightarrow{i}.\overrightarrow{j} et \overrightarrow{j}.\overrightarrow{j}

correction

Partie 2 : expression analytique de \overrightarrow{u}.\overrightarrow{v}

Soient \overrightarrow{u}(x;y) et \overrightarrow{v}(x’;y’) dans une base \overrightarrow{i};\overrightarrow{j}.

  1. En remplaçant \overrightarrow{u} par (x\overrightarrow{i}+y\overrightarrow{j}) et \overrightarrow{v} par (x’\overrightarrow{i}+y’\overrightarrow{j}), montrer que 
\overrightarrow{u}.\overrightarrow{v}=xx’\overrightarrow{i}^2+xy’\overrightarrow{i}.\overrightarrow{j}+yx’\overrightarrow{j}.\overrightarrow{i}+yy’\overrightarrow{j}^2
correction

2. En utilisant les résultats de la partie 1, finir le calcul de \overrightarrow{u}.\overrightarrow{v}.

correction

Propriété 

Soient \overrightarrow{u}(x;y) et \overrightarrow{v}(x’;y’) dans une base (\overrightarrow{i};\overrightarrow{j})

 \overrightarrow{u}.\overrightarrow{v}=xx’+yy’

Exercice n°8 

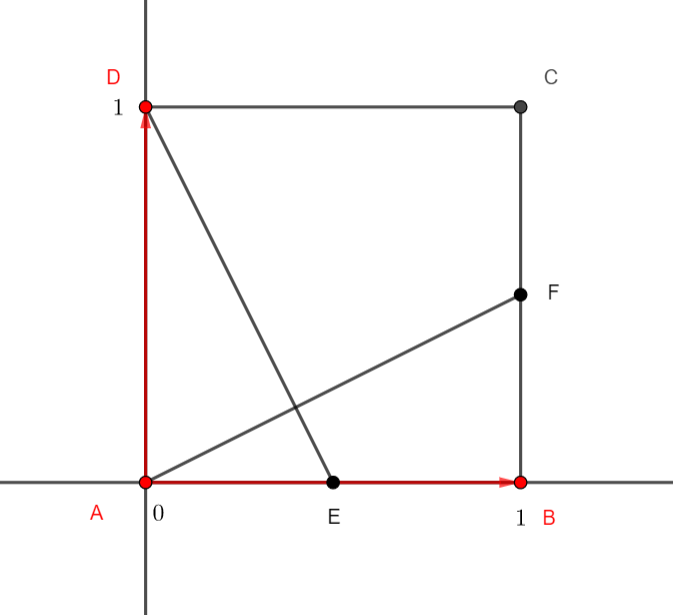
On se propose de montrer que les diagonales d’un carré sont perpendiculaires

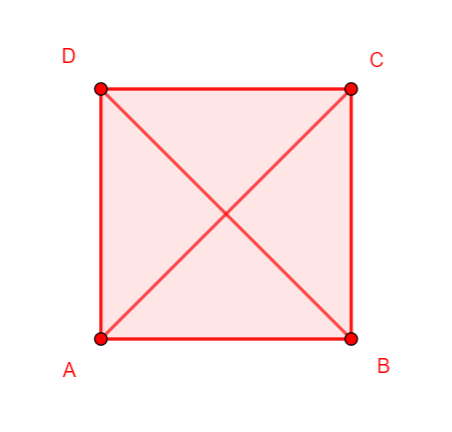
On choisit le repère orthonormé (A;\overrightarrow{AB}; \overrightarrow{AD}). C’est-à-dire que A(0;0), B(1;0) et D(0;1)

1.Déterminer graphiquement les coordonnées du point C.

correction

2.Déterminer par le calcul les coordonnées des vecteurs \overrightarrow{AC} et \overrightarrow{BD}.

correction coordonnées du vecteur \overrightarrow{AC}
correction coordonnées du vecteur \overrightarrow{BD}

3.Calculer le produit scalaire \overrightarrow{AC}.\overrightarrow{BD}. En déduire la position des droites (AC) et (BD).

correction

Exercice n°9 (version de l’exercice n°7 en utilisant le langage des coordonnées )

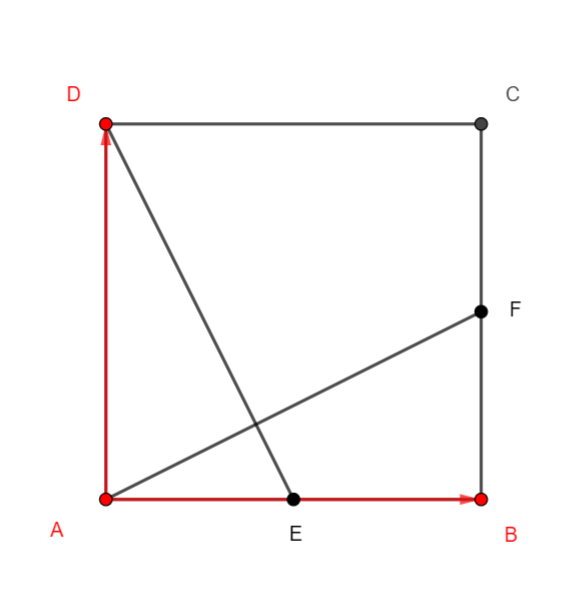
On choisit le repère orthonormé (A;\overrightarrow{AB}; \overrightarrow{AD}). C’est-à-dire que A(0;0), B(1;0) et D(0;1)

1.Déterminer graphiquement les coordonnées des points E et F.

correction

2.Déterminer par le calcul les coordonnées des vecteurs \overrightarrow{DE} et \overrightarrow{AF}.

correction coordonnées du vecteur \overrightarrow{DE}
correction coordonnées du vecteurs \overrightarrow{AF}

3.Calculer le produit scalaire \overrightarrow{DE}.\overrightarrow{AF}. En déduire la position des droites (DE) et (AF).

correction

Le produit scalaire et les normes

Propriété n°1 

\overrightarrow{u}^2 = ||\overrightarrow{u}||^2

Démonstration :

\overrightarrow{u}^2 = \overrightarrow{u}.\overrightarrow{u}\\\hspace{0.55cm} = ||\overrightarrow{u}||.||\overrightarrow{u}||.cos(0)  d’après la définition du produit scalaire.

\hspace{0.55cm}= ||\overrightarrow{u}||.||\overrightarrow{u}||\\\hspace{0.55cm} = ||\overrightarrow{u}||^2

Exercice n°10 : formule de la médiane

Le but de cet exercice est de montrer la propriété suivante.

A et B sont deux points du plan et I est le milieu de [AB].

Pour tout point M du plan, on a 

MA^2+MB^2=2MI^2+\frac{AB^2}{2}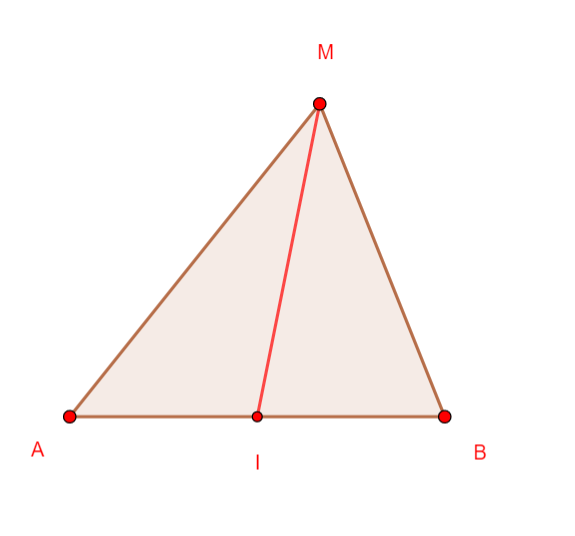

En utilisant la propriété n°1 ci-dessus, on peut écrire :

MA^2+MB^2=\overrightarrow{MA}^2+\overrightarrow{MB}^2

En utilisant la relation de Chasles , on peut écrire \overrightarrow{MA}^2=(\overrightarrow{MI}+\overrightarrow{IA})^2.

1.Développer (\overrightarrow{MI}+\overrightarrow{IA})^2

correction

En utilisant la relation de Chasles , on peut écrire \overrightarrow{MB}^2=(\overrightarrow{MI}+\overrightarrow{IB})^2.

2.Développer (\overrightarrow{MI}+\overrightarrow{IB})^2

correction

3.En ajoutant membre à membre les deux égalités précédentes, démontrer que

MA^2+MB^2=2MI^2+\frac{AB^2}{2}.

correction

Propriété n°2 

Pour tous vecteurs \overrightarrow{u} et \overrightarrow{v}.

||\overrightarrow{u}+\overrightarrow{v}||^2=||\overrightarrow{u}||^2+2\overrightarrow{u}.\overrightarrow{v}+||\overrightarrow{v}||^2

||\overrightarrow{u}-\overrightarrow{v}||^2=||\overrightarrow{u}||^2-2\overrightarrow{u}.\overrightarrow{v}+||\overrightarrow{v}||^2

Démonstration 1 :

||\overrightarrow{u}+\overrightarrow{v}||^2 = (\overrightarrow{u}+\overrightarrow{v})^2 d’après la propriété n°1

\hspace{1.7cm} =\overrightarrow{u}^2+2 \overrightarrow{u}.\overrightarrow{v}+\overrightarrow{v}^2  d’après les règles de calculs précédentes

\hspace{1.7cm} =||\overrightarrow{u}||^2+2 \overrightarrow{u}.\overrightarrow{v}+||\overrightarrow{v}||^2 d’après la propriété n°1

Démonstration 2 :

||\overrightarrow{u}-\overrightarrow{v}||^2 = (\overrightarrow{u}-\overrightarrow{v})^2 d’après la propriété n°1

\hspace{1.7cm} =\overrightarrow{u}^2-2 \overrightarrow{u}.\overrightarrow{v}+\overrightarrow{v}^2  d’après les règles de calculs précédentes

\hspace{1.7cm} =||\overrightarrow{u}||^2-2 \overrightarrow{u}.\overrightarrow{v}+||\overrightarrow{v}||^2 d’après la propriété n°1

Propriété n°3 

Pour tous vecteurs \overrightarrow{u} et \overrightarrow{v}.

\overrightarrow{u}.\overrightarrow{v}=\frac{1}{2}(||\overrightarrow{u}||^2+||\overrightarrow{v}||^2- ||\overrightarrow{u}-\overrightarrow{v}||^2)

\overrightarrow{u}.\overrightarrow{v}=\frac{1}{2}(||\overrightarrow{u}+\overrightarrow{v}||^2)||-||\overrightarrow{u}||^2- ||\overrightarrow{v}||^2)

©2020 – Math’O karé SAS

Calculons le produit scalaire \overrightarrow{AB}.\overrightarrow{AC} à l’aide de la définition.

Je remplace AB par 3, AC par 7 et \widehat{BAC} par 60 dans \overrightarrow{AB}.\overrightarrow{AC}=AB\times AC\times cos(\widehat{BAC}).

\overrightarrow{AB}.\overrightarrow{AC}=3\times 7\times cos(60)

\hspace{1.3cm}=21\times 0.5

\hspace{1.3cm}=10.5

Calculons le produit scalaire \overrightarrow{AB}.\overrightarrow{AC} à l’aide de la définition.

Je remplace AB par 4, AC par 5 et \widehat{BAC} par 45 dans \overrightarrow{AB}.\overrightarrow{AC}=AB\times AC\times cos(\widehat{BAC}).

\overrightarrow{AB}.\overrightarrow{AC}=4\times 5\times cos(45)

\hspace{1.3cm}=20\times 0.7

\hspace{1.3cm}=14.14

 

Calculons le produit scalaire \overrightarrow{AB}.\overrightarrow{AC} à l’aide de la définition.

Je remplace AB par 5, AC par 5 et \widehat{BAC} par 135 dans \overrightarrow{AB}.\overrightarrow{AC}=AB\times AC\times cos(\widehat{BAC}).

\overrightarrow{AB}.\overrightarrow{AC}=5\times 5\times cos(135)

\hspace{1.3cm}=25\times (-0.7)

\hspace{1.3cm}=-17.68

Pour calculer le produit scalaire \overrightarrow{AB}.\overrightarrow{AE} à l’aide de la propriété avec la projection orthogonale, il y a deux façons de procéder. Parfois les deux fonctionnent comme c’est le cas ici et je vous donne les deux méthodes. On constate que la première est la plus pertinente car plus rapide. Parfois il n’y a qu’une méthode qui permet de conclure.

Méthode n°1 : Calculons le produit scalaire \overrightarrow{AB}.\overrightarrow{AE} à l’aide de la propriété avec la projection orthogonale.

On projette les points A et E du 2ème vecteur \overrightarrow{AE} sur la droite (AB) qui correspond au 1er vecteur \overrightarrow{AB}.

A se projette en A et E se projette en I qui est le milieu du segment  [AB]

\overrightarrow{AB}.\overrightarrow{AE}=AB\times AI car \overrightarrow{AB} et \overrightarrow{AI} ont même sens.

\hspace{1.3cm}=AB\times \frac{AB}{2} car I  est le milieu du segment  [AB]

\hspace{1.3cm}=5\times \frac{5}{2}

\hspace{1.3cm}= \frac{25}{2}

Méthode n°2 : Calculons le produit scalaire \overrightarrow{AE}.\overrightarrow{AB} à l’aide de la propriété avec la projection orthogonale ( ce qui revient au  même par rapport à la méthode n°1 car \overrightarrow{u}.\overrightarrow{v}=\overrightarrow{v}.\overrightarrow{u}

On projette les points A et B du 2ème vecteur \overrightarrow{AB} sur la droite (AE) qui correspond au 1er vecteur \overrightarrow{AE}.

A se projette en A et B se projette en E qui est le milieu du segment  [AC]

\overrightarrow{AE}.\overrightarrow{AB}=AE\times AE car \overrightarrow{AE} et \overrightarrow{AE} ont même sens.

\hspace{1.3cm}=\frac{AC}{2}\times \frac{AC}{2} car E  est le milieu du segment  [AC]

\hspace{1.3cm}= \frac{AC^2}{4}

\hspace{1.3cm}= \frac{AB^2+BC^2}{4} d’après Pythagore.

\hspace{1.3cm}= \frac{5^2+5^2}{4}

\hspace{1.3cm}= \frac{25+25}{4}

\hspace{1.3cm}= \frac{50}{4}

\hspace{1.3cm}= \frac{25}{2}

 

Pour calculer le produit scalaire \overrightarrow{AB}.\overrightarrow{AC} à l’aide de la propriété avec la projection orthogonale, il y a deux façons de procéder. Parfois les deux fonctionnent ce n’est pas le cas ici , seule la première méthode permet de conclure.

Méthode n°1 : Calculons le produit scalaire \overrightarrow{AB}.\overrightarrow{AC} à l’aide de la propriété avec la projection orthogonale.

On projette les points A et C du 2ème vecteur \overrightarrow{AC} sur la droite (AB) qui correspond au 1er vecteur \overrightarrow{AB}.

A se projette en A et C se projette en I qui est le milieu du segment  [AB]

\overrightarrow{AB}.\overrightarrow{AC}=AB\times AI car \overrightarrow{AB} et \overrightarrow{AI} ont même sens.

\hspace{1.3cm}=AB\times \frac{AB}{2} car I  est le milieu du segment  [AB]

\hspace{1.3cm}=5\times \frac{5}{2}

\hspace{1.3cm}= \frac{25}{2}

Méthode n°2 : Calculons le produit scalaire \overrightarrow{AC}.\overrightarrow{AB} à l’aide de la propriété avec la projection orthogonale ( ce qui revient au  même par rapport à la méthode n°1 car \overrightarrow{u}.\overrightarrow{v}=\overrightarrow{v}.\overrightarrow{u}

On projette les points A et B du 2ème vecteur \overrightarrow{AB} sur la droite (AC) qui correspond au 1er vecteur \overrightarrow{AC}.

A se projette en A et B se projette en un point inconnu pour lequel on ne pourra pas calculer sa distance entre lui et A.

Cette méthode ne fonctionne pas.

 

Pour calculer le produit scalaire \overrightarrow{AB}.\overrightarrow{AE} à l’aide de la propriété avec la projection orthogonale, il y a deux façons de procéder. Parfois les deux fonctionnent ce n’est pas le cas ici , seule la première méthode permet de conclure.

Méthode n°1 : Calculons le produit scalaire \overrightarrow{AB}.\overrightarrow{AE} à l’aide de la propriété avec la projection orthogonale.

On projette les points A et E du 2ème vecteur \overrightarrow{AE} sur la droite (AB) qui correspond au 1er vecteur \overrightarrow{AB}.

A se projette en A et E se projette en H qui est le symétrique de B par rapport au point A.

\overrightarrow{AB}.\overrightarrow{AE}=-AB\times AH car \overrightarrow{AB} et \overrightarrow{AH} sont de sens contraire.

\hspace{1.3cm}=-3\times 3 

\hspace{1.3cm}=-9

Méthode n°2 : Calculons le produit scalaire \overrightarrow{AE}.\overrightarrow{AB} à l’aide de la propriété avec la projection orthogonale ( ce qui revient au  même par rapport à la méthode n°1 car \overrightarrow{u}.\overrightarrow{v}=\overrightarrow{v}.\overrightarrow{u})

On projette les points A et B du 2ème vecteur \overrightarrow{AB} sur la droite (AE) qui correspond au 1er vecteur \overrightarrow{AE}.

A se projette en A et B se projette en un point inconnu pour lequel on ne pourra pas calculer sa distance entre lui et A.

Cette méthode ne fonctionne pas.

 

En utilisant la relation de Chasles, on peut écrire :

\overrightarrow{DE}=\overrightarrow{DA}+\overrightarrow{AE}.

En utilisant la relation de Chasles, on peut écrire :

\overrightarrow{AF}=\overrightarrow{AB}+\overrightarrow{BF}.

On veut montrer l’égalité suivante :

\overrightarrow{DE}.\overrightarrow{AF}=\overrightarrow{DA}.\overrightarrow{AB}+\overrightarrow{DA}.\overrightarrow{BF}+\overrightarrow{AE}.\overrightarrow{AB}+\overrightarrow{AE}.\overrightarrow{BF}

On va partir du membre de gauche, le transformer en utilisant les 2 questions précédentes et arriver au membre de droite.

\overrightarrow{DE}.\overrightarrow{AF}=(\overrightarrow{DA}+\overrightarrow{AE}) (\overrightarrow{AB}+\overrightarrow{BF})

On va utiliser la distributivité de la multiplication par rapport à l’addition pour développer ce produit.

\hspace{1.3cm}=\overrightarrow{DA}.\overrightarrow{AB}+\overrightarrow{DA}.\overrightarrow{BF}+\overrightarrow{AE}.\overrightarrow{AB}+\overrightarrow{AE}.\overrightarrow{BF}

Les côtés [DA] et [AB] sont deux côtés consécutifs d’un carré donc ils sont perpendiculaires, donc :

\overrightarrow{DA}.\overrightarrow{AB}=0

Pour calculer \overrightarrow{DA}.\overrightarrow{BF} , on va utiliser la projection et on va projeter les points A et D du vecteur \overrightarrow{DA} sur la droite (BF).

A se projette en  B et D se projette en  C.

\overrightarrow{DA}.\overrightarrow{BF}=-CB\times BF car les vecteurs \overrightarrow{CB} et \overrightarrow{BF} sont de sens contraire.

\hspace{1.4cm}=-6\times 3\\\hspace{1.4cm}=-18

Pour calculer \overrightarrow{AE}.\overrightarrow{AB} , on va utiliser la projection et on va projeter les points A et E du vecteur \overrightarrow{AE} sur la droite (AB).

A se projette en  A et E se projette en  E.

\overrightarrow{AE}.\overrightarrow{AB}=AE\times AB car les vecteurs \overrightarrow{AE} et \overrightarrow{AB} ont même sens.

\hspace{1.4cm}=3\times 6\\\hspace{1.4cm}=18

Les côtés [AB] et [BC] sont deux côtés consécutifs d’un carré donc ils sont perpendiculaires, donc les droites (AE) et (BF) sont perpendiculaires. Donc :

\overrightarrow{AE}.\overrightarrow{BF}=0

On va utiliser ce qu’on a obtenu dans la question 1.c

\overrightarrow{DE}.\overrightarrow{AF}=\overrightarrow{DA}.\overrightarrow{AB}+\overrightarrow{DA}.\overrightarrow{BF}+\overrightarrow{AE}.\overrightarrow{AB}+\overrightarrow{AE}.\overrightarrow{BF}

On remplace ensuite les produits salaires par les valeurs qu’on a obtenues à la question 2.

On remplace \overrightarrow{DA}.\overrightarrow{AB} par 0.

On remplace \overrightarrow{DA}.\overrightarrow{BF} par -18.

On remplace \overrightarrow{AE}.\overrightarrow{AB} par 18.

On remplace \overrightarrow{AE}.\overrightarrow{BF} par 0.

\overrightarrow{DE}.\overrightarrow{AF}=\overrightarrow{DA}.\overrightarrow{AB}+\overrightarrow{DA}.\overrightarrow{BF}+\overrightarrow{AE}.\overrightarrow{AB}+\overrightarrow{AE}.\overrightarrow{BF}\\\hspace{1.4cm}=0-18+18+0\\\hspace{1.4cm}=0

Donc les droites (DE) et (AF) sont perpendiculaires.

 

\overrightarrow{i}.\overrightarrow{i}=||\overrightarrow{i}||\times ||\overrightarrow{i}|| \times cos(0)\\ \hspace{0.85cm}=1\times 1 \times 1\\ \hspace{0.85cm}=1\\\overrightarrow{i}.\overrightarrow{j}=||\overrightarrow{i}||\times ||\overrightarrow{j}|| \times cos(\frac{\pi}{2})\\ \hspace{0.85cm}=1\times 1 \times 0\\ \hspace{0.85cm}=0

Remarque : \overrightarrow{j}.\overrightarrow{i}=0 aussi.

\overrightarrow{j}.\overrightarrow{j}=||\overrightarrow{j}||\times ||\overrightarrow{j}|| \times cos(0)\\ \hspace{0.85cm}=1\times 1 \times 1\\ \hspace{0.85cm}=1\\

Pour montrer l’égalité suivante : \overrightarrow{u}.\overrightarrow{v}=xx’\overrightarrow{i}^2+xy’\overrightarrow{i}.\overrightarrow{j}+yx’\overrightarrow{j}.\overrightarrow{i}+yy’\overrightarrow{j}^2, on part du membre de gauche et on le transforme pour obtenir le membre de droite.

Tout d’abord on remplace \overrightarrow{u} par (x\overrightarrow{i}+y\overrightarrow{j}) et \overrightarrow{v} par (x’\overrightarrow{i}+y’\overrightarrow{j}).

\overrightarrow{u}.\overrightarrow{v}=(x\overrightarrow{i}+y\overrightarrow{j}).(x’\overrightarrow{i}+y’\overrightarrow{j})

Ensuite on développe le produit en utilisant la distributivité de la multiplication par rapport à l’addition.

\hspace{0.85cm}=xx’\overrightarrow{i}^2+xy’\overrightarrow{i}.\overrightarrow{j}+yx’\overrightarrow{j}.\overrightarrow{i}+yy’\overrightarrow{j}^2

On a montré précédemment que :

\overrightarrow{u}.\overrightarrow{v}=xx’\overrightarrow{i}^2+xy’\overrightarrow{i}.\overrightarrow{j}+yx’\overrightarrow{j}.\overrightarrow{i}+yy’\overrightarrow{j}^2

D’après la  question 1) on peut remplacer \overrightarrow{i}.\overrightarrow{i} par 1  , \overrightarrow{i}.\overrightarrow{j} par 0, \overrightarrow{j}.\overrightarrow{i} par 0 et \overrightarrow{j}.\overrightarrow{j} par 1\\\overrightarrow{u}.\overrightarrow{v}=xx’\times 1+xy’\times 0+yx’\times 0+yy’\times 1\\\hspace{0.85cm}=xx’+yy’

Pour déterminer les coordonnées du vecteur \overrightarrow{AC}.

Je repère les coordonnées des points A et C.

\hspace{1.8cm}x_{A}\hspace{0.2cm}y_{A}\hspace{2.2cm}x_{C}\hspace{0.2cm}y_{C}

\hspace{1.8cm}A(0;0)\hspace{2cm}C(1;1)

J’écris la formule : \overrightarrow{AC}(x_{C}-x_{A};y_{C}-y_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AC}(1-0;1-0)

\overrightarrow{AC}(1;1)

 

Pour déterminer les coordonnées du vecteur \overrightarrow{BD}.

Je repère les coordonnées des points B et D.

\hspace{1.8cm}x_{B}\hspace{0.2cm}y_{B}\hspace{2.2cm}x_{D}\hspace{0.2cm}y_{D}

\hspace{1.8cm}B(1;0)\hspace{2cm}D(0;1)

J’écris la formule : \overrightarrow{BD}(x_{D}-x_{B};y_{D}-y_{B})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{BD}(0-1;1-0)

\overrightarrow{BD}(-1;1)

On a vu que \overrightarrow{AC}(1;1) et que \overrightarrow{BD}(-1;1).

Pour calculer le produit scalaire \overrightarrow{AC}.\overrightarrow{BD}, on va utiliser xx’+yy’ en remplaçant x par 1 , y par 1 , x’ par -1 et y’ par 1.

\overrightarrow{AC}.\overrightarrow{BD}=1\times (-1)+1\times 1

\hspace{1.3cm}=0

Le produit scalaire est nul donc les droites (AC) et (BD) sont perpendiculaires.

Et voici comment démontrer facilement que les diagonales d’un carré sont perpendiculaires.

Quand on choisit de résoudre un problème de géométrie en choisissant un repère, on peut tracer l’axe des abscisses, l’axe des ordonnées et de placer quelques graduations sur les axes. 

Pour aller de l’origine au point E, on se déplace horizontalement d’une demi-graduation vers la droite et c’est tout. Donc  E(\frac{1}{2};0).

Pour aller de l’origine au point F, on se déplace horizontalement de 1graduation vers la droite et on monte d’une demi-graduation. Donc  F(1;\frac{1}{2}).

Pour déterminer les coordonnées du vecteur \overrightarrow{DE}.

Je repère les coordonnées des points D et E.

\hspace{1.8cm}x_{D}\hspace{0.2cm}y_{D}\hspace{2.2cm}x_{E}\hspace{0.2cm}y_{E}

\hspace{1.8cm}D(0;1)\hspace{2cm}E(\frac{1}{2};0)

J’écris la formule : \overrightarrow{DE}(x_{E}-x_{D};y_{E}-y_{D})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{DE}(\frac{1}{2}-0;0-1)\\\overrightarrow{DE}(\frac{1}{2};-1)

 

Pour déterminer les coordonnées du vecteur \overrightarrow{AF}.

Je repère les coordonnées des points A et F.

\hspace{1.8cm}x_{A}\hspace{0.2cm}y_{A}\hspace{2.2cm}x_{F}\hspace{0.2cm}y_{F}

\hspace{1.8cm}A(0;0)\hspace{2cm}F(1;\frac{1}{2})

J’écris la formule : \overrightarrow{AF}(x_{F}-x_{A};y_{F}-y_{A})

On prend soin de remplacer les lettres par les bons nombres. ATTENTION : quand on remplace une lettre par un nombre négatif, on le met entre parenthèses.

\overrightarrow{AF}(1-0;\frac{1}{2}-0)\\\overrightarrow{AF}(1;\frac{1}{2})

On a vu que \overrightarrow{DE}(\frac{1}{2};-1) et que \overrightarrow{AF}(1;\frac{1}{2}).

Pour calculer le produit scalaire \overrightarrow{DE}.\overrightarrow{AF}, on va utiliser xx’+yy’ en remplaçant x par \frac{1}{2} , y par -1 , x’ par 1 et y’ par \frac{1}{2}.

\overrightarrow{DE}.\overrightarrow{AF}=\frac{1}{2}\times 1+(-1)\times \frac{1}{2}

\hspace{1.3cm}=\frac{1}{2}-\frac{1}{2}

\hspace{1.3cm}=0

Le produit scalaire est nul donc les droites (DE) et (AF) sont perpendiculaires.

 

Pour développer (\overrightarrow{MI}+\overrightarrow{IA})^2 on va utiliser l’identité remarquable (a+b)^2=a^2+2ab+b^2.

(\overrightarrow{MI}+\overrightarrow{IA})^2=\overrightarrow{MI}^2+2\overrightarrow{MI}.\overrightarrow{IA}+\overrightarrow{IA}^2

J’utilise la propriété n°1  \overrightarrow{u}^2=||\overrightarrow{u}||^2

\hspace{1.8cm}=MI^2+2\overrightarrow{MI}.\overrightarrow{IA}+IA^2

Comme I est le milieu de [AB] alors IA=\frac{AB}{2}.

\hspace{1.8cm}=MI^2+2\overrightarrow{MI}.\overrightarrow{IA}+(\frac{AB}{2})^2

\hspace{1.8cm}=MI^2+2\overrightarrow{MI}.\overrightarrow{IA}+\frac{AB^2}{4}

Pour développer (\overrightarrow{MI}+\overrightarrow{IB})^2 on va utiliser l’identité remarquable (a+b)^2=a^2+2ab+b^2.

(\overrightarrow{MI}+\overrightarrow{IB})^2=\overrightarrow{MI}^2+2\overrightarrow{MI}.\overrightarrow{IB}+\overrightarrow{IB}^2

J’utilise la propriété n°1  \overrightarrow{u}^2=||\overrightarrow{u}||^2

\hspace{1.9cm}=MI^2+2\overrightarrow{MI}.\overrightarrow{IB}+IB^2

Comme I est le milieu de [AB] alors IB=\frac{AB}{2}.

\hspace{1.9cm}=MI^2+2\overrightarrow{MI}.\overrightarrow{IB}+(\frac{AB}{2})^2

\hspace{1.9cm}=MI^2+2\overrightarrow{MI}.\overrightarrow{IB}+\frac{AB^2}{4}

Dans la question n°1 on a montré que

MA^2=MI^2+2\overrightarrow{MI}.\overrightarrow{IA}+\frac{AB^2}{4}

Dans la question n°2 on a montré que

MB^2=MI^2+2\overrightarrow{MI}.\overrightarrow{IB}+\frac{AB^2}{4}

On ajoute ces deux égalités membre à membre :

MA^2+MB^2=MI^2+2\overrightarrow{MI}.\overrightarrow{IA}+\frac{AB^2}{4}+MI^2+2\overrightarrow{MI}.\overrightarrow{IB}+\frac{AB^2}{4}

On met 2\overrightarrow{MI}en facteur dans 2\overrightarrow{MI}.\overrightarrow{IA}+2\overrightarrow{MI}.\overrightarrow{IB}

MA^2+MB^2=2MI^2+2\overrightarrow{MI}(\overrightarrow{IA}+\overrightarrow{IB})+\frac{AB^2}{4}+\frac{AB^2}{4}

Comme Iest le milieu de [AB] ,  \overrightarrow{IA}+\overrightarrow{IB}=\overrightarrow{0}

MA^2+MB^2=2MI^2+2\overrightarrow{MI}.\overrightarrow{0}+\frac{2AB^2}{4}

MA^2+MB^2=2MI^2+\frac{AB^2}{2}

Réponse:

\overrightarrow{DC}=\overrightarrow{HG}.

Résoudre graphiquement f(x)=1

C’est une autre façon de demander de déterminer graphiquement les antécédents de 1.

Je place 1 sur l’axe des ordonnées, je trace alors la parallèle à l’axe des abscisses passant par 1 toute entière. Je repère les points d’intersection avec la courbe. Les abscisses de ces points sont les antécédents de 1.

Les antécédents sont -2 et 2.

Donc S=\{-2;2\}

Remarque : comme on demande de résoudre une équation, il faut écrire ainsi l’ensemble des solutions.